错位散斑检测灵敏度的定量分析与优化策略

1. 缺陷的力学模型：将不可见损伤理论化

在航空航天工程中，复合材料蜂窝夹层结构因其轻质高强的特性而被广泛应用。然而，其结构完整性也面临着分层、脱粘等内部缺陷的严峻挑战。这类结构的蒙皮通常很薄，厚度在1mm量级，缺陷也大多分布于此深度。工程上，要求能够稳定检出直径为6~25mm的微小缺陷。

为了对这类缺陷的响应行为进行精确分析，我们需要一个有效的力学模型。幸运的是，上述缺陷的几何尺寸与材料属性，恰好满足固体力学中弹性薄板小挠度理论的适用条件。因此，我们可以将一个潜在的圆形缺陷简化为一个受法向均布载荷、周边被固支的圆形薄板模型（如图1所示）。在这个模型中，“周边固支”巧妙地模拟了缺陷边缘与完好材料的连接状态，而“均布载荷”则精确地复现了真空加载条件下，缺陷上下表面因压力差而承受的均匀力。

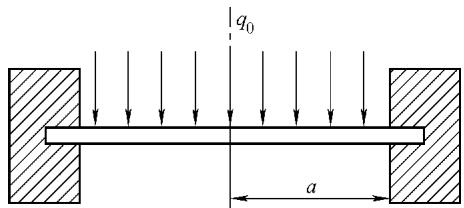
图1 缺陷的受力模型

该模型的一个重要优势在于其变形规律存在解析解。板中心层的挠度分布可由下式描述：

$$ w_{0} = /frac{q_{0}a^{4}}{64D}/left(1 - /frac{r^{2}}{a^{2}}/right)^{2} $$

式中各参数的物理意义如下：

• w₀: 距离圆心r处的离面位移（挠度）。
• q₀: 施加的均布载荷，在真空加载中即为内外压力差。
• a: 缺陷的半径。
• D: 材料的弯曲刚度，其表达式为 D = Et³ / [12(1 - μ²)]，其中E是材料的弹性模量，t是板的厚度，μ是泊松比。

这个公式构成了我们后续定量分析检测灵敏度的基石。

2. 错位量与测量灵敏度的内在关联

在错位散斑干涉技术中，检测灵敏度通常通过干涉条纹的疏密来体现，而一级条纹的出现便对应着一个特定的离面位移量。

从上述挠度公式可知，缺陷中心的挠度最大（此时 r = 0）：

$$ w_{/mathrm{max}} = /frac{q_0a^4}{64D} $$

为了使推导更具普适性，我们对公式进行无量纲化处理。定义无量纲挠度 w = w₀ / wₘₐₓ，无量纲半径 x = r / a，以及相对错位量 k = δx / a。经过简化，挠度方程变为一个优雅的形式：

$$ w = (1 - x^{2})^{2} $$

错位散斑技术的核心在于比较同一点在错位前后的位移。因此，我们将关注点聚焦于沿错位方向且穿过圆心的一条直线上，因为所有关键的干涉条纹信息都会在此呈现。设想一个错位后的图像，其位移可以表示为：

$$ w^{/prime} = [1 - (x - k)^{2}]^{2} $$

那么，这条直线上“对应点”的离面位移差 δw 便是：

$$ /delta w = w - w^{/prime} = k[4x^{3} - 6kx^{2} + 4(k^{2} - 1)x + 2k - k^{3}] $$

该位移差 δw 直接决定了干涉条纹的分布与级次。图2直观地展示了在不同相对错位量（δx / D，其中D为缺陷直径）下，δw 随位置 x 的变化情况。

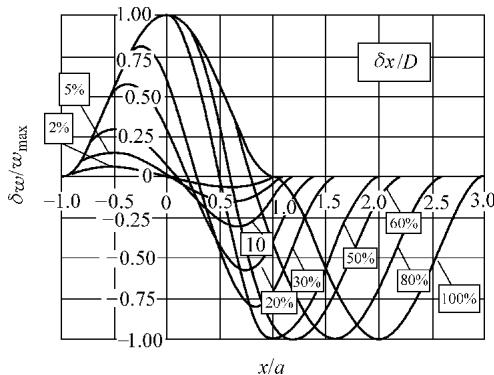
图2 缺陷中心位移差随错位量的变化

为了建立错位量与灵敏度的定量关系，我们需要找到 δw 的最大值，它对应着最高的条纹级次。通过求解极值，我们得到两个极值点的位置：

$$ x_{1,2} = /frac{k/pm/sqrt{/frac{4}{3} - /frac{1}{3}k^2}}{2} $$

将极值点代回计算出的 δw，便得到该错位量下的相对灵敏度。图3清晰地描绘了这一关系，其横轴为相对错位量 k_δx = δx / D，纵轴为相对灵敏度 k_sen = δw / w_max。

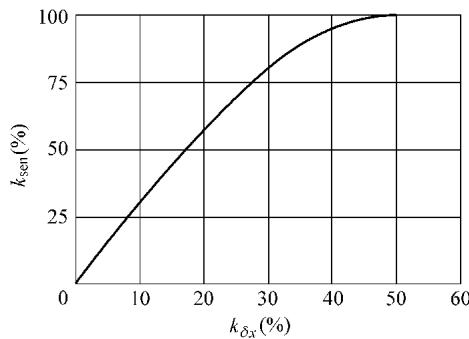
图3 错位量与测量灵敏度之间的关系

从这两张图中，我们可以提炼出两条关键规律：

1. 灵敏度的饱和效应：随着错位量的增加，检测灵敏度随之提高。但当相对错位量达到50%（即错位量为缺陷直径的一半）时，灵敏度达到极限值，继续增加错位量不再带来灵敏度的提升。
2. 响应区域的扩大：从图2可以看出，随着错位量增大，出现干涉条纹的区域也相应扩大，其增大的长度恰好等于错位量。这一理论结果与大量实验现象及计算机模拟高度吻合。

当相对错位量低于20%时，错位量与灵敏度呈现出良好的线性关系，这正是位移梯度法解释条纹的基础。一旦超过这个范围，灵敏度的增长便会放缓，线性关系不再成立。

3. 无损检测中错位量的选择原则

基于上述分析，我们可以在实际的无损检测应用中，制定出选择错位量的核心原则。

核心原则：为获得最高检测灵敏度，应将错位量设置为所要检测的最小缺陷尺寸的一半。

一旦按此原则设定了错位量，对于尺寸等于或大于最小目标的缺陷，系统都能以最高灵敏度进行探测。此时，即便继续增加错位量，所关心的最小缺陷区域的条纹级次也不会再增加，但更大尺寸缺陷的条纹级次仍会随之增加。

在传统的照相或电子错位散斑技术中，我们通过数条纹级次来估算位移量。通常，可将出现一级干涉条纹所对应的离面位移视为该方法的测量灵敏度。例如，当圆形缺陷中心的离面位移达到所用激光波长的一半时，就会出现一级干涉条纹。

• 对于常见的氦氖（He-Ne）激光器（波长632.8nm），一级条纹对应的位移约为316.4nm。
• 对于半导体泵浦固体激光器（波长532nm），一级条纹对应的位移约为266nm。

因此，这类技术的位移检测灵敏度处于亚微米级别。但考虑到实际工况中存在的整体变形和噪声干扰，通常认为其稳定可检的最小位移在微米量级。要从复杂的信号中准确提取微米级的位移信息，对操作经验和数据解读能力提出了很高要求。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测复合材料无损检测，可靠准确。欢迎沟通交流，电话19939716636

技术的进步不止于此。每级干涉条纹的出现，代表着相位差 Δ 变化了 2π。传统的条纹计数法本质上是一种离散的、宏观的测量。而现代相移技术的引入，则彻底改变了游戏规则。它不再依赖数条纹，而是通过采集多幅相移图像，直接在像素级计算出实际的相位差。这一变革将相位测量的灵敏度提升了2到3个数量级，使位移检测精度轻松迈入纳米量级，为发现更早期、更微小的损伤提供了可能。