错位散斑干涉法（Shearography）的光学原理深度解析

错位散斑干涉法，通常称为剪切散斑干涉（Shearography），是一种精密的共光路、自参考干涉测量技术。其独特之处在于，它并非直接测量物体的绝对位移，而是测量位移的梯度，这使其在振动、应变及无损检测（NDT）领域中对环境扰动具有优异的免疫力。

其基本工作流程是：激光通过一个特制的光学错位装置后，在CCD（或早期的感光底片）光敏面上形成被测物体的两个相互错开微小距离的图像。这两个图像本质上是来自同一物体的两束相干光，它们相互干涉，形成一张携带着物体表面形貌信息的散斑图。当物体在外力作用下发生变形时，这张散斑图也会随之发生可预测的变化，通过分析这种变化，即可反演出物体的变形信息。

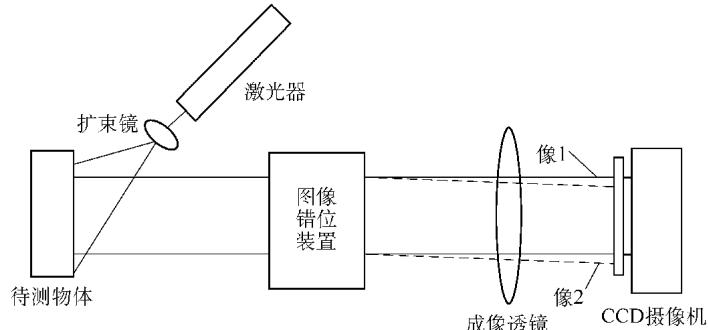
图1 激光错位散斑干涉法光路示意图

核心机制：“对点”成像与错位量

实现这一功能的关键是图像错位装置，其具体形式多样，可以是光楔、沃拉斯顿棱镜（Wollaston Prism）或特殊配置的迈克尔逊干涉光路等。该装置的核心功能是将从物体表面反射的一束光，按预设角度巧妙地分成两束。

这种分束效应导致了一个独特的成像关系：物体上的任意一点，都会在成像面上形成两个独立的像点。反之，成像面上的任何一个像点，实际上都同时接收了来自物体表面两个不同点反射的光波。我们将成像面上这两个相关的点称为“对点”，它们总是成对出现，如图2所示。这对“对点”在像平面上的空间距离，被定义为错位量或剪切量，通常设为 δx。

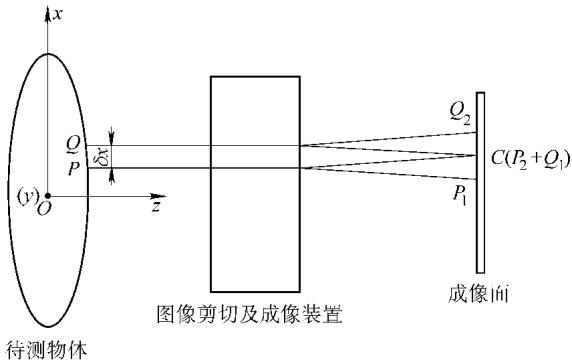
图2 “对点”的成像关系

数学描述：从光波到干涉强度

为了从物理上理解变形如何被编码到干涉条纹中，我们需要借助数学工具来描述光波的行为。

假设物体表面 P(x,y) 点反射的光在像面上形成的波前可以表示为：

F(x,y) = Ae^iφ(x,y)

其中，φ(x,y) 是一个与表面微观形貌相关的随机相位，正是这个随机相位导致了散斑现象。A 是光波振幅，为简化分析，我们假设在整个视场内 A 为常数，因为它对干涉条纹的形成不起决定性作用。

同理，与P点构成“对点”关系的 Q(x + δx, y) 点，其在像面上形成的波前为：

F(x + δx, y) = Ae^{iφ(x+δx, y)}

在物体变形前，这两个波前在像面上叠加干涉，其光强 I 为：

I = |F(x,y) + F(x + δx, y)|² = 2A²(1 + cosβ)

这里的 β = φ(x + δx, y) - φ(x,y) 是两个“对点”光波到达像面时的相位差。由于 φ 是随机的，β 也是一个在空间上无规则变化的随机变量，这构成了初始的散斑场。

当物体变形后，P点和Q点分别移动到新的位置 P’ 和 Q’，位移量为 (u,v,w)。这导致光程发生变化，相应地，光波的相位也发生改变。P点和Q点原来的相位 φ(x,y) 和 φ(x + δx, y) 分别增加了由变形引起的附加相位 δ(x,y) 和 δ(x + δx, y)。此时，变形后的波前变为：

F’(x,y) = Ae^{i[φ(x,y) + δ(x,y)]} F’(x + δx,y) = Ae^{i[φ(x+δx,y) + δ(x+δx,y)]}

变形后像面上的光强 I’ 为：

I’ = 2A²[1 + cos(β + Δ)]

其中，Δ = δ(x + δx, y) - δ(x,y) 是核心物理量。它代表了因变形而产生的、“对点”之间的相对相位变化，其中蕴含了我们关心的两点间相对位移信息。

干涉条纹的形成：两种技术路径

如何从前后两次的光强分布中提取出包含变形信息的 Δ 呢？历史上和现代技术中主要有两种方法。

1. 传统照相法：双重曝光与光学滤波

在数字相机普及之前，研究人员使用感光底片进行两次曝光。底片线性记录下的总光强为两次曝光之和：

I_T = I + I’ = 2A²[2 + cosβ + cos(β + Δ)]

如果直接观察这张底片，由于β项的快速随机变化，在人眼或普通显微镜的分辨能力内，光强会被平均掉，得到一个常数 4A²，因此看不到任何条纹。

要让条纹显现，需要进行一步光学傅里叶变换处理。利用三角函数和差化积公式，上式可改写为：

I_T = 4A²[1 + cos(β + Δ/2) · cos(Δ/2)]

在这个表达式中，cos(β + Δ/2) 是一个高频随机变化的载波项，而 cos(Δ/2) 是一个随变形缓慢变化的调制项。通过一个高通滤波系统（在频谱面中心设置一个挡板，滤除零频分量），可以抑制掉背景光和低频噪声。当 cos(Δ/2) = 0 时，I_T 在该点的空间频率为零，滤波后呈现为暗条纹。

暗条纹的条件是 Δ/2 = kπ, 其中 k = ±0.5, ±1.5, …。习惯上，我们用亮条纹进行级次计算，其条件为：

Δ = 2nπ (n为整数)

2. 电子散斑干涉法（ESPI）：数字相减

随着CCD/CMOS相机和计算机技术的发展，电子错位散斑干涉技术（有时也称TV Shearography）成为主流。其过程更为直接：分别采集变形前后的两幅数字散斑图，然后在计算机中进行像素对像素的相减运算。相减后图像的光强绝对值为：

I(x,y) = |I - I’| = |4A²sin(β + Δ/2)sin(Δ/2)|

这个结果非常直观：一个高频的散斑载波项 sin(β + Δ/2) 被一个低频的条纹项 sin(Δ/2) 所调制。当 sin(Δ/2) = 0 时，该点光强为零，形成暗条纹。因此，暗条纹的条件是：

Δ = 2nπ (n为整数)

对比两种方法可以发现，它们给出的条纹级次条件完全相同，这意味着两种技术测得的条纹图在本质上是一致的。一个有趣的区别是，在照相法中满足该条件的点是亮条纹，而在电子法中则是暗条纹，两者的黑白分布正好相反。

图3 典型的错位散斑干涉条纹图

图3展示了一张典型的错位散斑干涉图，它记录了一个周边固支的圆板在中心受均布载荷作用下的变形。这种对称的“蝶形”图案是错位散斑图的标志性特征，尤其在检测圆形缺陷时经常出现。它与激光全息或常规ESPI检测中常见的同心圆环条纹（等位移线）截然不同，因为蝶形图案反映的是位移的梯度，而非位移本身。

相位差Δ的确定：连接变形与条纹

要使测量定量化，必须建立相位差 Δ 与物体实际位移 (u, v, w) 之间的精确关系。这需要进行一番几何光程计算。

参考图4的光路几何关系，可以推导出由P点位移引起的光程变化 δl(x,y)。

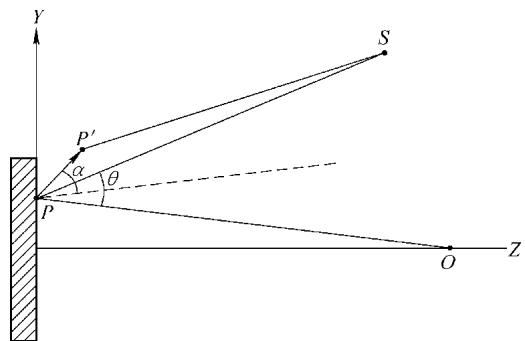
图4 位移与光程关系

经过一系列推导并略去高阶小量，可以得到 P 点和 Q 点各自的光程变化量 δl(x,y) 和 δl(x+δx, y)。而我们关心的相对相位差 Δ 正是这两个光程变化之差所对应的相位：

Δ = (2π/λ) [δl(x + δx, y) - δl(x, y)]

最终，可以得到错位散斑干涉测量技术的基本关系式：

Δ = (2π/λ) [Aδu + Bδv + Cδw]

其中，δu, δv, δw 分别是“对点”P和Q在x, y, z方向上的位移分量之差。系数 A, B, C 是与光源位置 (x_s, y_s, z_s) 和观察点位置 (x_o, y_o, z_o) 相关的几何因子。

这个公式构成了错位散斑干涉技术从干涉图像到定量变形分析的桥梁。与激光全息和常规ESPI技术直接给出近似等位移（通常是离面位移w）的条纹图相比，错位散斑干涉图的物理含义更为复杂，其条纹直接关联到位移的一阶偏导数。这种特性使得它对材料内部的局部缺陷（如脱粘、裂纹）所引起的应力集中异常敏感，但也对条纹的解读和数据处理提出了更高的要求。因此，要获得一张信噪比高、结果可靠的图谱，对样品制备、设备参数配置和后续算法处理都有极高要求。这正是专业检测实验室的核心价值所在。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测结构变形与应力分析，可靠准确。欢迎沟通交流，电话19939716636