1962年，贝尔实验室的Rigden和Gordon在研究激光时，首次观察到一种奇特的现象：当高相干性的激光照射到粗糙物体表面时，其成像面上会布满无规则的明暗斑点。这种被称为“激光散斑”的现象，在当时被视为一种影响图像分辨率的噪声，是早期激光全息技术中亟待消除的干扰。
然而，到了20世纪70年代，Leendertz和Butters等人提出了一个颠覆性的问题：既然散斑无法轻易消除，我们能否反其道而行，利用它来进行精密测量？这个设想开启了光学测量的一个全新领域。
1970年，Leendertz正式开创了散斑干涉计量学，这是一种利用散斑干涉来检测光学粗糙表面的新方法。其原理在本质上与全息干涉计量一脉相承，但在实现形式上却灵活得多，不仅支持传统的光学方法，更能与现代电子学和数字技术无缝结合。
传统的散斑干涉（Speckle Pattern Interferometry, SPI）依赖光学胶片记录散斑场，再通过光学信息处理技术提取变形信息。而其电子化和数字化的版本——电子散斑干涉（Electronic Speckle Pattern Interferometry, ESPI）或数字散斑干涉（Digital Speckle Pattern Interferometry, DSPI），则使用CCD等光电器件直接记录，并通过电子与数字信号处理技术来分析数据。目前，ESPI这一缩写已成为行业内的通用术语。
几乎与散斑干涉技术诞生同步，研究人员便开始探索用电视系统和计算机技术取代传统的光学胶片处理和光学滤波。随着计算机算力的飞速发展，ESPI凭借其操作简便、速度快、自动化程度高等优势，迅速成为全息散斑计量领域中最具工业实用价值的技术之一。在ESPI中，原始的散斑干涉场被光电器件转换为电信号，信息提取过程由电子技术完成，结果可实时显示在监视器上或存入计算机进行深度分析。
ESPI与传统光学方法的一个根本区别在于获取变形信息的原理。传统的光学二次曝光是一种“相加”技术，而ESPI的核心则是“图像灰度值相减”技术，这为其实现实时动态测试奠定了基础。
在散斑测量领域，主要有两大技术分支：
从技术迭代的角度看，依赖全息干版照相、化学冲洗和光学再现的传统方法可视为第一代技术，其流程繁琐耗时，严重制约了工业应用。而以电子图像处理取代化学处理的ESPI和电子错位散斑干涉（ESSPI），则标志着第二代“电子图像时代”的到来。通过CCD相机记录变形前后的散斑图，并以电子化方式进行图像比对与处理，实现了干涉条纹图的实时显示，从而能够对变形过程进行动态监测。
当物体表面被激光照射时，由于激光的高度相干性，从表面各微观散射点反射的光波会发生相互干涉，在空间中形成一个随机分布的、由明暗光斑组成的“空间散斑场”。ESPI技术的核心，就是将这个携带物体表面信息的散斑场与一束参考光进行叠加干涉，然后用CCD相机捕捉这个干涉场，形成一幅二维散斑图。
整个工作流程可以分解为以下步骤，如图1所示：
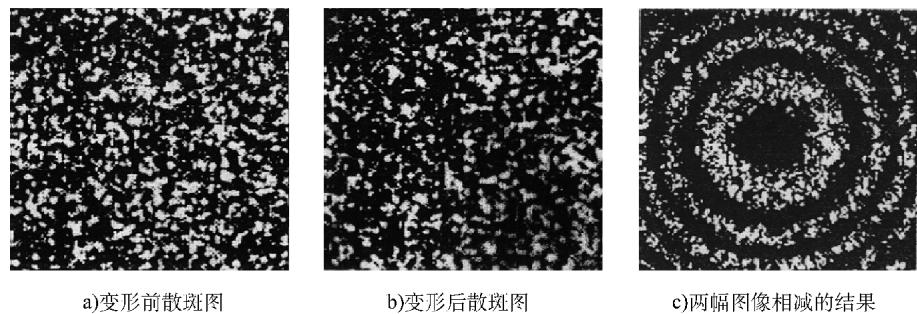图1 电子散斑干涉条纹图的形成过程
从物理学角度看，变形前散斑图上任意点(x, y)的光强 I(x,y) 可表示为：
I(x,y) = a(x,y) + b(x,y)cos(φ(x,y))
其中，a 是背景光强，b 是散斑调制度，φ 是物光波与参考光波间的随机相位差。
由于ESPI通常用于检测微小变形，可以假定变形前后背景光强 a 和调制度 b 保持不变，仅有相位 φ 发生变化。变形后光强为 I'(x,y)，两幅图像相减后的光强 I_sub 为：
I_sub = |I'(x,y) - I(x,y)| = b(x,y)|cos[φ(x,y) + Δ(x,y)] - cos[φ(x,y)]|
= 2b(x,y)|sin[φ(x,y) + Δ(x,y)/2]sin[Δ(x,y)/2]|
在这个表达式中，Δ(x,y) 是由表面位移引起的相位变化，是我们需要测量的核心物理量。sin[φ(x,y) + Δ(x,y)/2] 是一个高频随机项，构成了图像的散斑背景。而 sin[Δ(x,y)/2] 是一个随位移连续变化的低频项，它调制了整个图像的亮度。当 Δ(x,y) = 2Nπ (其中 N = 0, ±1, ±2, …) 时，sin[Δ(x,y)/2] 为零，图像上出现暗条纹。这里的N就是干涉条纹的级次。
相位变化 Δ(x,y) 与表面位移矢量 d(x,y) 之间的关系可以表示为：
Δ(x,y) = S(x,y) · d(x,y) = S(x,y) · [iu(x,y) + jv(x,y) + kw(x,y)]
其中 S(x,y) 被称为灵敏度矢量，其方向和大小由检测光路的具体布置决定。这个公式建立了可观测的干涉条纹级次与待测的表面位移之间的定量桥梁。
根据待测位移分量的不同，ESPI主要有两种常见的光路配置：离面位移测量光路和面内位移测量光路。
在无损检测应用中，测量垂直于物体表面的离面位移（Out-of-Plane Displacement）最为常见。这种配置有时也被称为电视全息（TV-holography）。其典型光路如图2所示。
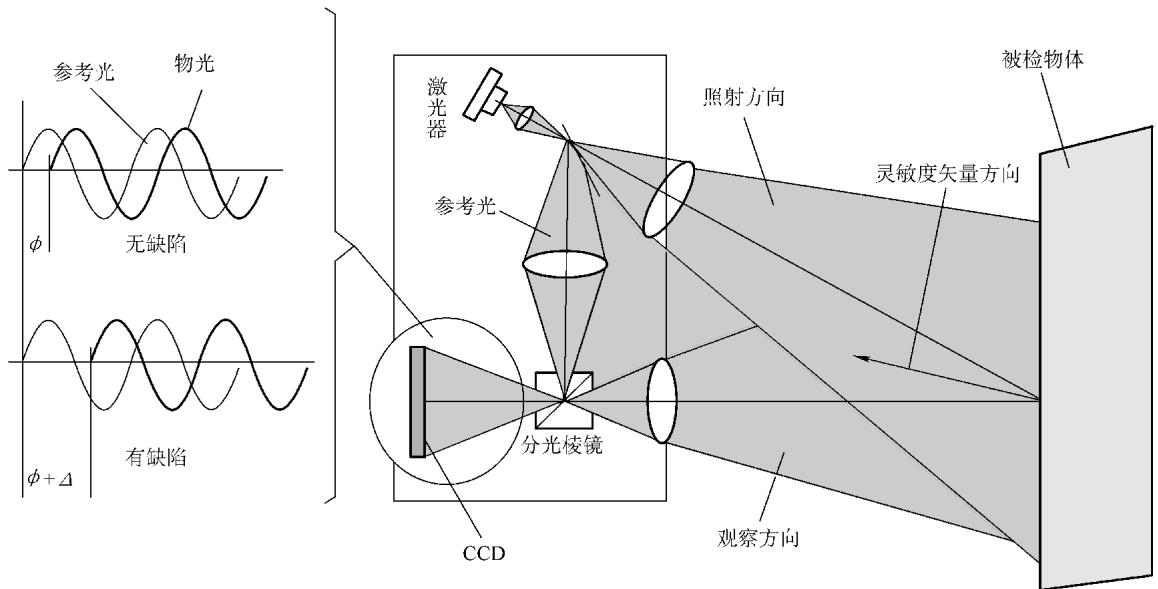图2 电子散斑干涉测量离面位移的光路示意图
在该光路中，灵敏度矢量的方向是激光照明方向与相机观察方向的角平分线方向。因此，干涉条纹反映的是表面位移在灵敏度矢量方向上的投影。位移分量 d 与条纹级次 N 的关系为：
d = Nλ / [2cos(α/2)]
式中，λ 是激光波长，α 是照明方向与观察方向的夹角。
在实际工程应用中，光学测头与被测物体的距离通常远大于激光器与摄像机之间的距离，这使得灵敏度矢量的方向与物体表面法线（即离面方向）的夹角非常小。因此，可以近似认为该光路只对离面位移 w 敏感，公式可简化为：
w = Nλ / 2
这个简化的公式非常直观：在该光路下，每出现一级新的干涉条纹，就代表物体表面在该点的离面位移增加了约半个激光波长。
图3展示了用于测量面内位移（In-Plane Displacement）的光路配置。其关键特征是，一束激光经分光后，形成两束光以对称的角度 α 照射在物体表面。
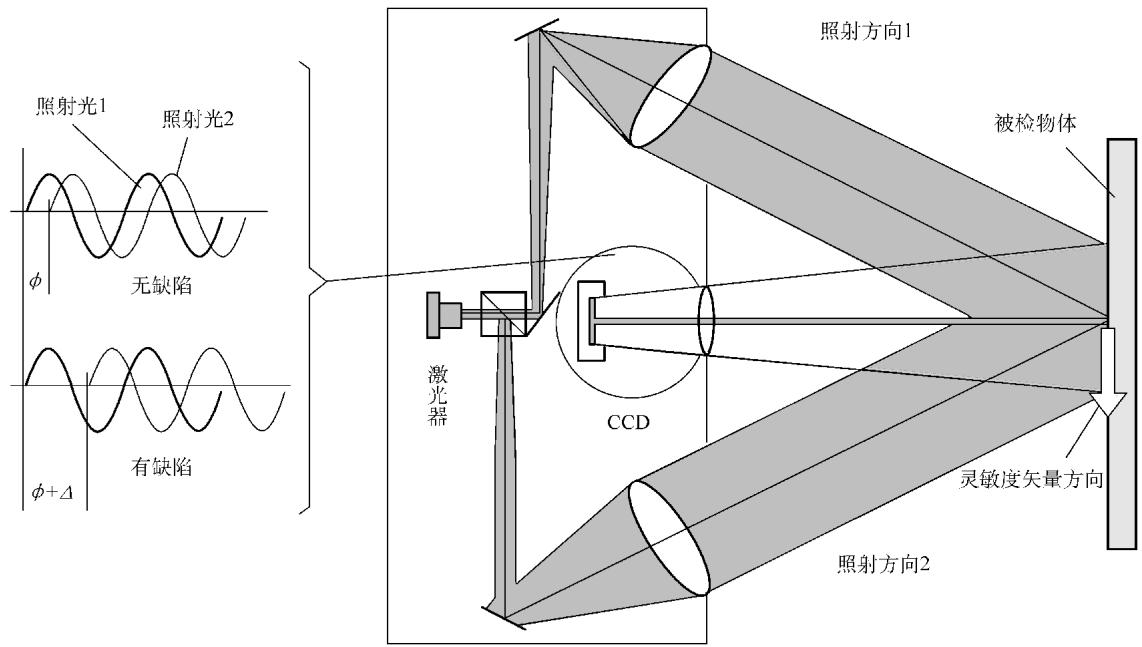图3 电子散斑干涉测量面内位移的光路示意图
在这种配置下，灵敏度矢量位于两束入射光构成的平面内，且方向平行于被测物体表面。因此，它只对与灵敏度矢量方向平行的面内位移分量敏感。面内位移 d 与条纹级次 N 的关系为：
d = Nλ / [2sin(α/2)]
从公式可以看出，面内位移测量的灵敏度与两束照明光之间的夹角 α 直接相关，夹角越大，灵敏度越高。
ESPI不仅能胜任静态或准静态的位移测试，其真正的威力更在于对动态过程的捕捉能力，如谐振动及瞬态变形测量。在振动分析领域，ESPI及其衍生技术（如ESSPI）凭借其在实时性、图像质量上的优势，已在很大程度上取代了传统的激光全息干涉测量。
当被测物体在正弦波激励下发生稳态振动，并在其固有频率处产生共振时，时间平均法ESPI是理想的检测工具。这种方法的ESPI光路和静态测量相同，但由于振动频率远高于CCD相机的帧率，相机采集到的是一个振动周期内光强的积分平均效果。
I_avg(x,y) = a(x,y) + b(x,y)cos(φ(x,y))J_0(4πu_0(x,y)/λ)
将振动状态的平均图像与振动前的静态图像相减，可以实时观察到由零阶贝塞尔函数 J_0 描述的干涉条纹。这些条纹的分布清晰地勾勒出物体在共振状态下的振型，而条纹的节点（最亮处）则对应振幅为零的区域。通过扫频激励，可以快速识别出结构的各阶固有频率及其对应的振动模态。
对于稳态谐振动，如果需要定量测量其振幅和相位，则可采用频闪照明技术。通过声光调制器（AOM）对连续激光进行调制，使其在振动周期的特定相位点发出短促的光脉冲。通过同步控制，CCD相机在每个周期内采集到的都是物体在同一位置的“冻结”图像。通过采集并相减两个不同相位点的“冻结”散斑图，即可获得反映这两个状态间位移的干涉条纹，从而精确计算出振幅和相位信息。
当面对非谐振动，甚至是冲击、爆炸等瞬态变形时，上述两种方法便无能为力。此时，双脉冲技术应运而生。该技术采用脉冲激光器（如红宝石激光器）在极短的时间间隔内（通常为2μs至800μs）发射两次脉冲，同步记录下两幅“冻结”了物体在两个瞬间状态的散斑图。通过比较这两幅散斑图，可以精确获得这两个瞬间之间的表面位移场，从而实现对高速瞬态过程的定量分析。
这些动态与瞬态检测技术的实现，对激光器选型、光路同步控制、数据采集与处理算法均提出了极高的要求。这正是专业检测实验室的核心价值所在。 精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测动态振动分析、材料微应变测量，可靠准确。欢迎沟通交流，电话19939716636
为了将理论与实践相结合，我们以丹麦Dantec Dynamics公司生产的Q-300三维ESPI系统为例，展示现代商用检测系统的能力。
图4 用于三维位移及振动分析的电子散斑检测系统（Dantec Q-300）
该系统是一套功能高度集成的电子散斑干涉平台。其设计巧妙之处在于，利用两组对称入射角度和四个独立的照明方向，通过软件选择性地开启不同光路，即可在同一套硬件上实现离面位移和面内位移的测量，甚至可以进行完整的三维位移场分析。
系统主要技术参数：
可选硬件与软件模块：
该系统充分体现了现代ESPI技术向着集成化、自动化和多功能化的发展方向，为科研和工业领域的材料表征、结构健康监测和产品质量控制提供了强大的工具。
首页
检测领域
服务项目
咨询报价
