激光全息干涉检测技术：原理、方法与应用解析

激光全息干涉测量，作为一种高精度的非接触式测量技术，其核心在于利用光的干涉原理，将物体表面发生的微米乃至亚微米级别的形变或振动，转化为肉眼可见的干涉条纹图。其基本操作流程与全息照相一脉相承，区别仅在于曝光策略：根据测量需求，可选择对物体变形前后进行两次曝光（双曝光法）、仅在初始状态曝光一次（实时法），或在振动周期内连续曝光（时间平均法）。本文将对这三种主流方法的技术实现与应用特点进行深入剖析。

一、双曝光法：定格静态形变的“快照”

双曝光法通过在同一张全息干板上记录物体变形前后的两个状态，从而“冻结”并量化其间的静态位移。

如图1所示的光路中，激光束经分光后形成两路：一路作为参考光，另一路照射在被测物体上形成物光。空间滤波器（SF₁、SF₂）用于优化光束质量，确保干涉效果。操作时，首先在物体处于初始状态时开启快门，进行第一次曝光；随后对物体施加载荷使其产生微小形变，再进行第二次曝光。

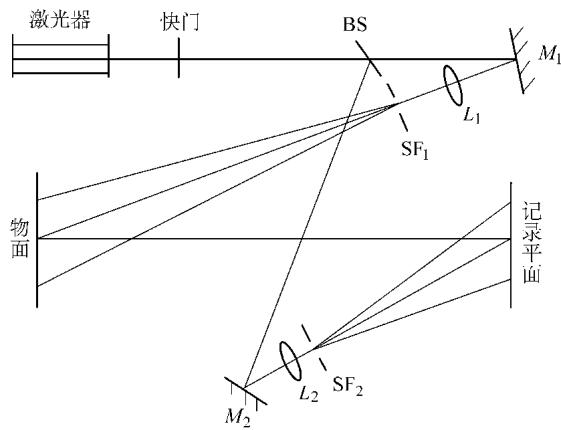图1 双曝光法记录光路

经过显影、定影处理后，当用原始的参考光束照射这张“双重”全息图时，变形前后的两个物光波前会被同时再现。由于形变引入了光程差，这两个波前将发生干涉，形成稳定的干涉条纹图，这些条纹精确地描绘了物体表面的位移分布。

1.1 干涉条纹的数学诠释

要理解这些条纹的物理意义，我们需要深入其背后的数学原理。设物体变形前后的物光波复振幅分别为：

• 变形前: O = O₀(x,y) exp[iφ₀(x,y)]
• 变形后: O’ = O₀(x,y) exp[iφ(x,y)]

参考光的复振幅为 R = R₀(x,y) exp[iφ_r(x,y)]。

两次曝光记录的总光强 I 是两次曝光光强 I₁ 和 I₂ 的叠加： I = I₁ + I₂ = (O* + R*)(O + R) + (O’* + R*)(O’ + R)

当用原参考光 R 照明处理后的全息图时，透射光波 ψ 中我们最感兴趣的是再现的原始像光波 U₂。其光强 I_像 可以表示为：

I_像 = U₂* · U₂ = 2R₀⁴ O₀² [1 + cos(φ - φ₀)] = 4R₀⁴ O₀²cos²((φ - φ₀)/2)

这个公式揭示了核心机制：再现像的光强分布直接由变形前后物光波的相位差 (φ - φ₀) 决定。

• 当相位差 (φ - φ₀) = 2mπ (m = 0, ±1, ±2, …)，光强最大，形成亮条纹。m=0 对应位移为零的区域，即零级条纹。
• 当相位差 (φ - φ₀) = (2m - 1)π (m = 1, 2, 3, …)，光强为零，形成暗条纹。

1.2 从相位差到物理位移

那么，相位差如何与实际的物理位移 d 建立联系？如图2所示，假设物体表面P点因变形移动到P’点，位移量为 d。从光源S到P点再反射到全息干板H的光程，与从S到P’再到H的光程存在差异。

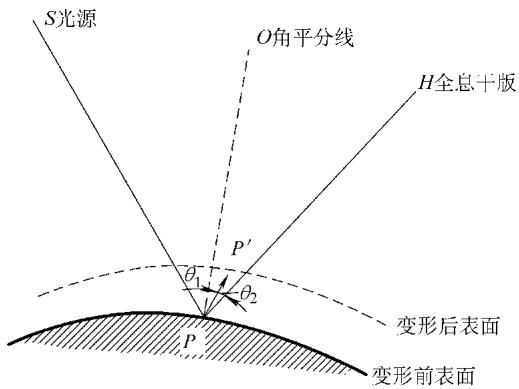图2 物体变形前后的位移与相位差关系

由于位移 d 极小，我们可以认为入射光、反射光与位移方向的夹角 θ₁ 和 θ₂ 基本不变。由此引起的光程差 Δ 为：

Δ = d cosθ₁ + d cosθ₂

相应的相位差 (φ - φ₀) 则为：

φ - φ₀ = (2π/λ)Δ = (2πd/λ)(cosθ₁ + cosθ₂)

为了方便分析，我们引入两个角度：θ = (θ₁ + θ₂)/2（入射光与反射光夹角的半角）和 ψ = (θ₁ - θ₂)/2（灵敏度矢量方向与位移方向的夹角）。公式可简化为：

φ - φ₀ = (4πd/λ)cosψcosθ

结合亮条纹条件 φ - φ₀ = 2mπ，我们最终得到位移测量的核心公式：

dcosψ = mλ / (2cosθ)

其中，λ 是所用激光的波长。该式表明，条纹级数 m 直接对应于位移矢量 d 在灵敏度矢量方向（入射光与反射光夹角的角平分线方向）上的投影分量。在许多实际光路中，照明与观察方向接近于表面法线，此时可以近似认为干涉条纹图就是物体离面位移的等值线图。

在无损检测领域，这种方法尤为有效。如图3所示，一块周边固定的方板在中心受力后，其双曝光全息干涉图呈现出一系列环状条纹。条纹从位移为零的边缘（0级）向中心递增，中心的位移最大。这种多级环状条纹包围的区域，在复合材料检测中常常是分层、脱粘等内部缺陷的典型特征。

图3 固支方板受中心集中载荷的双曝光法条纹图

二、实时法：捕捉动态变化的“直播”

实时法的光路布置与双曝光法一致，但操作流程赋予了它实时观测的能力。实验时，首先只记录物体初始状态的全息图。底片经显影、定影后，被精确地放回原位。此时，用参考光照射全息图，再现的物光波将与正被实时加载、持续变形的物体所反射的真实物光波发生干涉。

观察者因此可以看到随载荷变化而实时演变的动态干涉条纹。

优点：

• 动态观测：能够实时观察条纹的生消、移动和疏密变化，直观地了解变形过程。
• 参数优化：便于确定零级条纹位置、判断位移增加方向，为双曝光法精确加载提供实验参数指导。

缺点：

• 复位精度要求高：全息底片处理后必须精确复位到曝光时的位置，任何微小偏差都会引入额外条纹，干扰测量。为此，常需要采用原位处理装置或数字全息技术来规避此问题。
• 条纹对比度较低：由于再现像与实时物光的光强差异等因素，实时法干涉条纹的对比度和清晰度通常不如双曝光法。

双曝光法以其操作简便、条纹清晰、适于精确定量分析而著称，但它无法预估变形量，可能需要多次尝试。实时法恰好弥补了这一点，成为实验探索阶段的有力工具。要获得一张信噪比高、结果可靠的图谱，对样品制备、光路调校、环境稳定性都有极高要求。这正是专业检测实验室的核心价值所在。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测材料微观变形与振动分析，可靠准确。欢迎沟通交流，电话19939716636

三、时间平均法：解析周期振动的“积分”

当被测对象进行稳态周期性振动时，时间平均法便派上用场。其光路与前两种方法相同，但曝光方式独特：曝光时间远大于物体的振动周期，相当于在一次曝光中连续记录了物体在振动轨迹上无数个位置的状态。

本质上，时间平均法可视为多次曝光干涉的一种极限情况。经过积分效应，再现的全息图上会形成携带物体振幅信息的干涉条纹。其再现像光强 I(x,y) 可由零阶贝塞尔函数 J₀ 的平方来描述（此处略去推导）：

I(x,y) = K(x,y) J₀²[(2π/λ)A(x,y)(cosθ₁ + cosθ₂)]

其中：

• K(x,y) 是与位置相关的常数。
• A(x,y) 是该点处的振动幅值。
• θ₁, θ₂ 定义同前。

如图4所示的零阶贝塞尔函数平方曲线上，当函数值为零时，对应暗条纹。

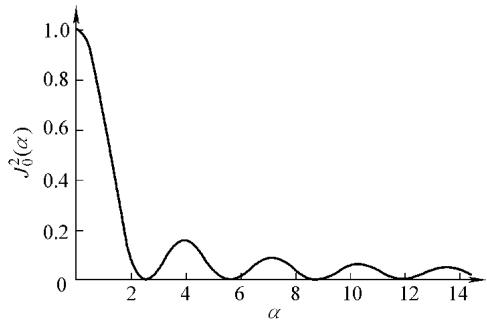图4 零阶贝塞尔函数平方的曲线

令 α = (2π/λ)A(x,y)(cosθ₁ + cosθ₂)，当 J₀(α) = 0 时出现暗条纹。设 J₀(α) = 0 的根为 α_i (i = 1, 2, 3, …)，则振幅可由下式计算：

A(x,y) = (λ/2π) * [α_i / (cosθ₁ + cosθ₂)]

与双曝光法类似，条纹级次 i 反映了振幅在灵敏度矢量方向上的投影。一个关键区别在于，时间平均法的条纹级次（即贝塞尔函数的根）并非等间距整数。例如，前四级暗条纹对应的 α 值约为 2.40, 5.52, 8.65 和 11.79。

从图中还可以看出，振幅为零处（即振动中的节线位置）对应最亮的零级条纹。随着条纹级次的增加，亮条纹的光强迅速衰减，例如，第1、2、3级亮条纹的光强分别仅为零级条纹的16%、8.9%和2.3%。这意味着高级次条纹的对比度会显著下降，观测和分析难度随之增加。