漏磁检测技术精解：缺陷尺寸的量化方法与模型

日期：2025-07-28 浏览：5

漏磁检测技术精解：缺陷尺寸的量化方法与模型

漏磁场（MFL）检测技术的一大核心优势，在于其能够对检测到的缺陷信号进行量化评估。在实际应用中，影响漏磁信号的缺陷几何参数纷繁复杂，涵盖了深度、宽度、倾斜角、形状乃至其在材料内部的埋藏深度等。然而，对于关乎结构安全性的表面缺陷而言，其深度与宽度无疑是两个最关键的评价指标。因此，整个量化过程可以被精炼为对这两个核心维度的精确反演。

一、裂纹宽度的量化：一个被低估的关键参数

在漏磁检测发展的早期，研究人员的目光大多聚焦于缺陷深度的量化，而宽度的影响及其量化方法在很长一段时间内未得到充分重视。直到20世纪70年代末，Lord和Hwang等先驱通过对矩形槽的初步研究，才推测漏磁场法向分量（B_y）的两个信号峰值之间的横向距离与裂纹宽度可能存在线性关联。

近期的研究则更为明确地证实，B_y分量中确实蕴含着丰富的裂纹宽度信息。这一发现意义重大，它意味着我们可以在不显著增加检测系统复杂度的前提下，实现对宽度和深度的同步量化。

我们定义一个关键参数——横向峰-峰间距 S_y(p-p)，即漏磁场B_y分量信号曲线上最大值与最小值之间的横向距离，如下图所示。

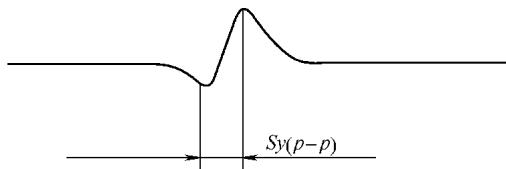图1 漏磁场B_y分量与横向距离S_y(p-p)的定义

通过大量的物理实验与数值模拟分析，一个清晰的规律浮出水面：S_y(p-p)不仅与缺陷宽度（w）相关，还受到传感器提离值（L，即传感器探头与工件表面的距离）的显著影响。三者之间存在一个确定的函数关系：

S_y(p-p) = f(L, w)

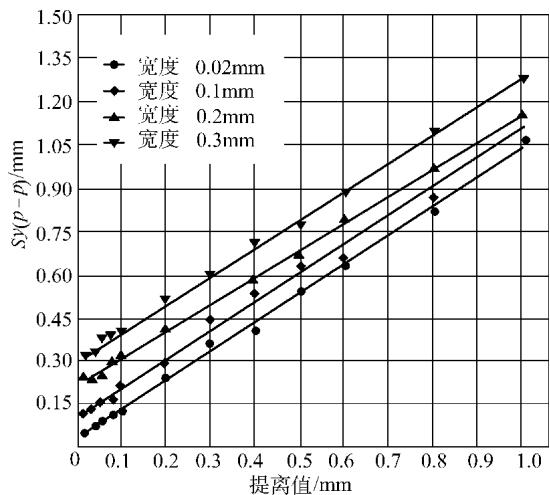图2 S_y(p-p)与矩形槽宽度及提离值的关系

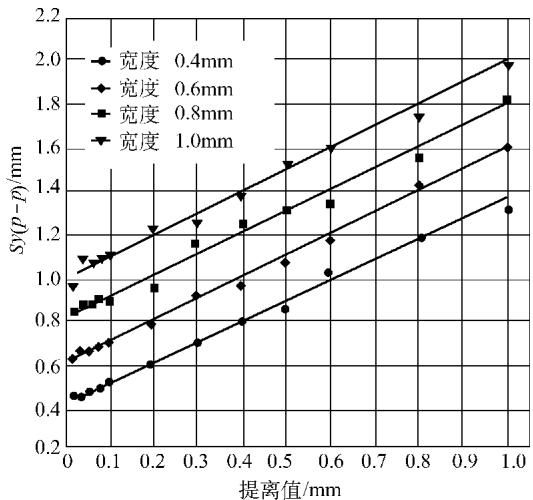图3 S_y(p-p)与矩形槽宽度及提离值的关系（续）

上图展示了在特定磁场强度（9000 A/m）下，对深度为0.2mm、宽度与提离值在0.02mm至1.00mm范围内变化的矩形槽进行数值计算得到的数据。从图中可以清晰地看到，S_y(p-p)值与矩形槽宽度呈现出良好的线性关系。

对这些数据进行拟合，可以得到如下的经验公式：

S_y(p-p) = 1.008w + 0.995L + 0.009

这个结果非常接近一个更为简洁、物理意义也更直观的形式：

S_y(p-p) ≈ L + w

采用这个简化公式，不仅极大地方便了工程应用，而且带来的系数误差仅为0.8%和0.5%，常数项0.009相对于提离值而言亦可忽略不计。这一结论在自然缺陷的检测中也得到了验证。

这个简洁的公式背后蕴含着双重应用价值。其一，在已知提离值的情况下，可以直接量化裂纹宽度。其二，它提供了一种巧妙的方法来反向标定传感器的实际提离值。在现场检测中，传感器通常被封装以作保护，直接测量其与工件表面的精确距离相当困难。利用该公式，我们只需在一个已知宽度为 w 的人工缺陷上进行扫查，通过测量信号两个极值点之间的时间差 t，即可计算出S_y(p-p)：

S_y(p-p) = v × t

其中，v 为传感器的扫查速度。随后，便可轻松推算出传感器的提离值 L：

L = (v × t) - w

二、裂纹深度的量化：挑战与修正模型

对于表面裂纹，深度是决定材料或构件力学性能退化的首要因素。因此，如何从复杂的漏磁信号中精确提取深度信息，始终是MFL检测技术研究的核心课题。业界已达成广泛共识：在一定条件下，对于宽度相同的裂纹，其漏磁信号的峰-峰值与裂纹深度呈线性关系。这构成了漏磁检测定量化的理论基石。

然而，理论与现实之间存在一道鸿沟。在实际工件中，我们面临两大难题：

宽度不一：自然缺陷的宽度千差万别。
形状各异：真实裂纹的几何形状远非规整的矩形槽可比。

要实现真正意义上的精确量化，就必须正面解决这两个问题。

宽度的非线性影响与修正模型

在深度量化的过程中，我们必须设法消除宽度变化带来的干扰。一个直观的思路是将不同宽度的裂纹信号“修正”或“归一化”到某个标准宽度上，再利用线性关系进行量化。

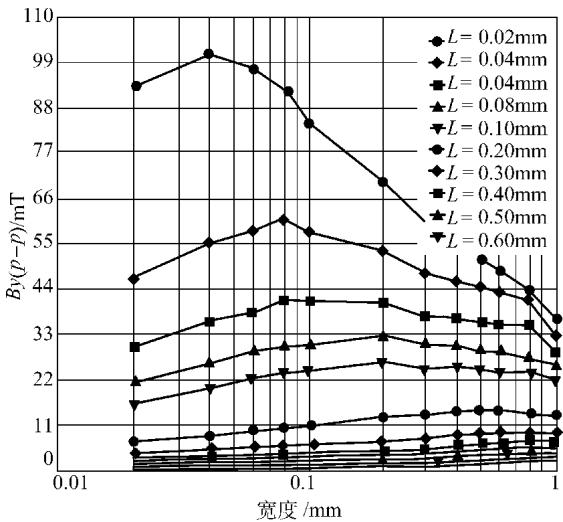图4 不同提离值(L)下，矩形槽宽度变化对S_y(p-p)值的影响曲线

上图揭示了一个反直觉但至关重要的现象：当缺陷深度固定时，随着宽度增加，信号峰-峰值并非单调变化，而是呈现出先增大后减小的趋势。更有趣的是，这个规律的“拐点”位置与提离值 L 密切相关。经过严谨计算发现，当缺陷宽度 w 恰好等于提离值 L 的两倍（即 w = 2L）时，检测到的信号峰-峰值达到最大。这一规律在改变磁化强度、缺陷深度乃至工件材质（如铸铁）时都表现出良好的一致性。

基于这一发现，我们可以构建一个宽度影响的修正模型：

基准定义：对于深度相同、提离值为 L 的检测场景，当缺陷宽度 w = 2L 时，检测到的峰-峰值最大，记为 B_y(p-p)_max。
修正因子 k：宽度的影响可以通过一个修正因子 k 来描述，它由缺陷宽度 w 和提离值 L 的比值决定。

B_y(p-p) = B_y(p-p)_max × k

当宽度 w ≤ 2L 时： k = (w / 2L)^α

当宽度 w > 2L 时： k = (2L / w)^β

其中，指数 α 和 β 的取值与提离值大小有关，可根据下表选取：

表1 α, β 的取值

提离值 / mm	α	β
<0.05	0.1	0.2
≥0.05 ~ 0.1	0.15	0.1
≥0.1 ~ 0.15	0.2	0.1
≥0.15 ~ 0.2	0.25	0.1
≥0.2 ~ 0.3	0.3	0.1
≥0.3 ~ 0.4	0.35	0.1
≥0.4 ~ 0.6	0.4	0.1
≥0.6 ~ 1.0	0.5	0.1

深度量化的四步流程

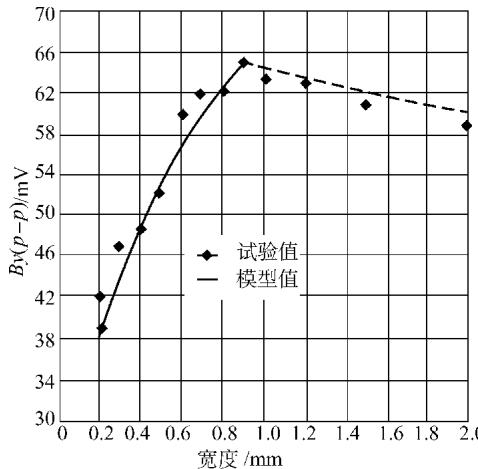图5 试验结果与模型计算结果比较

利用上述模型，我们可以对任意宽度和深度的矩形槽进行精确量化。本质上，这个模型的核心思想是建立一个以“宽度等于两倍提离值”为基准的“理想缺陷”，并将所有实际检测信号都归一化到这个基准上，从而消除宽度变量的干扰。具体操作流程如下：

建立初始线性关系：在固定的检测条件下（磁场、提离值），通过对一组已知宽度 w、不同深度 d 的人工缺陷进行检测，建立峰-峰值 B_y(p-p) 与深度 d 的初始线性关系： B_y(p-p) = c + b × d （其中 c 和 b 为待定系数）
修正线性关系至 w=2L 基准：将上述通过宽度为 w 的人工缺陷得到的线性关系，修正为宽度等于 2L 时的标准线性关系。
- 若 w ≤ 2L，修正后的关系为：B_y(p-p) = c + b × d × (w / 2L)^α
- 若 w > 2L，修正后的关系为：B_y(p-p) = c + b × d × (2L / w)^β （α 和 β 值按表1选取）
修正待测缺陷信号：将现场检测到的未知缺陷信号进行归一化。假设测得某缺陷宽度为 w₁，对应峰-峰值为 B_y(p-p)。
- 若 w₁ ≤ 2L，修正后的峰-峰值为：B_y(p-p)’ = B_y(p-p) / (w₁ / 2L)^α
- 若 w₁ > 2L，修正后的峰-峰值为：B_y(p-p)’ = B_y(p-p) / (2L / w₁)^β
计算最终深度：将修正后得到的峰-峰值 B_y(p-p)’ 代入步骤2中修正后的标准线性关系式中，即可反演出该缺陷的等效深度 d。