在无损检测领域，尤其是在处理微弱的缺陷信号时，背景噪声的干扰是一个无法回避的核心挑战。无论是来自设备本身的电磁干扰，还是由工件表面状态、振动等环境因素引入的噪声，都可能将珍贵的缺陷特征淹没，导致漏检或误判。图1展示了一种典型的周期性噪声信号在频域上的分布，其谱线清晰，能量集中。如何从混杂的信号中精确地提取出有效信息，是决定检测成败的关键。
图1 周期性噪声信号的典型频谱
随着数字化技术的发展，我们得以在计算机上对采集到的信号进行深度处理。其中一种针对周期性噪声的巧妙方法被称为“程序滤波”。
程序滤波的原理根植于对噪声特性的精准利用。如果我们将一个叠加在检测信号上的周期性噪声单独剥离出来，其在时间域内的某个频率分量可以被简化为一个标准的正弦函数：
$$ N(t) = A/sin /omega t $$
这里的核心思想是：如果我们以该噪声频率的整数倍进行同步采样，那么噪声信号在每个周期内的采样值将会呈现完美的重复性。
假设我们将采样频率设定为噪声基频的 m 倍（m 为整数），采集得到的数字序列为 N(i)，其中 i = 1, 2, ..., n，n 为序列总长度。在理想的采样条件下，由于采样的同步性，噪声信号将满足以下周期性关系：
N(i) = N(m + i) = N(2m + i) = ... = N(jm + i)
其中 j 为周期序数。
理解了这一点，消除该噪声的方法就变得异常直接。我们可以构建一个新的序列 N'(i)，其计算方式如下：
$$ N^{/prime}(i) = N(i + m) - N(i) = 0 $$
这个简单的差分运算，本质上是用一个周期后的噪声采样值去减掉当前时刻的噪声采样值。由于二者在理想情况下完全相等，其差值为零，从而实现了对该频率周期噪声的彻底消除。通过这种方式，原始信号 N(i) 中周期性噪声的影响被显著削弱。
在实际的检测系统中，这种方法的应用效果十分显著。图2与图3直观地展示了在漏磁检测中，对一个包含强周期噪声的缺陷信号应用“程序滤波”前后的波形变化。处理前，有效信号几乎被噪声淹没，信噪比（SNR）不足1；而经过程序滤波处理后，噪声背景变得平坦，缺陷信号清晰地凸显出来，信噪比提升至6以上。
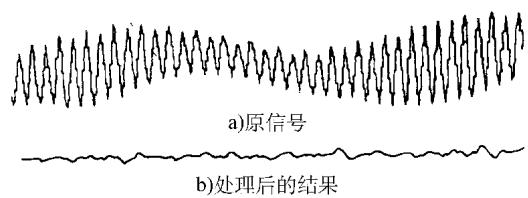图2 采用程序滤波后信号的处理结果
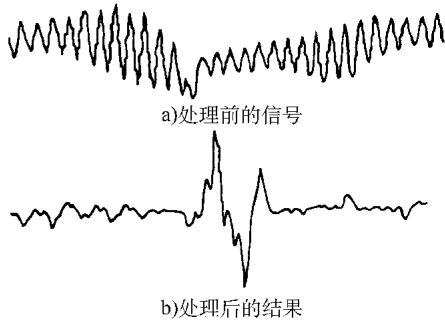图3 缺陷信号处理前后的波形对比
要实现这样理想的去噪效果，需要对噪声特性有精确的分析，并对信号采集和处理算法进行精细的调校。这正是专业检测实验室的核心价值所在，通过深厚的技术积累确保每一份数据的可靠性与准确性。
精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测无损检测，可靠准确。欢迎沟通交流，电话19939716636
程序滤波虽然高效，但其应用场景主要局限于稳定的周期性噪声。在真实的工业环境中，信号往往更为复杂，尤其是缺陷本身所产生的信号，通常是随机的、突发性的。对于这类非平稳信号，传统的谱分析或简单滤波方法就显得力不从心。
针对数字化的漏磁场检测信号，数字滤波、小波处理等更高级的方法提供了更广阔的解决思路。其中，小波分析（Wavelet Analysis）被认为是一种极具潜力的信号处理工具。
与傅里叶变换将信号分解为不同频率的正弦波不同，小波分析使用一组具有有限时长且形态可变的“小波”基函数来分析信号。这使得它能够同时提供信号在时域和频域的局部化信息，就像一个数学显微镜，可以聚焦到信号的任何一个细节上。这种“时频联合分析”的特性，使其在处理随机、突发信号时表现出无与伦比的优势，能够捕捉到常规谱分析方法容易忽略的瞬态特征，并给出更丰富的信息量。
图4展示了小波分析在钢丝绳检测中的一个应用实例。通过小波变换，可以将原始的、混杂的信号分解到不同的尺度（频率）上，从而有效地将代表局部损伤（如断丝）的突发信号与背景噪声分离开来，实现精准的缺陷识别与定位。
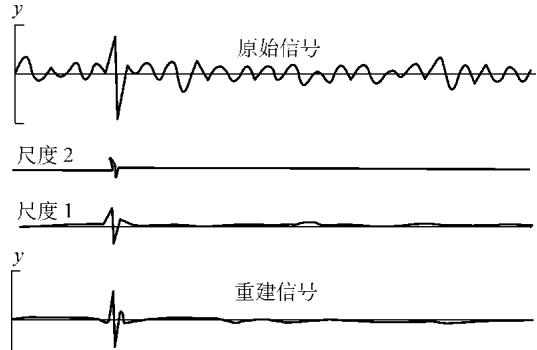图4 钢丝绳检测信号的小波分析结果
从巧妙利用周期性的程序滤波，到能够精细解析瞬态特征的小波分析，数字信号处理技术正不断推动无损检测向着更精确、更智能化的方向发展。选择合适的信号处理方法，是从海量数据中挖掘真实洞见的根本保障。
首页
检测领域
服务项目
咨询报价
