缺陷漏磁场特性解析：从理论模型到影响因素

漏磁检测（Magnetic Flux Leakage, MFL）的物理学基础相当直观：当一个铁磁性材料被外部磁场磁化后，如果其表面或近表面存在缺陷（如裂纹、凹坑），磁力线在缺陷处会发生畸变，一部分会“泄漏”到材料表面之外，形成所谓的“漏磁场”。通过高灵敏度的磁敏传感器捕捉并分析这个漏磁场，我们就能反推出缺陷的存在、位置乃至几何特征。因此，深入理解缺陷漏磁场的形成机理、分布规律及其影响因素，是整个漏磁检测技术体系的基石。

对漏磁场的研究路径主要分为两大类：试验测量与理论计算分析。前者提供物理世界的真实数据，后者则构建数学模型以求预测和解释。

试验测量：捕捉微观磁场的真实面貌

尽管利用磁敏元件探测漏磁场以发现缺陷的想法由来已久，但要精确地描绘出漏磁场的空间分布形态，却是近几十年来随着传感器技术和精密仪器的发展才得以实现。这主要是由漏磁场本身固有的复杂特性决定的：

1. 三维空间性：漏磁场是一个在三维空间中分布的矢量场，对其进行完整描述需要获取多个方向分量的数据。
2. 局部集中性：这是一个空间尺度极小的场。经验表明，漏磁场的宽度通常仅为缺陷宽度的2到5倍，这意味着检测必须在微米级别上进行。
3. 非线性特征：由于铁磁材料的磁导率μ_r本身就是磁化强度H的非线性函数，因此漏磁场也表现出强烈的非线性，这给定量分析带来了巨大挑战。

在实际测量中，霍尔（Hall）器件是应用最广泛的检测元件。现代化的扫描设备可以驱动霍尔探头在X-Y平面内做微米级的步进扫描，从而精细地绘制出漏磁场的分布图。图1便是一个典型的管壁凹坑缺陷所产生的漏磁场垂直分量（B_y）的实验测量结果。

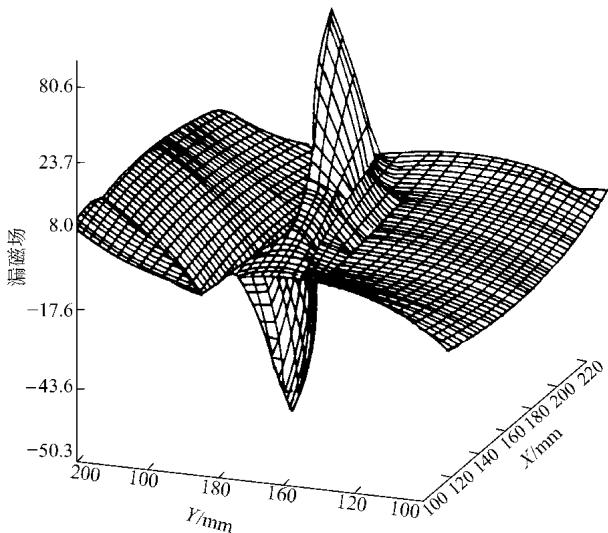图1 Atherton的实验测量结果

从图中可以清晰地看到漏磁场信号呈现出两个极性相反的峰值。这两个峰值的差值，即“峰-峰值”，在漏磁检测实践中是应用最为广泛的特征参数，通常记为 B_y(p-p) 或 H_y(p-p)，两者通过真空磁导率μ₀进行换算（B_y(p-p) = μ₀ × H_y(p-p)）。

理论计算：用数学语言描述漏磁世界

为了更深刻地理解漏磁场的内在规律，研究人员发展了多种理论计算方法，主要可以归结为解析法和数值法两大流派。

1. 解析法：优雅的简化与模型的局限

解析法的核心在于建立一个能够反映物理规律且在数学上可解的方程模型。1966年，Sheherbinin和Zastsepin提出的磁偶极子模型是该领域最早的经典尝试。该模型将缺陷简化为一对极性相反的磁偶极子，如图2所示。以一个二维矩形槽为例，其两侧被视为磁荷密度为-Q和+Q的磁极，它们在空间中任意一点 P(x,y) 产生的漏磁场可以通过矢量叠加得到：

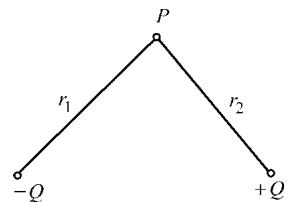图2 磁偶极子模型示意图

$$ B = B_{1} + B_{2} = /frac{-Q}{4/pi/mu_{0}r_{1}^{2}}/hat{r_1} +/frac{Q}{4/pi/mu_{0}r_{2}^{2}}/hat{r_2} $$

这里的 B₁ 和 B₂ 分别是两个磁极子产生的磁场，μ₀ 是真空磁导率，r₁ 和 r₂ 是从磁极子到P点的距离，r̂₁ 和 r̂₂ 是对应的单位矢量。

磁偶极子模型本质上是经典电磁学中静电场理论的延伸，它在一定程度上成功解释了漏磁场的空间分布特性。然而，这种高度简化的模型也存在其固有的局限性。当边界条件变得复杂，例如缺陷形状不规则时，该模型便会遭遇难以克服的障碍——无法准确确定磁偶极子的分布。事实上，磁荷的分布与材料的磁非线性、外加磁化强度以及缺陷的具体几何形状都密切相关。解析法的优雅，在复杂的工程现实面前显得力不从心。

2. 数值方法：求解复杂电磁世界的利器

漏磁场的本质是缺陷导致磁场分布的局部畸变。要从“场”的根本角度去理解它，必须求助于现代电磁学理论，其基石便是麦克斯韦方程组。其微分形式如下：

$$ /nabla /cdot D = /rho_{f} $$ $$ /nabla /times E = -/frac{/partial B}{/partial t} $$ $$ /nabla /cdot B = 0 $$ $$ /nabla /times H = J_{f} + /frac{/partial D}{/partial t} $$

其中，D 是电位移矢量，E 是电场强度，B 是磁感应强度，H 是磁场强度，ρ_f 是自由电荷密度，J_f 是自由电流密度。

要在三维空间中直接求解这个时变方程组，除了极少数特殊情况，用解析方法几乎是不可能的。为了攻克这类难题，以及力学、机械等领域的类似问题，数值方法应运而生。这些方法包括有限差分法、积分法、变分法等，其中变分法的现代形式——有限元法（Finite Element Method, FEM）——随着计算机算力的飞跃，已成为不可或缺的科学计算工具。

在漏磁场的数值计算中，有限元法展现出巨大优势：

• 几何灵活性：通过将求解区域划分为不同形状的单元（网格），可以精确地拟合任何复杂的缺陷形状和边界条件。
• 计算高效性：其生成的代数方程组具有对称正定的系数矩阵，这极大地简化了求解过程，提高了计算效率。
• 边界条件易于处理：能够方便地引入各种边界条件，简化了编程实现的复杂性。

大量的研究和实践已经证明，对于涉及材料非线性、几何形状复杂的缺陷漏磁场问题，数值计算是当前唯一切实可行的求解途径。

获取精确的漏磁场分布数据，无论是通过高精度实验还是复杂的数值模拟，都需要深厚的专业知识和强大的技术平台。这正是专业检测实验室的核心价值所在。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测漏磁检测，可靠准确。欢迎沟通交流，电话19939716636

影响缺陷漏磁场信号的关键因素

借助试验和理论计算，人们已经基本掌握了各种因素对漏磁场信号的影响规律。这对于正确解释检测信号、实现缺陷的准确定量至关重要。

1. 缺陷深度 在缺陷宽度固定的前提下，漏磁场垂直分量的峰-峰值 B_y(p-p) 与缺陷深度在一定范围内呈现出良好的线性关系。这意味着，在其他条件不变时，缺陷越深，信号幅值越大。

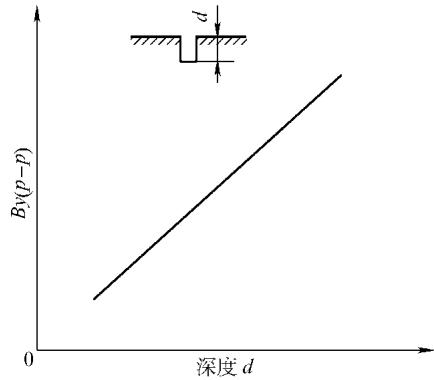图3 缺陷深度与 B_y(p-p) 的关系

2. 缺陷宽度 对于深度相同的矩形槽，在磁化条件一致时，随着宽度的增加，B_y(p-p) 值会先增大后减小。这个变化趋势的拐点位置与传感器探头的提离值（Lift-off）有关，通常在提离值约为缺陷宽度的两倍时，信号达到最大。这个规律可能会因材料和磁化状态的不同而略有差异。

3. 缺陷倾角 (α) 缺陷的倾斜角度对漏磁信号有显著影响。随着倾角从0°（平行于表面）增加到90°（垂直于表面），B_y(p-p) 值会逐渐增大。

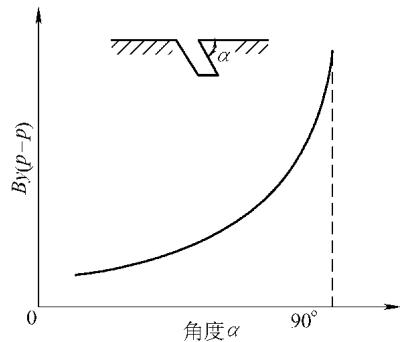图4 缺陷倾角对漏磁场的影响

4. 缺陷的埋藏深度 对于内部缺陷，即未开口于表面的缺陷，其埋藏深度与漏磁场幅值也近似成线性关系。形状和大小相同的缺陷，埋藏得越浅，其在表面产生的漏磁场信号越强。

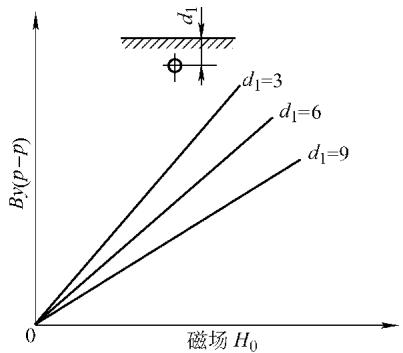图5 缺陷埋藏深度对漏磁场的影响

5. 提离值 (L) 提离值，即传感器探头表面到被测工件表面的距离，是影响信号强度的最关键因素之一。随着提离值的增大，B_y(p-p) 值会急剧下降，呈现强烈的非线性关系，其衰减速率大致遵循 1/Lⁿ 的规律。通常，缺陷越深，信号随提离值增加而衰减得越慢。

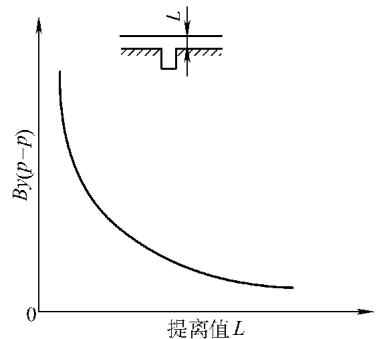图6 提离值对漏磁场的影响

6. 检测元件宽度 传感器的物理尺寸同样会影响测量结果。随着检测元件宽度的增加，测得的 B_y(p-p) 值会下降，并且信号的两个峰值会向外侧移动。这是由于较宽的传感器对其感应区域内的磁场信号存在“面积平均效应”，导致信号被平滑和展宽。

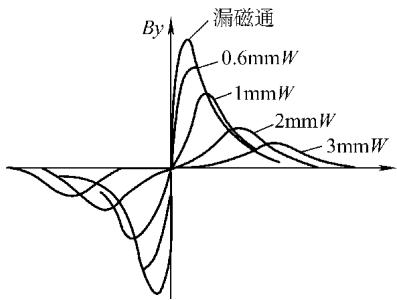图7 检测元件宽度（W）的影响

在实际的无损检测工作中，准确评估这些耦合因素对信号的综合影响，是实现缺陷精确定量的关键。如果您在实际工作中也面临类似的无损检测挑战，我们非常乐意与您一同探讨解决方案。