在工业管道、换热管等关键部件的质量控制中，对薄壁管纵向缺陷的精确检测至关重要。超声波水浸法因其耦合稳定、灵敏度高的特点，成为此项任务中的主流技术。然而，要实现对内外壁微小缺陷的可靠检出，从探头选择到工艺参数设定，每一步都充满了技术挑战。本文将深入探讨水浸法中平探头与聚焦探头的应用原理，并重点解析实现高效检测所需的核心参数优化。
平探头（非聚焦探头）是超声检测中的基础工具，其在水浸法检测管材时的基本操作与原理相对直观。
检测设置的核心在于，使待检管材外壁与作为耦合剂的水充分接触，而管内保持中空。初始校准时，将探头置于管材正上方（图1中A位置），使其声束中心线对准管子轴线。在此位置，由于声束垂直入射，管子外壁的界面反射回波最强，同时在管壁内能观察到最多次的底面回波。
完成对中后，将探头沿垂直于管轴的方向平移至B位置，产生一个偏心距 a。这个简单的机械位移，结合管材的外径 D，便可确定超声波在水中的入射角 α。
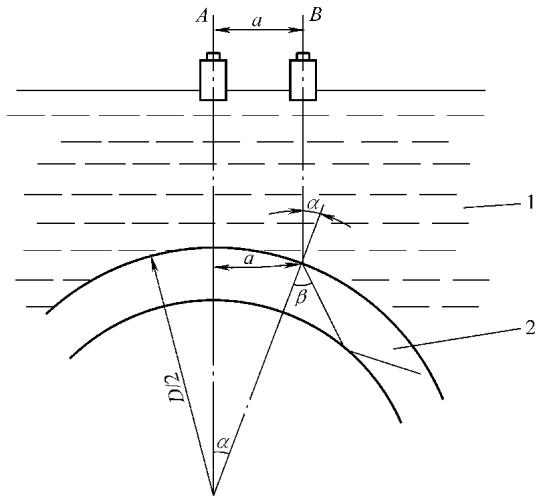图1 折射角的几何确定法
其几何关系如下：
$$ /sin /alpha = /frac{2a}{D} $$
一旦入射角 α 确定，根据斯涅尔定律（Snell’s Law），即可计算出声波在管壁中折射后产生的横波折射角 β：
$$ /sin /beta = /frac{C_{t管}}{C_{l水}}/sin /alpha $$
式中，C<sub>l水</sub> 为水中纵波声速（约1500 m/s），C<sub>t管</sub> 为管材中的横波声速（例如，钢中约为3230 m/s）。
在实际操作中，理论计算往往难以一步到位。更行之有效的方法是利用与被检管尺寸、材质相同的对比试样。通过在试样内外壁预制电火花人工标准缺陷（如刻槽），边旋转管材，边缓慢调整探头的偏心距，直至内外壁人工缺陷的回波信号幅度大致相等，此时探头的位置即为最佳检测位置。
水浸法虽然耦合稳定，但相比于传统的接触法（如使用有机玻璃斜楔），其声束扩散问题更为突出。原因在于水中的纵波声速（~1500 m/s）远低于有机玻璃（~2730 m/s）。根据斯涅尔定律，这意味着在水中要获得相同的折射角，需要一个更大的入射角范围变化。
这种固有的物理特性导致平探头发出的平行声束在进入管壁时，不同部分的入射角存在差异：
为了克服声束扩散、抑制杂波并提升检测信噪比，线聚焦探头成为了更优越的选择。
聚焦探头通过其特殊的声学透镜设计，能将声能汇聚到特定区域，从而显著改善声束形态，是高质量薄壁管检测的核心技术。
理想的聚焦探头配置旨在让声束以近乎一致的入射角射入管壁，从而在管壁内产生单一、纯净的横波。其配置思路如图2所示：
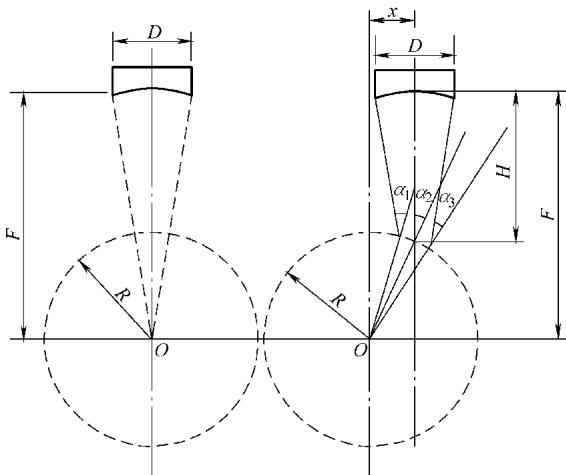图2 聚焦探头的理想配置示意图 (a) 对中状态 (b) 施加偏心距 x 后的入射状态
首先，可以想象一个以探头焦点为圆心、待检管外径为半径的虚拟圆。当探头与管材对中时，焦点位于管材轴线上方（图2a）。实际检测时，将探头平移一个偏心距 x（图2b）。在这种几何配置下，可以推导出，声束边缘的入射角 α₁ 与 α₃ 相等。这意味着整个声束以一个非常集中的角度范围入射到管壁，有效抑制了折射角的发散，确保了在管壁中传播的是纯净的横波，同时也极大地提高了检测灵敏度。
要实现理想的聚焦效果，一系列关键参数的精确计算与选定是必不可少的。
x 的选定偏心距的选取目标是：在管壁中只激发横波，并确保该横波能够传播至管材内壁，以实现全壁厚覆盖。
这需要满足一系列基于斯涅尔定律的边界条件：
$$ /frac{/sin/alpha}{C_{l水}} = /frac{/sin/beta_{l}}{C_{l管}} = /frac{/sin/beta_{t}}{C_{t管}} $$
β<sub>l</sub> 需 ≥ 90°。这要求水中的入射角 α 必须满足：
$$
/alpha /geq /arcsin /frac{C_{l水}}{C_{l管}}
$$β<sub>t</sub> 必须满足几何关系：
$$
/sin /beta_{t} /leq /frac{r}{R}
$$
结合斯涅尔定律，这对应于水中的入射角 α 需满足：
$$
/alpha /leq /arcsin /left(/frac{C_{l水}}{C_{t管}}/frac{r}{R}/right)
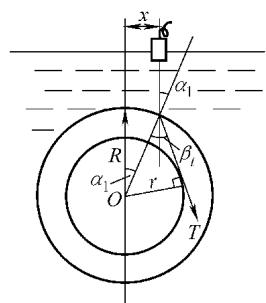$$
图3 横波在管壁中的传播路径与偏心距 x 的关系
综合以上条件，理想的入射角 α 必须在一个精确的区间内。这个角度区间直接对应探头中心线与管中心线的偏心距 x 的范围：
$$ /frac{C_{l水}}{C_{l管}} /leq /frac{x}{R} /leq /frac{C_{l水}}{C_{t管}}/frac{r}{R} $$
以钢管为例，代入声速值（C<sub>l水</sub>≈1500 m/s, C<sub>l管</sub>≈5850 m/s, C<sub>t管</sub>≈3230 m/s），可得偏心距 x 的实用范围：
$$ 0.251R /leq x /leq 0.458r $$
其中 R 为管外径，r 为管内径。这个公式明确指出，最佳偏心距不仅与材料声速有关，还与管材的具体尺寸（径厚比）紧密相关。任何偏离这个窗口的设置，都可能导致漏检或误判。
θ 的要求聚焦角 θ（或称孔径角）决定了聚焦声束的汇聚程度。为了确保整个声束的入射角都落在上述的理想区间内，聚焦角 θ 必须足够小。其上限由以下关系式确定：
$$ /theta /leq /arccos /left[/frac{/sin(/alpha_{2} - /Delta/alpha)}{/sin/alpha_{2}}/right] $$
其中，α₂ 是最大入射角，Δα 是允许的入射角变化范围。对于水浸法检测，该公式可简化为一个更具指导性的经验关系：
$$ /theta /leq /arccos /left(0.55/frac{R}{R - r}/right) $$
这里 R-r 即为管壁厚度。这表明，管材的壁越薄（R/t越大），对探头聚焦角的要求就越严格。
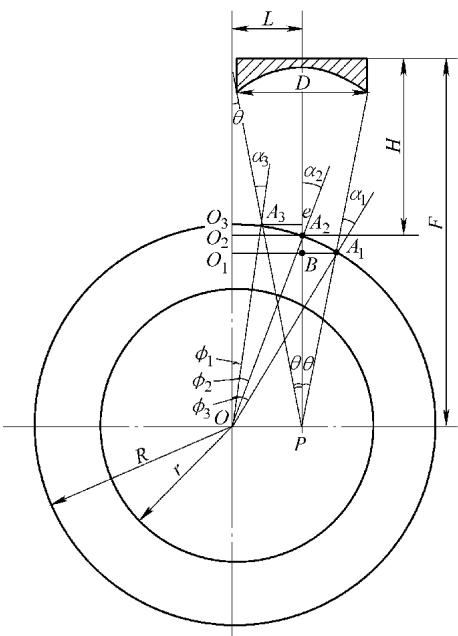图4 聚焦声束在管壁中的声程示意
聚焦声束的宽度直接影响检测的覆盖范围和抗干扰能力。
t。通过调整入射角 α 和折射角 φ，可以确保内外壁的扫查深度 h<sub>o</sub> 和 h<sub>i</sub> 之和等于壁厚 t。这需要精确计算中心射束的最大折射角 φ<sub>cmax</sub>，其与管材的外径/壁厚比（D/t）关系如图6所示。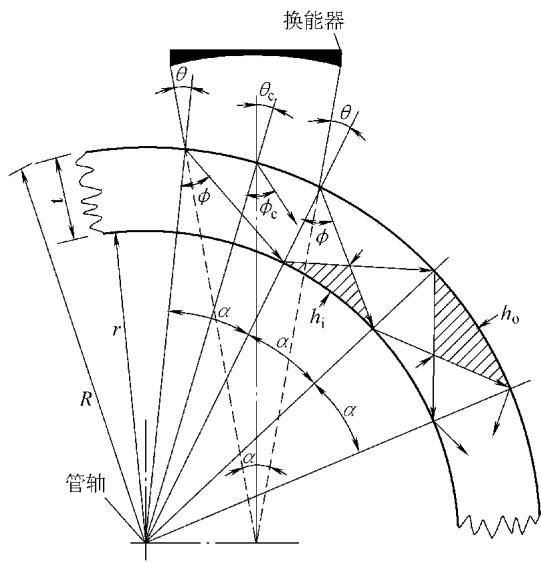
图5 通过声束旋转实现全壁厚覆盖的几何模型
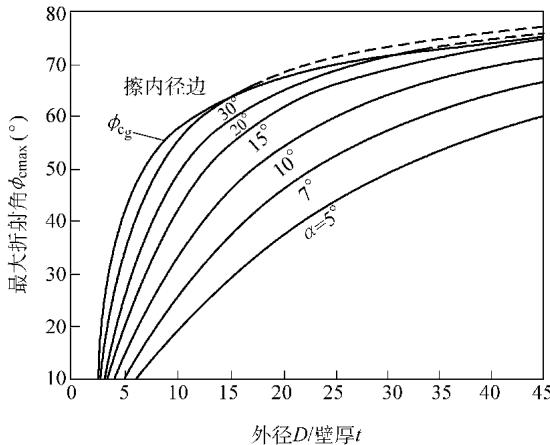图6 中心射束最大折射角与外径/壁厚比的关系
d<sub>e</sub> 必须小于一个临界值。或者，如果声脉冲足够窄（通过使用高频、高阻尼探头实现），即使声束较宽也能分辨出多次回波，避免干扰。声脉冲宽度 W 应满足：
$$
W < /frac{2t}{C_s/cos/theta}
$$
其中 C<sub>s</sub> 是管壁中的横波速度。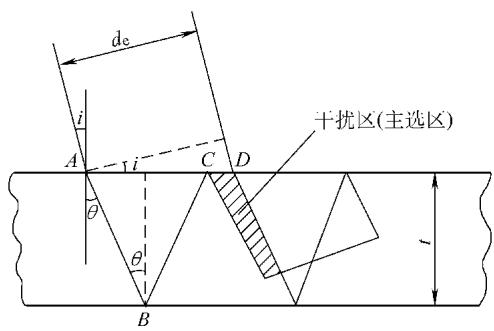
图7 声束斜射入薄板时干扰区的形成
对于壁厚极薄的管材，甚至需要利用聚焦探头的焦斑（焦栓）部分入射管壁，并确保折射后的焦斑长度能覆盖整个声程，同时宽度满足要求。
这一系列复杂的参数优化过程，涉及声学、几何学和材料科学的综合应用。要获得一张信噪比高、结果可靠的图谱，对样品制备、设备参数配置都有极高要求。这正是专业检测实验室的核心价值所在。
精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测管材超声波无损检测，可靠准确。欢迎沟通交流，电话19939716636
在确定了探头及其声场参数后，最后的环节是设定机械扫查的工艺参数，以确保对整个管材表面进行无遗漏的检测。通常采用螺旋式扫查，并进行两个相反方向的扫查，以确保对不同方向的纵向缺陷都有最高的检出率。
P螺距 P 指的是管材每旋转一周，探头沿轴向移动的距离。为保证不错过任何长度大于 N 的缺陷，螺距必须小于声束在管壁中的有效轴向长度 B<sub>-3dB</sub> 与 N 的差值。
$$ P /leq |N - B_{-3dB}| $$
B<sub>-3dB</sub> 通常指声束能量下降3分贝时的宽度，代表了声束的核心有效区域。
n管材的旋转速度 n 受到检测系统脉冲重复频率 f 的限制。转速过快会导致单位面积接收到的脉冲数过少，可能造成缺陷信号的丢失。其上限由下式决定：
$$ n /leq /frac{f /cdot B_{-3dB}}{M /cdot /pi D} $$
式中，D 是管材外径，M 是一个安全系数。M 的取值取决于报警和记录方式：对于单次脉冲即可触发报警的系统，M 可取 1~2；如果系统采用累计报警机制（需要多次缺陷脉冲叠加以防误报），则 M 值需要适当增大，以确保有足够多的脉冲击中缺陷。
通过对探头物理特性、声场参数和机械扫查工艺的系统性优化，超声波水浸法能够对薄壁管的纵向缺陷实现高效、精确的质量控制。
首页
检测领域
服务项目
咨询报价