深度解析涡流检测：线圈阻抗的物理模型与分析方法

在涡流无损检测（ECT）领域，检测线圈的阻抗变化是揭示材料内部信息的关键窗口。无论是微小的裂纹、材料电导率的波动，还是几何尺寸的差异，最终都会以线圈阻抗的特定变化形式呈现出来。因此，深刻理解线圈阻抗的物理模型及其在不同检测场景下的响应特性，是每一位无损检测工程师和科研人员的核心技能。本文将从基础的电路模型出发，系统性地剖析单线圈、耦合线圈乃至各类探头的阻抗特性，并阐明归一化、特征频率等关键概念在实际分析中的应用。

1. 线圈阻抗的基础模型与归一化

1.1 单线圈的等效电路与阻抗

为了进行理论分析，涡流检测中的单个线圈可以被简化为一个理想的电阻（R）与电感（L）的串联电路，其匝间的分布电容通常被忽略。

图1 涡流检测中单个线圈的等效电路

当一个正弦交流电 i = I_msin(ωt) 流过该电路时，根据基尔霍夫电压定律，总电压为电阻上的电压与电感上的电压之和：

V₀ = V_R + V_L = I_mRsin(ωt) + ωLI_msin(ωt + π/2)

在工程分析中，使用相量法更为直观：

V = IR + jωLI = I(R + jX_L)

由此，电路的交流阻抗 Z，即总电压与电流之比，可以表示为一个复数：

Z = V/I = R + jX_L

在这个复数中，实部 R 代表线圈的电阻，虚部 X_L = ωL 代表其感抗。在复阻抗平面上，电阻和感抗构成一个直角三角形，阻抗的模和相位角的关系如下：

|Z| = √(R² + X_L²), tanθ = X_L/R

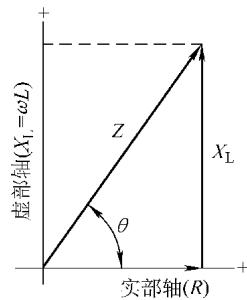
图2 复阻抗平面的阻抗表示

在涡流检测实践中，一个至关重要的基准是空线圈阻抗。这是指当检测线圈远离任何导电或导磁材料时测得的阻抗，我们用 Z₀ 表示：

Z₀ = R₀ + jX_L0 = R₀ + jωL₀

其中 R₀ 和 L₀ 分别是空线圈的电阻和自感。通常，为了产生足够强的磁场并控制热损耗，涡流线圈会绕制很多匝，这使得其感抗 ωL₀ 远大于其自身电阻 R₀。因此，在很多分析中可以进行近似：

Z₀ ≈ ωL₀

这个近似值 Z₀ 或 ωL₀，成为了一个标准化的“尺子”，在阻抗测量和复阻抗平面图分析中，用作归一化处理的基准参数，以消除不同线圈或设备间的固有差异。

1.2 耦合线圈：探头与试件的相互作用

当检测线圈（原线圈）靠近导电试件时，电磁感应定律开始发挥作用。试件中感生出的涡流，其本身会产生一个反向磁场，这个磁场反过来又会影响原线圈。从电路的角度看，这个过程可以完美地类比为两个耦合线圈的互感模型：检测线圈是原线圈，而导电试件则等效于一个短路的副线圈。

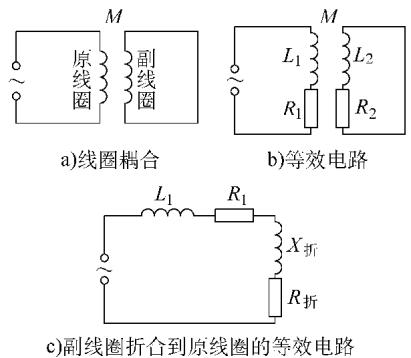
图3 线圈耦合的等效电路

副线圈（试件）的阻抗会通过互感“折合”到原线圈电路中，使得原线圈的阻抗发生变化，形成一个视在阻抗 Z。

Z = R + jX R = R₁ + R_H = R₁ + ( (X_M²) / (R₂² + X₂²) ) * R₂ X = X₁ + X_H = X₁ + ( (-X_M²) / (R₂² + X₂²) ) * X₂

• R₁, X₁: 原线圈的电阻和感抗
• R₂, X₂: 副线圈（试件）的等效电阻和感抗
• X_M = ωM: 互感抗

通过监测原线圈视在阻抗的变化，我们就能反推出试件的电磁特性。如图4所示，视在电阻 R 和视在感抗 X 的变化轨迹在阻抗图上呈现为一条半圆形曲线。

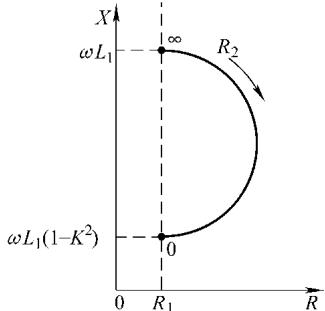
图4 原线圈的视在阻抗平面图

为了消除原线圈自身电阻 R₁ 和测试频率 ω 对曲线位置的影响，便于在不同条件下进行比较分析，我们引入了归一化处理。归一化阻抗图的横轴为 (R - R₀)/ωL₀，纵轴为 ωL/ωL₀。这里的 R₀ 和 L₀ 就是前述的空线圈参数。经过归一化后，不同线圈、不同频率下的测试结果便可以在同一个标准框架下进行比较。

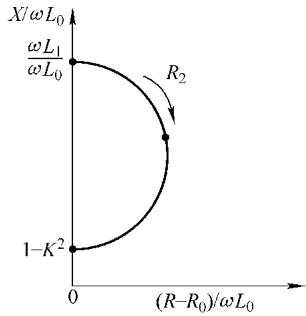
图5 归一化后的耦合线圈阻抗平面图

总结来说，当检测线圈靠近导电试件时：

1. 感抗减小：试件中的涡流产生的反向磁场削弱了原磁场，导致线圈的总磁通量减少，感抗 X 下降。
2. 电阻增大：涡流在试件中流动会因材料电阻而产生热损耗（焦耳热），这部分能量损失在等效电路中表现为原线圈的视在电阻 R 增大。电阻的变化量为 (R - R₀)。

2. 放置式线圈的阻抗特性

放置式线圈（或称探头式线圈）是应用最广泛的类型，常用于平板或曲率较小的表面检测。其阻抗受多种因素的复杂影响：

• 提离效应 (Lift-off)：这是指探头与试件表面之间的距离变化。当探头提起时，与试件的磁耦合减弱，感生的涡流也随之减弱。这使得线圈的阻抗点沿着“提离曲线”向空线圈点（0, 1）移动。在非铁磁性材料检测中，空线圈点对应着感抗的最大值。反之，探头越贴近表面，耦合越强，感抗减小得越多。提离效应是涡流检测中一个主要的干扰信号源。
• 边缘效应 (Edge Effect)：当探头靠近试件边缘时，部分磁力线会“泄漏”到试件外部，无法有效地在材料中感生涡流。对于非磁性材料，这种效应在阻抗图上的表现与提离效应有相似之处。
• 其他因素：试验频率、试件电导率、试件厚度（当厚度与涡流穿透深度可比时）的任何变化，都会直接改变涡流的分布和大小，从而显著影响线圈的阻抗。

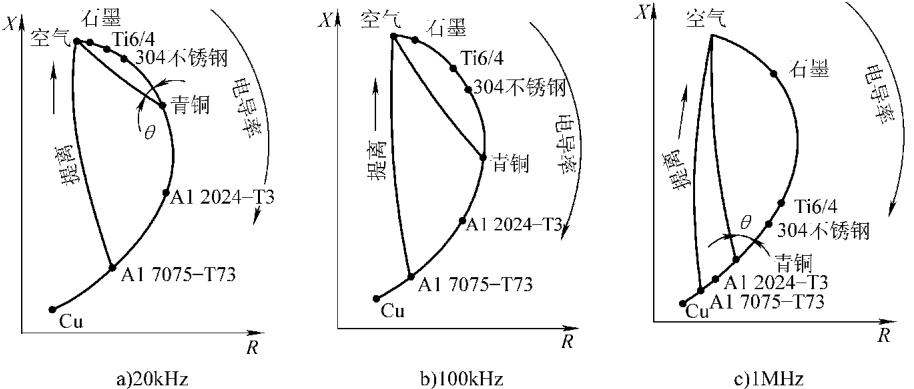
图6 频率、电导率、提离对放置线圈阻抗的影响

这些因素的叠加使得信号解读变得复杂，因此，准确分离和识别由缺陷引起的阻抗变化与由这些干扰因素引起的阻抗变化，是涡流数据分析的核心挑战。这正是专业检测实验室的核心价值所在。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测涡流无损检测，可靠准确。欢迎沟通交流，电话19939716636

3. 穿过式线圈的阻抗分析：以无限长导电圆棒为例

对于棒材、线材的在线检测，穿过式线圈是标准配置。其物理模型的分析更为复杂，通常需要借助一些关键的简化概念。

3.1 特征频率 f_g：一个标准化的参考点

动态磁场与感生电流的相互作用本质上由麦克斯韦方程组描述。对于一个被线圈环绕的均质圆柱体，该方程的解会涉及复杂的贝塞尔函数。为了简化分析，工程上引入了一个宗量 A，它将影响涡流的关键参数打包在一起：

A = (f * μ_r * σ * d²) / 5066

• f: 涡流频率 (Hz)
• μ_r: 材料相对磁导率
• σ: 材料电导率 (m/(Ω·mm²))
• d: 圆柱试件直径 (cm)

为了建立一个统一的比较基准，我们定义一个特征频率 f_g，即令宗量 A = 1 时的频率：

f_g = 5066 / (μ_r * σ * d²)

特征频率本身并非最佳测试频率，也不是频率的上下限。它的真正价值在于提供了一个包含材料和尺寸信息的“指纹”。任何实际的测试频率 f 都可以通过与 f_g 的比值 f/f_g 来进行归一化，从而使得不同规格材料的测试结果具有可比性。

f/f_g = (f * μ_r * σ * d²) / 5066

3.2 有效磁导率 μ_eff：一个巧妙的简化工具

在圆棒内部，磁场强度和涡流密度都随着离表面的距离增加而衰减，在中心处涡流几乎为零。直接计算这种非均匀分布非常困难。为此，我们引入有效磁导率 μ_eff 的概念。我们假想一个等效场景：外加磁场 H₀ 在整个截面上是均匀的，但材料的磁导率不再是其真实值，而是一个复数 μ_eff。这个μ_eff 包含了所有关于涡流场反作用的幅度和相位信息。

μ_eff = μ_eff(real) + jμ_eff(imag)

通过这种方式，复杂的场分布问题被简化为使用一个等效材料参数 μ_eff 的问题。尽管这种简化基于一系列理想化假设（如线圈场均匀、试件无限长、材料特性恒定等），在很多实际应用中，它仍然是分析穿过式线圈检测信号的强大工具。

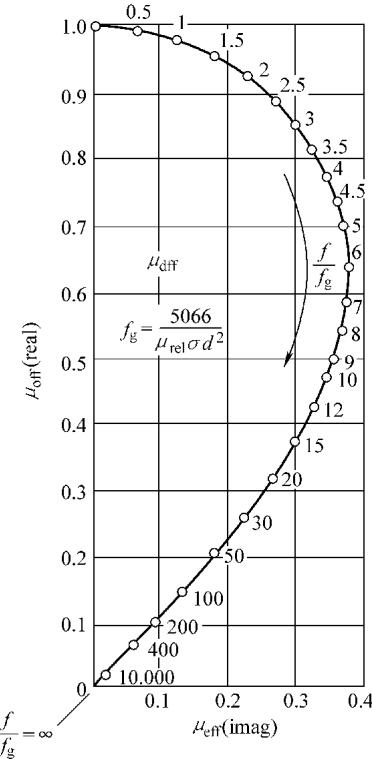
图7 实心非铁磁性圆棒在完全填充线圈时，有效磁导率的复平面图

3.3 填充因子 η：考虑实际间隙

在实际检测中，试棒直径 d 必须小于线圈内径 D，以便自由通过。这个几何关系用填充因子 η 来量化，它代表试棒截面积占线圈截面积的比例：

η = (d/D)²

填充因子直接影响耦合效率。对于非铁磁性长圆棒，归一化的检测线圈（副线圈）感应电压可以表示为：

V_sec / V₀ = 1 - η + ημ_eff

其中 V₀ 是空线圈时的电压。这个公式清晰地显示了最终信号是如何由填充因子 η 和材料的有效磁导率 μ_eff 共同决定的。

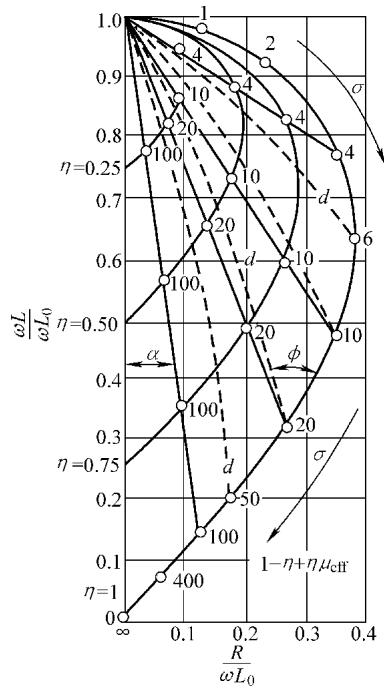
图8 含非铁磁性圆棒线圈的阻抗平面图，显示了不同填充因子下的情况

4. 管材检测：穿过式与内通过式线圈

对于管材检测，根据探头在管外还是管内，分为穿过式（外穿）和内通过式（内穿）两种情况。

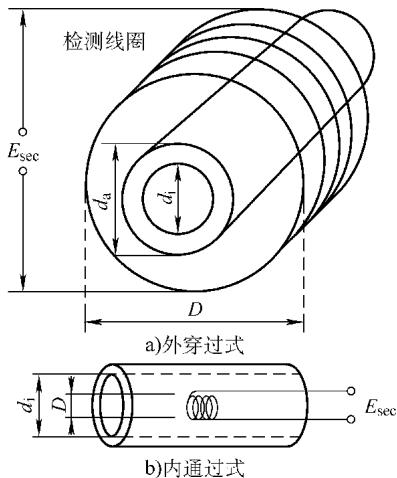
图9 用于管材涡流检测的线圈配置

填充因子的定义也相应调整：

• 外穿式: η = (d_a/D)² (d_a为管外径)
• 内穿式: η = (D/d_i)² (d_i为管内径)

4.1 薄壁管情况

薄壁管指壁厚 W 远小于管径，且涡流密度在整个壁厚上近似均匀。其特征频率 f_g 的计算公式调整为：

f_g = 5066 / (μ_r * σ * d_i * W)

其中 d_i 是管内径（cm），W 是壁厚（cm）。下图展示了薄壁管的有效磁导率曲线和归一化阻抗平面图。

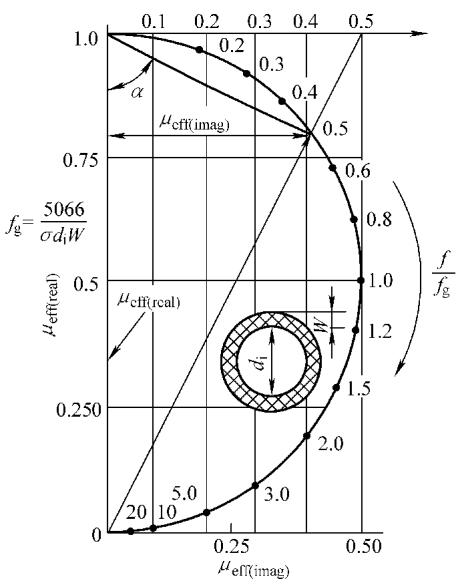
图10 非铁磁性薄壁管在 η=1 时有效磁导率与 f/f_g 的关系

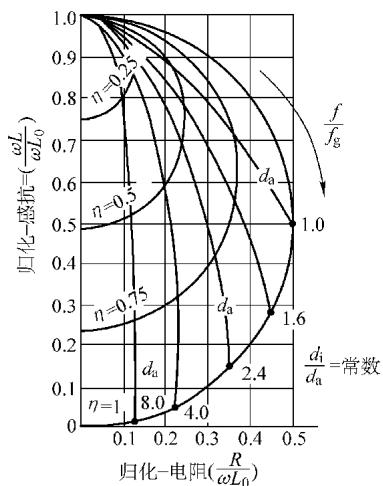
图11 外穿过式线圈非铁磁性薄壁管的阻抗平面图

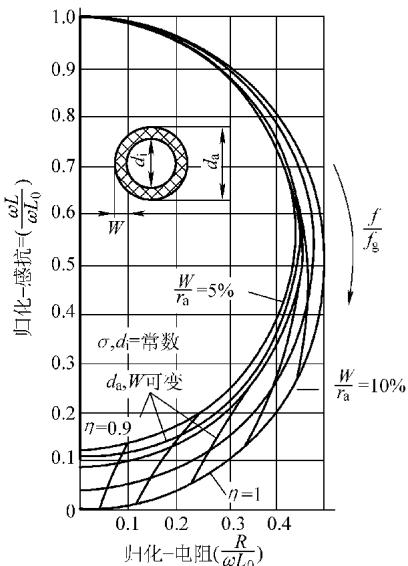
图12 内通过式线圈非铁磁性薄壁管的阻抗平面图

4.2 厚壁管情况

当管壁较厚，涡流的趋肤效应变得显著时，其阻抗特性介于薄壁管和实心棒之间。在填充因子 η=1 时，厚壁管的阻抗变化轨迹会落在下图所示的阴影区域内。该区域的外边界是薄壁管的轨迹，内边界则是实心棒的轨迹。

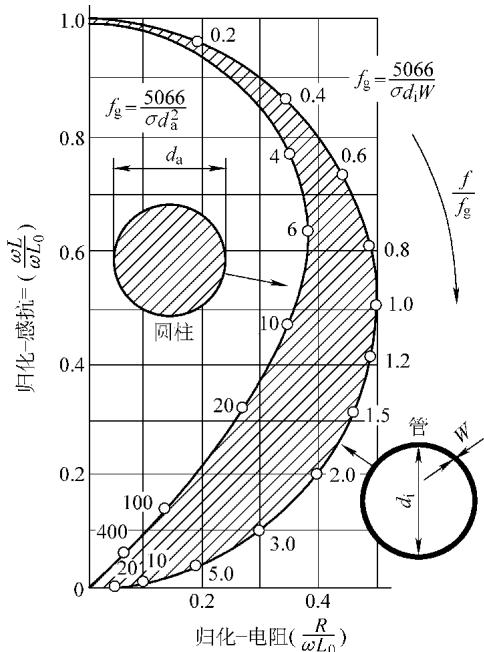
图13 厚壁非铁磁性管穿过式检测时阻抗变化的范围（阴影区, η=1）

对于厚壁管的内通过式检测，其阻抗平面图和特征频率公式如下：

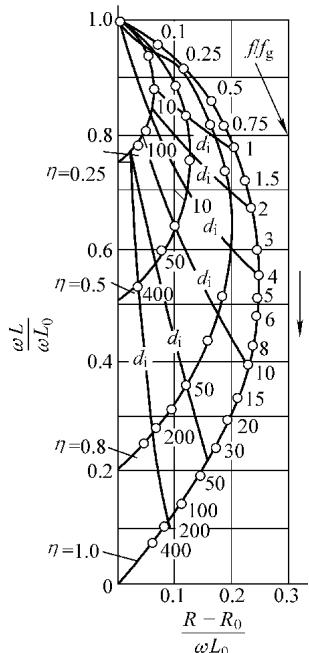
图14 厚壁非铁磁性管内通过式线圈检测的阻抗平面图

特征频率 f_g = 5066 / (μ_r * σ * d_i²)

这里的特征频率公式与实心棒类似，但使用的是管内径 d_i。

通过对这些模型的理解，检测人员可以更有效地设置检测参数、分析阻抗平面图上的信号轨迹，并最终对材料的健康状况做出准确的判断。