涡流检测作为一种重要的无损检测(NDT)方法,其应用深度与广度根植于坚实的物理学基础。要真正掌握并灵活运用这项技术,就必须回归本源,理解其背后的电磁学定律。这些定律共同描绘了激励线圈、导电材料与感应涡流之间复杂的相互作用。本文将系统梳理构成涡流检测技术的四大物理基石。
涡流的本质是在导电材料中感生出的闭合电流。因此,材料的导电能力是实现涡流检测的先决条件。
当在一段金属导体两端施加电压 U 时,内部的自由电子会定向移动,形成电流 I。这种关系由我们熟知的欧姆定律描述:
I = U / R
其中,R 是导体的电阻(Ω)。
对于一块均质材料,其电阻 R 与几何形状和内在属性相关。它与导体长度 L 成正比,与横截面积 S 成反比,其比例系数便是材料的固有属性——电阻率 ρ。
R = ρ * (L / S)
电阻率 ρ (Ω·m) 是衡量材料阻碍电流通过能力的物理量。在涡流检测领域,我们更常使用其倒数——电导率 σ (S/m),它直观地反映了材料导电的难易程度。
在工程实践中,为了方便比较,常引入一个相对单位:IACS(国际退火铜标准)。该标准将 20°C 时高纯度退火铜的电导率定义为 100% IACS。其他材料的电导率则通过与该基准的电阻率进行比较来表示:
σ_x (% IACS) = (标准退火铜电阻率 / 待测金属电阻率) × 100
从表1可以看出,不同金属、合金乃至同种金属经过不同热处理或冷加工工艺后,其电导率存在显著差异。例如,退火铜与冷拉铜的电导率就有明显不同。这种差异正是涡流技术能够用于材料分选、热处理状态验证以及缺陷检测的物理依据。
表1:常用金属在20°C时的电阻率、温度系数和电导率
| 金 属 | 20℃时的电阻率/μΩ·cm | 温度系数20℃ | 电 导 率 |
|---|---|---|---|
| %IACS | |||
| 铝 | 2.824 | 0.0039 | 61.05 |
| 锑 | 41.7 | 0.0036 | 4.13 |
| 砷 | 33.3 | 0.0042 | 5.18 |
| 铋 | 120 | 0.004 | 1.44 |
| 黄铜 | 7 | 0.002 | 25 |
| 镉 | 7.6 | 0.0038 | 22 |
| 高电阻铁镍合金 | 87 | 0.0007 | 2.0 |
| 钴 | 9.8 | 0.0033 | 18 |
| 康铜 | 49 | 0.00001 | 3.5 |
| 铜(退火) | 1.7241 | 0.00393 | 1.0×102 |
| 铜(冷拉) | 1.771 | 0.00382 | 97.35 |
| 气体碳 | 5000 | -0.0005 | 0.03 |
| 德银(18%Ni) | 33 | 0.0004 | 5.2 |
| 金 | 2.44 | 0.0034 | 70.7 |
| 铁(99.98%纯) | 10 | 0.005 | 17 |
| 铅 | 22 | 0.0039 | 7.8 |
| 镁 | 4.6 | 0.004 | 38 |
| 锰铜(锰镍铜合金) | 44 | 0.00001 | 3.9 |
| 汞 | 95.783 | 0.00089 | 1.8 |
| 钼(拉拔) | 5.7 | 0.004 | 30 |
| 蒙乃尔合金 | 42 | 0.002 | 4.1 |
| 镍铬合金 | 100 | 0.0004 | 1.72 |
| 镍 | 7.8 | 0.006 | 22 |
| 钯 | 11 | 0.0033 | 16 |
| 磷青铜 | 7.8 | 0.0018 | 22 |
| 铂 | 10 | 0.003 | 17 |
| 银 | 1.59 | 0.0038 | 108 |
| 锰钢 | 70 | 0.001 | 2.5 |
| 钽 | 15.5 | 0.0031 | 11.1 |
| 西罗铜铝锰合金 | 47 | 0.00001 | 3.7 |
| 锡 | 11.5 | 0.0042 | 15.0 |
| 钨(拉拔) | 5.6 | 0.0045 | 31 |
| 锌 | 5.8 | 0.0037 | 30 |
| 钢(最高质量) | 10.4 | 0.005 | 16.6 |
| 钢(滚珠轴承) | 11.9 | 0.004 | 14.5 |
| 钢(平炉) | 18 | 0.003 | 9.6 |
当材料置于外磁场中时,其自身会被磁化,从而影响总磁场的分布。这一过程由磁导率 μ 来表征。
μ = B / H
式中,H 是外部磁场强度,而 B 是材料内部的总磁感应强度。
根据磁化行为,材料可分为三类:
为便于比较,通常使用相对磁导率 μ_r:
μ_r = μ / μ_0
其中 μ_0 是真空磁导率(4π × 10-7 H/m)。对于顺磁质和逆磁质,μ_r 约等于1。而对于铁磁质,μ_r 可以达到数百甚至数万。磁导率的巨大差异,使得涡流检测在区分铁磁性与非铁磁性材料时极为敏感。
电磁感应是连接激励磁场与感应涡流的桥梁,它包含三个核心现象。
当穿过一个闭合导体回路的磁通量 Φ 发生变化时,回路中就会产生感应电动势 E_i,其大小与磁通量的变化率成正比。这便是法拉第电磁感应定律,也是涡流检测的根本定律。
E_i = -dΦ/dt
负号代表了楞次定律的内涵:感应电流产生的磁场,总是阻碍引起感应电流的磁通量变化。对于一个 N 匝线圈,总感应电动势为:
E_i = -N * (dΦ/dt)
当交变电流 I 流过探头线圈时,它产生的交变磁场同样会穿过线圈自身,在线圈内激发出一个反向的自感电动势 E_L。
E_L = -L * (dI/dt)
L 是线圈的自感系数,它取决于线圈的几何形状和磁芯材料。
这是涡流检测工作的核心环节。探头线圈(线圈1)中的交变电流 I_1 产生主磁场,该磁场穿过被测工件(可视为线圈2),在其中感生出涡流(相当于 I_2)。这个涡流自身又会产生一个次级磁场,反过来作用于探头线圈,在线圈1中引起一个附加的感应电动势变化。这种相互作用就是互感。
两个线圈间的互感电动势可表示为:
E_21 = -M * (dI_1/dt)
E_12 = -M * (dI_2/dt)
M 是互感系数。两个线圈耦合的紧密程度由耦合系数 K 描述:
K = M / sqrt(L_1 * L_2)
工件中的缺陷、电导率或磁导率的变化,都会改变涡流的分布,进而改变 M 和 K,最终导致探头线圈的阻抗发生变化。这正是仪器能够捕捉到的信号。
由交变磁场在工件中产生的涡流并非均匀分布,而是呈现出一种强烈的表面聚集现象,即“趋肤效应”。涡流密度在材料表面达到最大,并随着深入材料内部的深度呈指数规律衰减。
当涡流密度衰减至表面值的 1/e(约37%)时,该深度被称为标准透入深度 δ。它可以通过下式计算:
δ = 1 / sqrt(π * f * μ * σ)
这个公式揭示了影响检测深度的三个关键参数:
f (Hz):频率越高,趋肤效应越显著,δ 越小,检测深度越浅。μ (H/m):磁导率越高,δ 越小。因此涡流在铁磁性材料中的穿透深度远小于非铁磁性材料。σ (S/m):电导率越高,δ 越小。涡流在良导体(如铜、铝)中的穿透深度较浅。在实际检测中,通常认为有效检测深度约为3个δ,因为在5δ处,涡流密度已衰减至表面值的0.7%以下,几乎可以忽略不计。
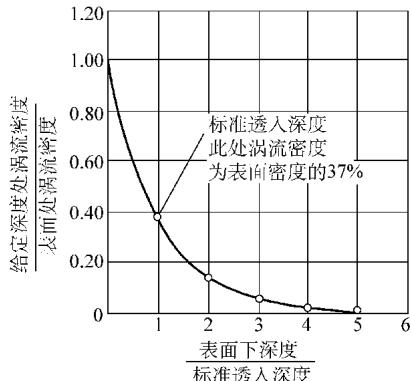 图1:平板导体中涡流密度随透入深度的关系
图1:平板导体中涡流密度随透入深度的关系
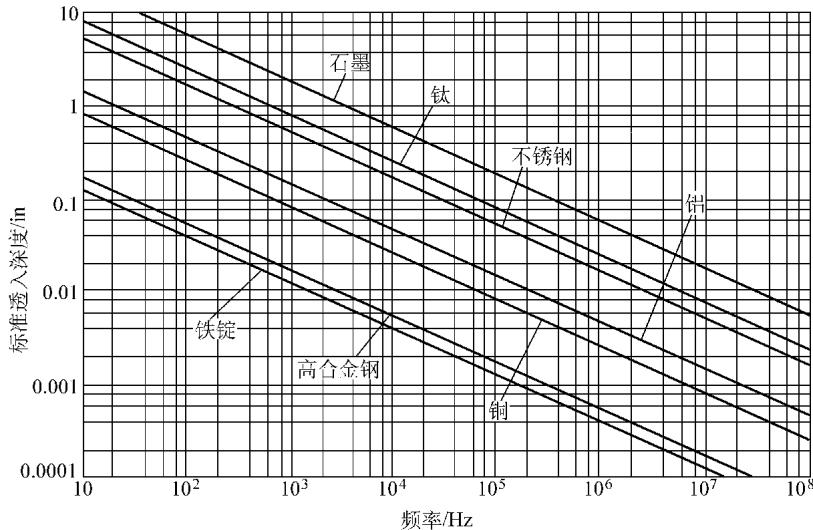 图2:不同电导率的几种金属标准透入深度与频率的关系
图2:不同电导率的几种金属标准透入深度与频率的关系
如图所示,检测频率的选择直接决定了检测深度和对表面缺陷的灵敏度。这是一个必须权衡的矛盾:高频对表面微小缺陷灵敏,但穿透能力差;低频穿透深,但对小缺陷不敏感。因此,如何根据被测件的材料属性(μ 和 σ)、预估的缺陷深度来选择最优检测频率,是涡流检测工艺开发中的核心挑战。准确获取材料的电磁参数,是制定可靠检测方案的第一步。
精工博研测试技术(河南)有限公司(原郑州三磨所国家磨料磨具质量检验检测中心),央企,国字头检测机构,专业的权威第三方检测机构,专业检测金属电导率与磁导率,可靠准确。欢迎沟通交流,电话19939716636


 首页
首页
 检测领域
检测领域
 服务项目
服务项目
 咨询报价
咨询报价