万物皆有其固有的振动特性。当一个物体受到外部激励(如敲击)时,它会以其特有的频率和模式振动,并发出声音。这种声音中蕴含了丰富的结构信息。一旦结构内部出现不连续(如裂纹),其刚度、质量分布等物理参数便会发生改变,进而导致其振动响应——也就是我们听到的声音——发生变化。这便是敲击检测法的物理基础,一门古老而直观的无损检测技术。
从古人轻叩瓷器判断其是否完好,到如今铁路工人沿途敲击检查车轮与板簧是否存在疲劳裂纹,这种方法的生命力跨越了千年。它简单、廉价且易于实施,对于大型钢构架、铁道桥梁等安全攸关的结构,仍不失为一种有效的初步筛查手段。
然而,传统的人工敲击法存在其固有的局限性。其最大的短板在于对操作人员的经验依赖性极强,检测结果受主观因素影响大,导致其可靠性和灵敏度相对较差。因此,它通常只适用于那些设计安全系数较高、对微小缺陷不甚敏感的简单刚性工件,如棒、梁、轴等。
为了确保安全,采用人工敲击法时,检测周期不宜过长。其核心原则是:必须在可检出的最小裂纹(或可能漏检的最大裂纹)扩展至临界尺寸并导致断裂之前,完成至少两次有效的检测。
随着技术的发展,电子化的敲击工具应运而生。这类设备通过微处理器精确控制机械装置进行敲击,并使用高灵敏度传感器(如加速度计)来捕捉和分析振动信号。这种方式消除了人为判读的主观性,不仅显著提升了检测的可靠性,还能实现数据的采集、显示与存储,为状态监控和趋势分析提供了可能。电子敲击法根据实施方式的不同,可分为单点激振单点测量和多点激振多点测量两种主要路径。
对于棒、梁、轴、板簧这类形状相对简单的工件,单点激振单点测量是一种高效的完整性评估方法。其核心思想是通过测量工件的自然频率(或称固有频率)和阻尼特性来判断其是否存在缺陷。
任何构件的自然频率都由其自身的物理属性决定。当构件的局部存在缺陷(如裂纹)、尺寸变化或材料性能发生改变时,其弯曲刚度 EI(E 为弹性模量,I 为截面二次矩)、单位长度质量 m、剪切刚度 Ks 或旋转惯量 ρI(ρ 为材料密度)等参数会随之变化。这些参数的微小变化与自然频率 fi 的变化之间,存在一种近似线性的关系:
Δfi ≈ ΔEI (∂fi/∂EI) + Δm (∂fi/∂m) + ΔKs (∂fi/∂Ks) + ΔρI (∂fi/∂ρI)
这个公式的意义在于,它揭示了我们可以通过追踪自然频率的偏移来反推构件的健康状况。如果存在多个局部缺陷,其引起的频率变化甚至可以进行叠加估算。
由于自然频率对尺寸变化极为敏感,该方法在制造阶段可用于检测尺寸公差要求严格的构件是否存在微小裂纹。对于航空航天领域常见的复合材料构件,如分层、脱粘、气孔等缺陷,都可以通过这种方法有效检出。
典型的检测流程如下:
为了获得最纯净的振动信号,测量时应将被测构件的支点置于所选振动模态的节点上(即振动幅度最小的位置),以最大限度地减少外部约束的影响。
以最简单的均匀棒轴向振动为例,两端自由的棒其基频振动模态的位移可以表示为: u = u0cos(πx/l) 其中,u0 是棒在 x=0 处(一端)的周期位移。
其自然频率 fi 则由以下公式决定: fi = αc / l 式中:
在结构分析中,我们有时更关心应力或应变。应变 ε 和应力 σ 可以通过位移 u 对位置 x 求导得出: ε = ∂u/∂x = -(πu0/l)sin(πx/l) σ = Eε = -E(πu0/l)sin(πx/l) (此处假设阻尼为零,这在大多数实际应用中是可接受的简化)
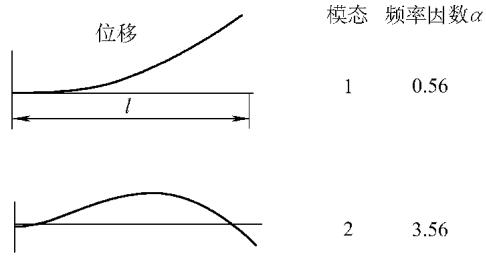
从下图可以看出,不同边界条件下,棒的轴向振动位移模态和应变(应力)模态存在显著差异。位移的节点(位移为零)往往是应变(应力)的峰值点。
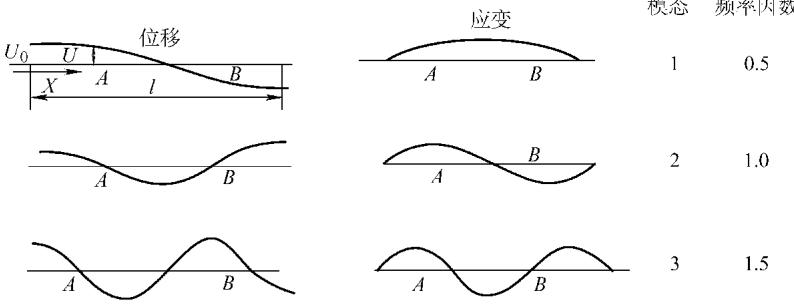
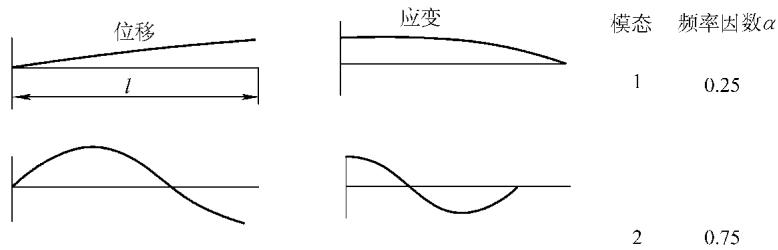
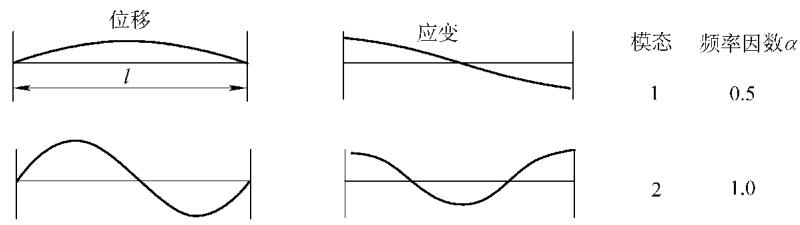
在实际工程中,弯曲振动更为常见。其运动微分方程和自然频率公式如下: ρA (∂2ν/∂t2) = -EI (∂4ν/∂x4) fi = (α/l2)(EI/ρA)1/2 其中,ν 是垂直于构件平面的位移,A 是截面积。
下图展示了两种典型边界条件下的弯曲振动模式。例如,航空发动机叶片的振动就可以近似为一端固定的悬臂梁模式。
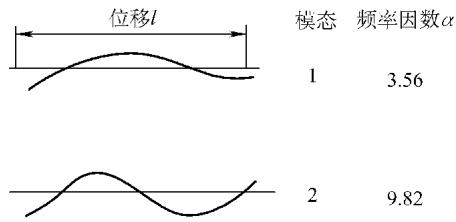
一个完整的检测程序通常按以下步骤建立:
这种方法的检测效果很大程度上依赖于整批构件的一致性。如果构件的制造公差控制得很好,那么由缺陷引起的微小频率变化就更容易被识别出来。
当面对复合材料立体网格结构这类复杂构件时,单点测量就显得力不从心了。此时,需要采用多点激振多点测量的方法,通过监测一组特定振动模态的自然频率及其模式的对称性变化,来反映损伤对结构的影响。
为了精确捕捉由微小损伤引起的变化,整个试验过程必须严格控制环境因素(如安装方式、环境温度)的影响。
以复合材料网格结构为例,其检测流程如下:

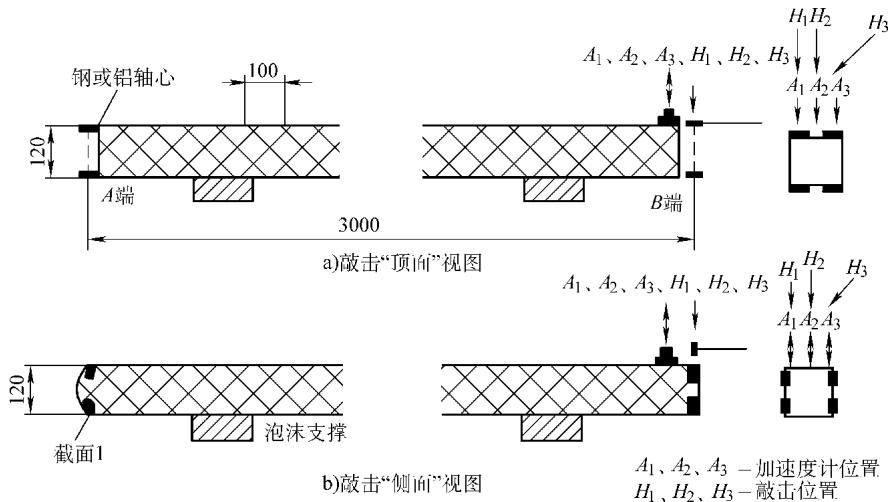
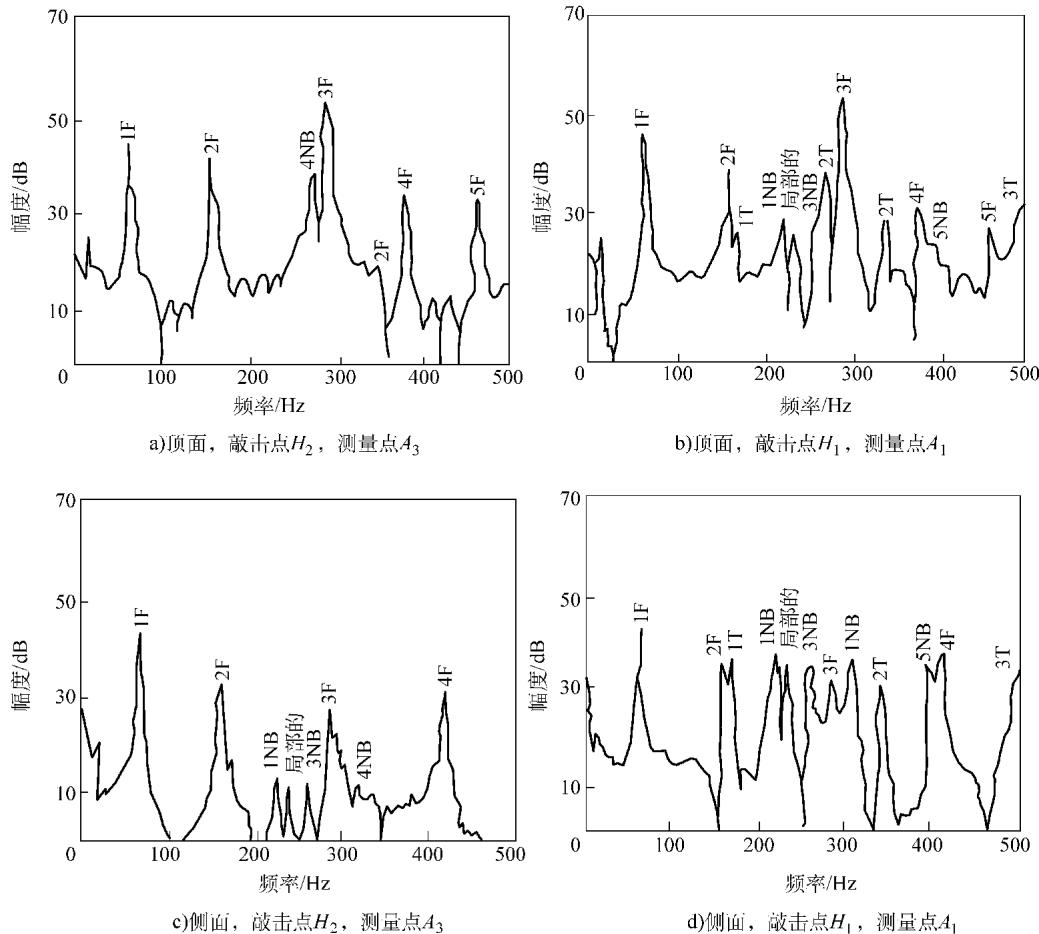
模态选择:根据激励强度、信号清晰度和灵敏度,从众多模态中筛选出最适合用于无损检测的模态。例如,最终可能选择8个在0~500Hz范围内清晰、易测的模态:1FF, 4FF, 5FF, 1FS, 4FS, 2T, 3T, 5NB。
检测、损伤与再检测:对一批样件(如12个)在不同温度下(如10°C, 20°C, 30°C)测量基准频率,并评估其一致性(见表1)。然后对部分样件施加各种人工可控损伤(见表2),再重新测量其频率,记录频率的变化量(见表3)。
表1:单件和整批频率测量的一致性
| 模态 | 构件6自然频率/Hz | 构件7四次测量的变化(%) | 构件6~12自然频率平均值/Hz | 构件6~12与平均值的最大偏差①(%) |
|---|---|---|---|---|
| 1FF | 62 | 0.4 | 61.61 | 1.4 (0.86) |
| 2FF | 159 | — | 158.04 | 1.1 (1.74) |
| 3FF | 272 | — | 282.5 | 6.1 (17.2) |
| 4FF | 377 | 0.6 | 379.66 | 1.6 (6.1) |
| 5FF | 460 | 0.3 | 463.59 | 1.6 (7.4) |
| 1FS | 62 | 0.8 | 61.36 | 1.5 (0.92) |
| 2FS | 160 | — | 158.4 | 0.9 (1.43) |
| 3FS | 285 | — | 284.92 | 0.9 (2.56) |
| 4FS | 417 | 0.1 | 416.79 | 0.8 (3.33) |
| 2T | 342 | 0 | 342.83 | 0.5 (1.71) |
| 3T | 497 | 0.1 | 500.19 | 0.6 (3.0) |
| 5NB | 404 | 0.3 | 404.46 | 0.7 (2.83) |
| 6NB | 516 | — | 517.5 | 0.7 (3.62) |
| ① 括号内为最大偏差频率,单位是 Hz |
表2:复合材料构件的规格和所受损伤
| 构件号 | 缠绕方法 | 轴心金属 | 质量/kg | 损伤位置①/100mm | 损伤说明 |
|---|---|---|---|---|---|
| 1 | 机械 | 钢 | 4.935 | 4.20 | 贯穿(轴向)弦杆件切割一半 |
| 2 | 机械 | 钢 | 4.86 | 12.27 | 去掉弦杆 |
| 3 | 机械 | 铝 | 4.65 | 2.24 | 贯穿弦杆件切割一半 |
| 4 | 机械 | 钢 | 5.1 | 4.20 | 贯穿弦杆件切割1/4 |
| 5 | 机械 | 铝 | 4.41 | — | 无损伤 |
| 6 | 手工 | 铝 | 4.8 | — | 无损伤 |
| 7 | 手工 | 铝 | 4.81 | 4.20 | 去掉拉条 |
| 8 | 手工 | 铝 | 4.825 | 5.20 | 切割弦杆件并用树脂和玻璃纤维修理 |
| 9 | 手工 | 铝 | 4.75 | 4~5、19~20 | 弦杆与拉条连接处烧坏 |
| 10 | 手工 | 铝 | 4.78 | 5、21 | 弦杆用锉擦伤 |
| 11 | 手工 | 铝 | 4.75 | 5~6、20~21 | 弦杆与拉条连接处多次冲击 |
| 12 | 手工 | 铝 | 4.75 | 1 | 端头压伤 |
| ① 损伤位置指与 A 端的距离。 |
表3:构件损伤引起频率变化
| 模态 | 1FF | 2FF | 3FF | 4FF | 5FF | 1FS | 2FS | 3FS | 4FS | 5NB | 2T | 6NB | 3T | ΣΔf | ΣΔf/f₀(%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 基准频率①f₀/Hz | 62 | 159 | 272 | 377 | 460 | 62 | 160 | 285 | 417 | 404 | 342 | 516 | 497 | ||
| 构件号 | 频率变化②Δf/Hz | ||||||||||||||
| 1 | 1.0 | -0.7 | 1.0 | 0.5 | 1.1 | 0.5 | 3.5 | -0.7 | -1.3 | 1.0 | 0.6 | -0.2 | 0.1 | 6.4 | 5.2 |
| 2 | — | — | — | — | — | — | — | — | — | — | -6.6 | -9.0 | 1.8 | -13.8 | -4.2 |
| 3 | 0.9 | -2.0 | -0.5 | -1.7 | -1.3 | 0.3 | -0.3 | 0.5 | 0.2 | — | -0.2 | -0.6 | -0.5 | -5.2 | -0.5 |
| 4 | 0.4 | -1.6 | -8.6 | -11.1 | -8.9 | 0.4 | -1.6 | -0.7 | 3.9 | -0.9 | -2.5 | -4.4 | -8.0 | -43.3 | -13.4 |
| 5 | 0.3 | -2.5 | 0.1 | 0.1 | -0.8 | 0.5 | 2.5 | — | 0.1 | 1.5 | 0.6 | 0.5 | 1.5 | 4.4 | 2.2 |
| 6 | 0.5 | -0.3 | 0.9 | 0.7 | 0.7 | 0.3 | 0.5 | 0.5 | 0.2 | 0.9 | -0.2 | -0.2 | 1.8 | 6.4 | 2.7 |
| 7 | 0.6 | -0.1 | 1.4 | 1.7 | 2.6 | 0.2 | -1.8 | -1.8 | -4.4 | -0.7 | -10.4 | -0.7 | -12.6 | -32.3 | -8.2 |
| 8 | 0.4 | 0.4 | 1.7 | 1.7 | 3.4 | 0.7 | -0.4 | 0.9 | 0.5 | 1.0 | 1.5 | 0.7 | 2.2 | 14.7 | 5.3 |
| 9 | 0.3 | -0.2 | 2.7 | 2.3 | 3.3 | 0.3 | 0.6 | 1.6 | 1.0 | 1.9 | 1.1 | 1.1 | 2.0 | 18.0 | 5.7 |
| 10 | 0.4 | -0.5 | -0.7 | -1.2 | -1.8 | 0.4 | 0.5 | 0.7 | 1.3 | 0.4 | 0.8 | 0.0 | 1.5 | 1.6 | 1.3 |
| 11 | 0.6 | 0.4 | 1.6 | -0.9 | -1.5 | 0.6 | -0.6 | 0.4 | 1.0 | 0.7 | 1.0 | 0.5 | 1.7 | 5.7 | 3.2 |
| 12 | 0.6 | -0.6 | -0.7 | 4.9 | -9.4 | 0.6 | -0.2 | 0.5 | -0.1 | -1.6 | 0.1 | -1.5 | -0.6 | -17.8 | -2.7 |
| ① 为6号构件的基准频率。 ② 频率变化是同一构件经校正温度效应后与基准频率的比较;最后两列为频率变化的和以及频率变化百分比 (Δf/f₀) 的和。 |
表4:平均失真系数
| 构件号 | 弯曲模态的平均失真系数① | 扭转模态的平均失真系数② | 所有模态的平均失真系数 |
|---|---|---|---|
| 1 | 40.0 | 66.6 | 50.1 |
| 2 | 29.4 | 45.6 | 36.8 |
| 3 | 11.1 | 17.0 | 12.9 |
| 4 | 39.4 | 25.9 | 33.3 |
| 5 | 8.9 | 6.0 | 8.3 |
| 6 | 9.7 | 29.5 | 17.6 |
| 7 | 10.9 | 35.0 | 20.5 |
| 8 | 7.6 | 26.2 | 15.0 |
| 9 | 7.9 | 12.8 | 9.9 |
| 10 | 5.6 | 9.5 | 8.0 |
| 11 | 4.8 | 7.8 | 5.6 |
| 12 | 10.2 | 19.9 | 14.1 |
| ① 弯曲模态失真系数 = 100(A₁ - A₂) / (A₁ + A₂) ② 扭转模态失真系数 = 100(A₁ + A₂) / (A₁ - A₂) |
表5:两种检测方法的比较
| 构件号 | 损 伤 | 用基线规则评定损伤② | ∑△f(见表3) | 失真系数(见表4) |
|---|---|---|---|---|
| i | ii | iii | ||
| 1 | 弦杆切割1/2 | — | — | × |
| 2 | 弦杆切割 | × | × | × |
| 3 | 弦杆切割1/2 | × | × | × |
| 4 | 弦杆切割1/4① | × | × | × |
| 5 | 无 | — | — | — |
| 6 | 无 | — | — | × |
| 7 | 拉条切断 | × | × | × |
| 8 | 弦杆切断并修理 | — | — | — |
| 9 | 触头烧坏 | — | — | — |
| 10 | 触头磨损 | — | — | × |
| 11 | 触头冲击 | — | — | × |
| 12 | 端头压伤 | × | — | × |
| ① 构件存在附加损伤。 ② i表示至少有一个频率变化大于该批构件损伤前的频率偏差;ii同i,但至少有两个模态;iii表示至少有一个频率变化大于重复测量频率的偏差;iv同iii,但至少有两个模态。× 显示可能有损伤;×× 十分肯定有损伤;× 频率增加时指示有损伤。* |
对于飞机上常用的复合材料及胶接结构平板件,检测重点往往在于评估材料的均质性及内部损伤。常用的方法有半功率点带宽法和自由振动衰减法,两者都与测量结构的阻尼特性有关。
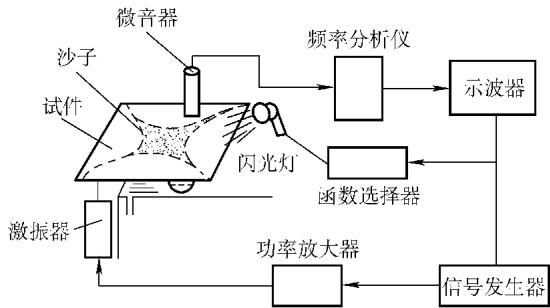
试验考量:
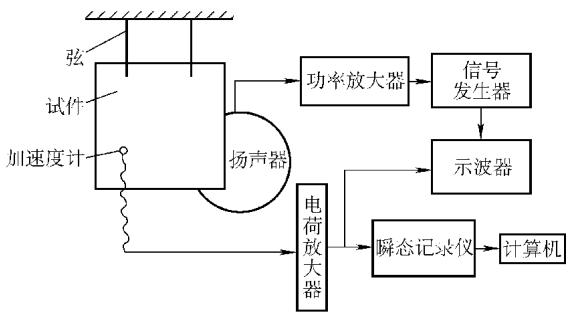
应用实例: 以云母基复合材料板为例,通过对比两块A类板的振型和阻尼,可以发现:尽管两者的自然频率相同,但A-2板的振型明显不对称,且阻尼值更大,这揭示了其内部材料(云母填充料)分布不均的问题。相比之下,A-1板的振型对称、阻尼较小,均质性更好。
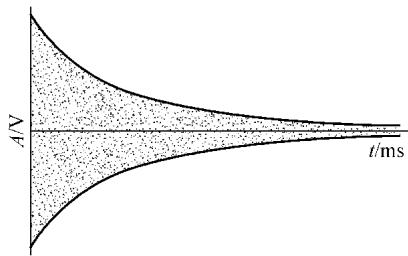
通过对B类方板的自然频率、振型和阻尼值进行综合比较,可以清晰地对三块板的质量进行排序:B-2最好,B-1次之,B-3最差。这些结论与其他无损检测方法的结果高度一致,证明了振动分析在材料均质性评估中的有效性。
要获得一张信噪比高、结果可靠的图谱,对样品制备、设备参数配置、测试环境控制都有极高要求。这正是专业检测实验室的核心价值所在。 精工博研测试技术(河南)有限公司(原郑州三磨所国家磨料磨具质量检验检测中心),央企,国字头检测机构,专业的权威第三方检测机构,专业检测复合材料结构振动模态分析,可靠准确。欢迎沟通交流,电话19939716636
振动分析作为一种无损检测手段,其历史悠久,但真正实现从“特殊”到“普及”的飞跃,则得益于过去数十年微处理器和信号处理技术的惊人发展。如今,它已成为与常规NDT技术并列的重要专业,尤其在旋转机械的状态监测和故障诊断领域,扮演着不可或替代的角色。
它与传统振动学中的“振动测试”有所区别。后者旨在研究样机或模型的动力特性,为改进设计、提升稳定性与舒适性服务。而作为无损检测手段的振动分析,其目标更为直接:通过解读旋转设备发出的振动“信号”,查找并定位其中存在的缺陷与故障。
每一台旋转的机器,都有其独一无二的振动“指纹”——一个由机器设计、制造精度、零件磨损等所有因素综合决定的特征波形。熟悉并监测这个指纹的变化,是实现预测性维护、避免重大事故的关键。
振动的语言——正弦波:最基础的振动(简谐振荡)可以用正弦波来描述:d = Dsin(ωt + φ₀)。其中,振幅(D)、频率(ω)和相位(φ₀)是描述振动的三个核心要素。一台复杂机器的振动,本质上是无数个不同频率、振幅和相位的正弦波的叠加。而快速傅里叶变换(FFT)技术,就是将这个复杂的叠加波“解码”成一系列简单正弦波的强大工具,使我们能够分析每一个振动成分的物理意义。
描述振动的标尺:
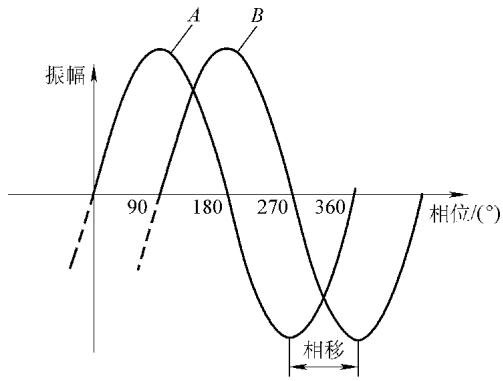
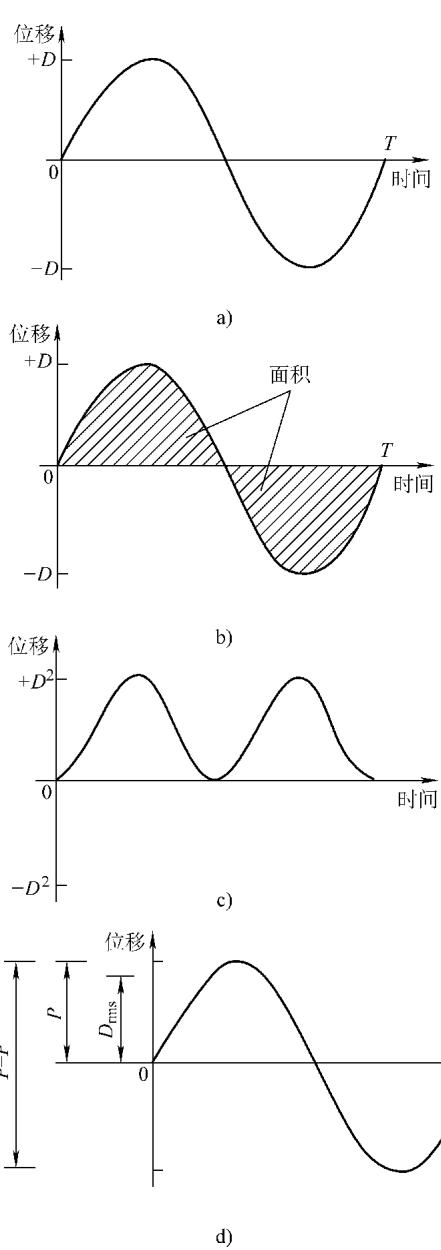
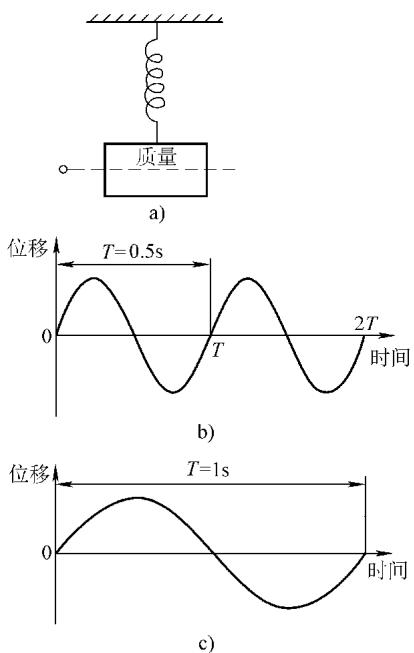
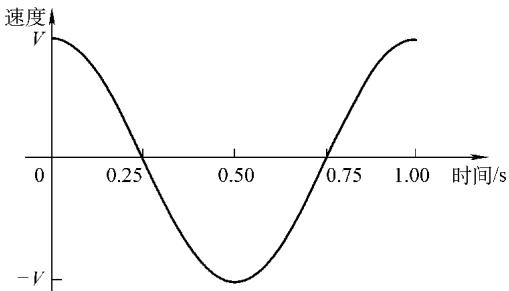
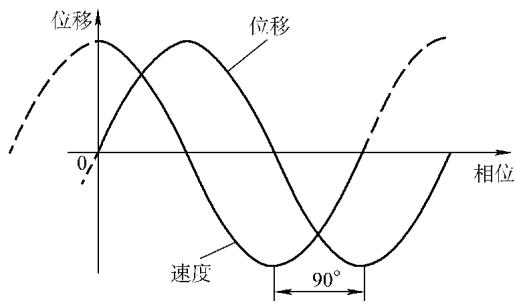
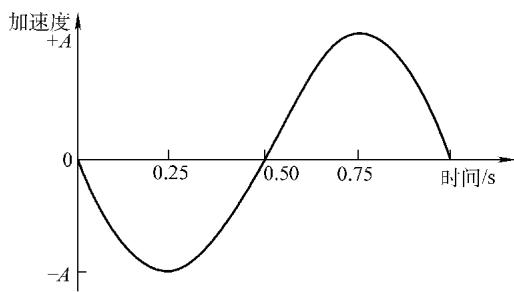
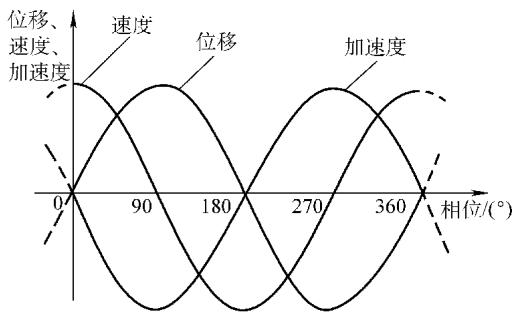
分贝(dB)的应用:由于振动和声强的数量级差异巨大,我们常用对数标度——分贝(dB)来表示。对于振幅等量值,其分贝值 LD = 20lg(D/Dr),其中 Dr 是一个标准基准值。分贝的使用使得我们能在同一尺度下方便地比较和分析宽动态范围的信号。
信号的“滤镜”——滤波器:原始的振动信号是所有振动源的混合体,信息庞杂。要从中提取有用信息(例如,从齿轮啮合噪声中分辨出轴承的磨损信号),就必须使用滤波器。带通滤波器是振动分析仪的核心,它只允许特定频率范围内的信号通过。滤波器的带宽和下降率(衰减锐度)直接决定了分析仪的分辨力和测量精度。
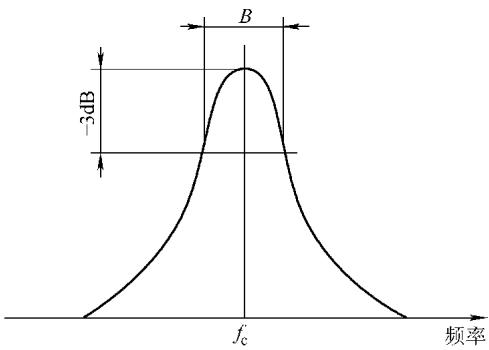
振动分析的实践是一门结合了理论、数据和经验的艺术。从选择测量点到最终的故障诊断,需要一套系统性的逻辑。
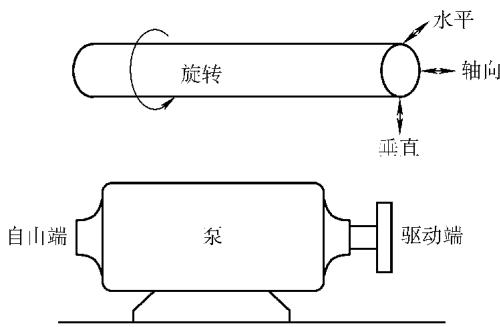
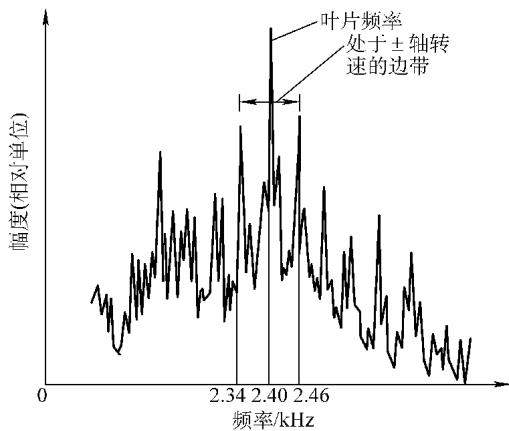
频谱分析是振动诊断的“杀手锏”。通过FFT分析仪得到的频谱图,就像是机械的“心电图”,不同的“波形”对应着不同的健康状况。要读懂这张图,关键在于理解各种“受迫振动频率”的成因。
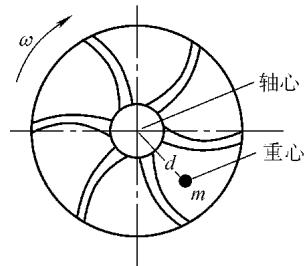

叶片通过频率 (BPF):等于叶片数乘以轴转速。泵、风机、压缩机等叶片机械都会有此特征频率。该频率幅值异常高,可能意味着叶尖与壳体间隙过小或流动失速等问题。
齿轮啮合频率 (GMF):等于齿数乘以其轴转速。GMF处的高幅值通常指示齿形误差、磨损或不合适的齿隙。而GMF两侧的边带则信息量更大:以小齿轮转速为间隔的边带,通常与小齿轮的偏心或安装问题有关;以大齿轮转速为间隔的边带则指向大齿轮。边带越多、能量越高,问题越严重。检查齿轮信号时,常常需要用到频谱的频率扩展(Zoom-FFT)功能,以获得足够的分辨率来区分间隔很近的边带。
滚动轴承频率:轴承的损伤会产生一系列特征频率,分别对应内圈、外圈、滚动体和保持架的缺陷。这些频率可以通过轴承的几何参数和转速精确计算得出:
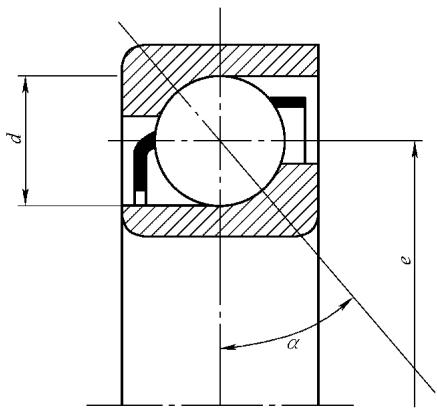
轴承的早期损伤会产生高频的冲击脉冲,这些脉冲会激励加速度计自身的共振频率(通常在30-90kHz),形成所谓的“激振脉冲”,是轴承早期失效的灵敏指标。但这种方法易受其他高频噪声源(如蒸汽泄漏)的干扰。
掌握这些基本机理,再辅以严谨的逻辑推理,振动分析工程师就能像一位经验丰富的医生,通过“听诊”——分析振动频谱,准确诊断出旋转机械内部的各种疑难杂症。
从简单的敲击到复杂的频谱分析,振动检测技术为我们提供了一双能够“看见”结构内部状态的眼睛。然而,要精确解读这些振动信号,不仅需要扎实的理论知识,更需要专业的测试设备和丰富的实践经验。如果您在实际工作中也面临类似的旋转机械故障诊断挑战,我们非常乐意与您一同探讨解决方案。 精工博研测试技术(河南)有限公司(原郑州三磨所国家磨料磨具质量检验检测中心),央企,国字头检测机构,专业的权威第三方检测机构,专业检测旋转机械振动故障诊断,可靠准确。欢迎沟通交流,电话19939716636


 首页
首页
 检测领域
检测领域
 服务项目
服务项目
 咨询报价
咨询报价