声-超声波检测信号处理：从傅里叶变换的局限到小波变换的精髓

在声-超声波无损检测领域，我们面对的并非干净、规整的信号，而是一幅幅充满挑战的复杂图景。当探询的应力波穿透工件，与内部的微结构和不连续性相互作用后，我们接收到的信号便被深刻地“调制”了。这种信号与我们熟悉的声发射信号在本质上极为相似，其处理与解读的水平，直接决定了检测的成败。

一、 解码声-超声波信号的“天性”

要有效处理声-超声波信号，首先必须理解其固有的复杂特性。它并非简单的周期波，而是多种物理现象交织的产物。

• 多频率与宽频带：激发信号本身是高频、高阻尼的窄脉冲冲击波，其持续时间极短。然而，一旦与材料内部结构作用，后续产生的信号便在频域上极度丰富，展现出宽广的频谱特征。
• 随机性与不确定性：信号的形态被材料内部微观世界的不连续性（如微裂纹、夹杂、孔隙）随机调制。这意味着我们无法预知信号的具体波形，其时域和频域的统计特性都随时间动态变化，是典型的非平稳随机信号。
• 波形多样性：声-超声波在介质中传播时，会经历反射、折射、波形转换等一系列复杂过程。这使得最终接收到的信号，其波形模式远比初始的探询波复杂。有趣的是，这种在声发射检测中常被视为干扰的传播效应，在声-超声波技术中却可能携带了可供分析的宝贵信息。
• 普遍存在的干扰噪声：在真实的工业环境中，电源噪声、仪器电子噪声、电磁干扰以及环境噪声无处不在。这些噪声通常随机分布在整个采样时间内，进一步掩盖了我们真正关心的缺陷信号。

面对如此复杂、多变且充满噪声的非平稳信号，传统的分析工具是否还能胜任？

二、 传统分析方法的“窘境”：为何傅里叶变换力不从心？

长期以来，傅里叶变换是信号分析的基石。然而，它在处理声-超声波这类信号时却显得力不从心。

经典的傅里叶变换是一种全局分析方法，它能告诉我们信号中包含了哪些频率成分，但完全丢失了这些频率成分出现的时间信息。这对于分析瞬态、突变的信号是致命的。

为了解决这个问题，短时傅里叶变换（STFT）应运而生。它通过一个固定宽度的“窗函数”来截取信号片段进行分析，试图同时获得时间和频率信息。但其根本缺陷在于“单分辨率”——窗的宽度一旦固定，时间分辨率和频率分辨率就成了相互制约的死对头。对于信号中变化剧烈的高频部分（如裂纹尖端的突变），我们需要极高的时间分辨率（窄窗）；而对于变化平缓的低频部分，我们又需要极高的频率分辨率（宽窗）。STFT的固定窗宽无法同时满足这两个要求，因此很难获得理想的分析效果。

那么，是否存在一种工具，能像变焦镜头一样，智能地调整其分辨率，从而完美地解析这类非平稳信号呢？

三、 小波变换：为非平稳信号分析而生的“数学显微镜”

小波变换（Wavelet Transform）正是为解决这一难题而生的。它是一种先进的时频分析方法，其核心优势在于多分辨率特性。

小波变换能够在时域和频域同时表征信号的局部特征，它能做到：

• 在信号的高频区（对应细节、突变），提供高时间分辨率和低频率分辨率。
• 在信号的低频区（对应概貌、缓变），提供高频率分辨率和低时间分辨率。

这种特性使其天然适合分析声-超声波检测中那些瞬态的、异常变化的信号成分。自20世纪90年代被引入无损检测领域以来，小波变换已从语音分析等成熟领域，成功拓展至超声、声发射及声-超声波检测中，并由国内高校和研究机构推动，取得了丰硕的研究成果。

1. 小波变换的物理概念与算法

小波变换的分析过程，可以直观地理解为：用一个被称为“母小波”或“基本小波” ψ(t) 的函数，通过伸缩和平移，去匹配信号的各个部分。

设一个待分析信号为 f(t)，它是一个平方可积函数，记为 f(t) ∈ L²(R)。母小波 ψ(t) 及其傅里叶变换 ψ'(ω) 都是带限函数。通过对母小波进行伸缩和平移，可以得到一个小波基函数族 ψ_a,b(t)。

其在时间域的窗口由下式定义： [b + at* - aΔψ, b + at* + aΔψ]

其在频率域的窗口则为： [ω*/a - Δψ'/a, ω*/a + Δψ'/a]

这里的 a 是尺度因子，b 是平移因子。

• 平移因子 b 控制着小波窗口在时间轴上的移动，实现对信号的逐点扫描。
• 尺度因子 a 控制着小波的“胖瘦”。a 越大，小波在时域上越宽，对应频域上越窄，用于分析信号的低频成分；a 越小，小波在时域上越窄，对应频域上越宽，用于分析信号的高频成分。

因此，小波变换就像一个可调节带宽的滤波器组，在不同频率范围内对信号进行精细剖析。

信号 f(t) 的连续小波变换定义为： Wf(a,b) = (1/√a) ∫ f(t)ψ((t - b)/a)dt

其逆变换可以将信号重构回来： f(t) = (1/Cψ) ∫∫ Wf(a,b)ψ((t - b)/a)dadt 其中 Cψ 是一个允许条件常数，确保变换的可逆性。

母小波 ψ(t) 的选择并非唯一，只要满足允许条件即可。工程应用中常用的小波基包括：Hear小波、Morlet小波、Mexican Hat小波、Daubechies小波系、Coiflets小波系等。选择不同的小波基分析同一信号，可能会得到不同的结果，因此小波基的选择至关重要。

2. 从连续到离散：二进制小波变换

在计算机上实现连续小波变换需要巨大的计算量。为了提高效率，通常采用离散小波变换，特别是将尺度因子 a 按2的幂级数进行离散化，即 a₀ = 2。这样得到的离散小波基函数为： ψ_j,k(t) = 2⁻ʲ/²ψ(2⁻ʲt - kτ) 其中 τ 是采样周期。

这种二进制小波变换只对尺度因子 a 离散化，而时间平移因子 b 仍然保持连续变化。这一特性赋予了它强大的“变焦距”功能，既能深入信号的细节，又不破坏其在时域上的连续性，完美契合了声-超声波信号分析的需求。要准确地应用这些复杂的数学工具并从海量数据中提取可靠的缺陷信息，需要深厚的理论知识和丰富的实践经验。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测复合材料缺陷分析，可靠准确。欢迎沟通交流，电话19939716636

四、 应用实例：小波变换在蜂窝结构脱胶检测中的威力

理论的价值最终要在实践中体现。清华大学张平博士在其研究项目中，就成功运用小波变换对蜂窝结构材料的声-超声波检测信号进行了特征分析，准确地识别了材料内部的脱胶缺陷。

研究中，对包含完好区域、Φ20mm和Φ40mm人工脱胶缺陷的三种蜂窝结构试件进行声-超声波检测。获得的三种信号时域波形如下图所示。

图1 蜂窝结构材料声-超声波检测信号

从图1可以看出，仅凭肉眼观察时域波形，几乎无法区分这三种状态。

研究人员利用小波变换对信号进行分解，发现在D2和D3这两个分解尺度上，包含了信号前端近似指数衰减的特征分量。这两个尺度因此被确定为该检测信号的特征频带。

随后，对这个特征频带内的信号进行重构，并分析其小波分解系数的能量特征。结果如图2的直方图所示。

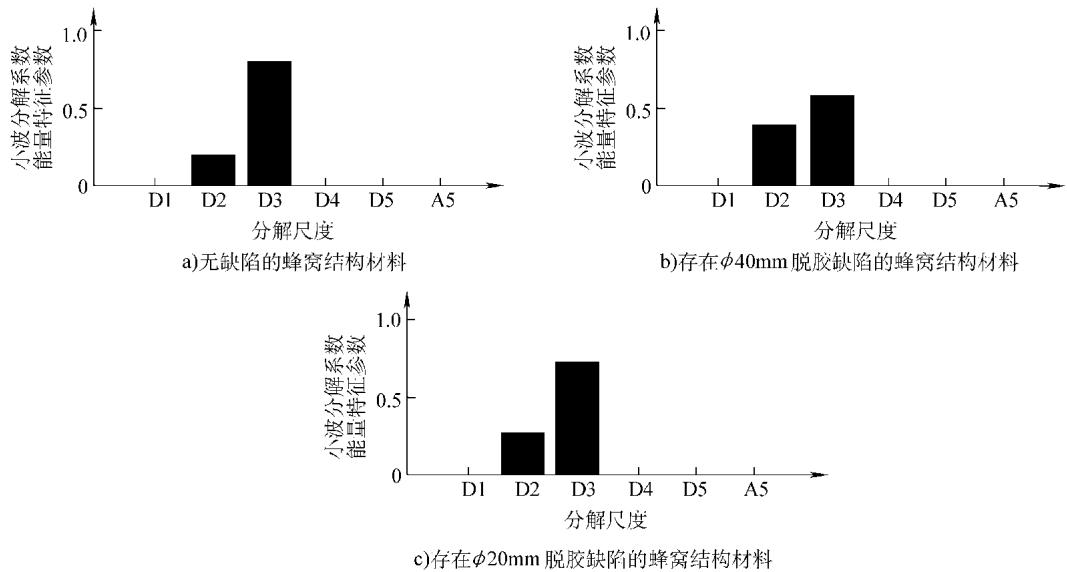
图2 蜂窝结构材料声-超声波检测信号的小波分解系数能量特征分布

图2清晰地揭示了规律：

1. 信号能量主要分布在D2和D3尺度。
2. 存在脱胶缺陷的信号，其能量更多地分布在高频的D2尺度上。
3. 随着脱胶缺陷面积的增大（从Φ20mm到Φ40mm），D2尺度上的能量也随之增大。

这一现象背后的物理机制是：当应力波传播至脱胶区域时，相当于在厚度很小的面板中传播，这会激发高频驻波的产生。小波分解的能量特征参数成功地捕捉到了这一由缺陷引起的细微变化，将隐藏在复杂波形中的缺陷信息清晰地呈现出来。

这个案例有力地证明，小波变换不仅是一种强大的数学工具，更是连接复杂信号与材料内部物理状态的桥梁，为高要求的无损检测与质量控制提供了深刻的洞见。