可靠性的统计学处理方法

可靠性，作为一个统计学量，其描述与分析离不开相应的统计工具。本文旨在探讨描述时变失效行为的几个核心可靠性函数与参数，并深入分析作为统计离散性根源的应力-强度干涉模型。

可靠性函数

对于一个给定的时间点 t，失效概率函数 F(t) 描述了设备在 0 到 t 这个时间区间内发生失效的概率。

为了定量描述，我们引入设备寿命 L 的概念。L 的单位可以是时间、循环次数或任何与设备生命周期相关的量。于是，失效概率 F(t) 被定义为寿命 L 小于或等于观测时间 t 的概率 P：

$$ F(t) = P(L /leq t) $$

F(t) 也可以写作其失效密度函数 f(t) 的积分形式：

$$ F(t) = /int_{0}^{t} f(t’) dt’ $$

失效密度函数 f(t) 具有很强的实际意义，因为许多概率分布通常是以密度函数的形式给出的。一个典型的例子就是我们熟知的钟形曲线，它是高斯正态分布的密度函数，而非分布函数本身。

有了失效概率，其补集——生存概率，也就能顺理成章地得到。这个生存概率 R(t) 被称为可靠度函数，或简称为可靠度：

$$ R(t) = 1 - F(t) = 1 - P(L /leq t) = P(L > t) $$

而我们之前定性提及的失效率，现在可以被精确地定义为 λ(t)：

$$ λ(t) = /frac{f(t)}{R(t)} $$

λ(t) 描述的是设备在已经成功运行到时间 t 的条件下，在下一个瞬间 t + dt 内发生失效的概率。

图1 示意性地展示了这四个核心函数之间的关系。

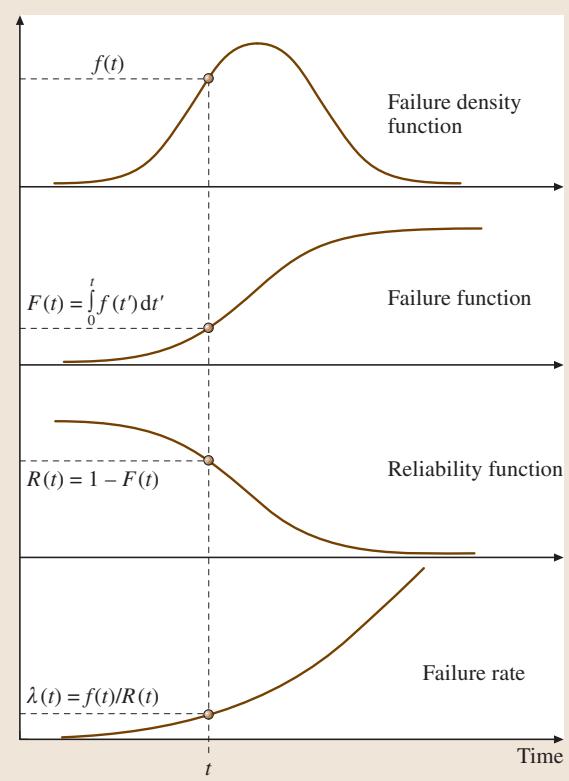图1 四个相关可靠性函数的示意图，特别展示了失效密度函数与其他函数间的关系

寿命参数

在工程实践中，可靠性分析需要回答一系列关于设备寿命的问题。针对问题的性质，不同的寿命参数便有了用武之地。

平均寿命

平均寿命，在针对不可修复系统的文献中常被称为平均无故障时间（MTTF），是可靠度函数 R(t) 的期望值。根据统计学理论，期望值可以通过对密度函数积分计算得出：

$$ /mathrm{MTTF} = E(L) = /int_{0}^{/infty} tf(t)dt = /int_{0}^{/infty} R(t)dt $$

在许多教材和手册中，MTTF 被用作比较不同设备失效行为的特征指标。由于MTTF可以从一个给定的 f(t) 计算出来，且与具体的失效模式无关，它成为了一个通用的寿命表征量。

然而从实践角度看，在很多情况下计算MTTF并不方便，原因有二：

• 上述积分可能没有解析解。
• 当失效遵循一个明确的统计模型时（如威布尔分布、对数正态分布、指数分布等），这些模型自身带有更易于计算且与模型直接关联的寿命特征值，而这些特征值通常与MTTF并不等同。例如，威布尔模型使用的便是其特有的特征寿命。

B_γ 寿命，即 γ% 百分位数寿命

B_γ 寿命是指产品失效概率达到 γ%（即所谓的 γ% 百分位数）时所经历的寿命。简单来说，B₁₀ 寿命就是指有 10% 的设备发生失效的时刻点。其精确定义为：

$$ F(B_{/gamma}) = /gamma /% /quad /text{或} /quad B_{/gamma} = F^{-1}(/gamma /%) $$

B₁₀ 寿命（以及更低的百分位数寿命，如 B₁、B_0.1、B_0.001）在可靠性工程中具有举足轻重的地位。它允许工程师在对大多数产品至关重要的可靠性区间（即失效概率 F < 10%，可靠度 R > 90%）内对设备的可靠性进行直接比较。

其他寿命参数

此外，还有一些其他的寿命参数，如中位寿命和众数寿命。但这些参数或多或少偏向理论性质，在日常实践中很少使用。为了知识的完整性，我们在此给出它们的定义。

• 中位寿命 L<sub>Median</sub>：定义为失效概率达到 50% 时的寿命。根据 B_γ 寿命的定义，它等同于 B₅₀ 寿命。 $$ F(L_{/mathrm{Median}}) = /int_{0}^{L_{/mathrm{Median}}} f(t)dt = 50/% $$
• 众数寿命 L<sub>Modal</sub>：定义为失效最集中的时刻，等同于失效密度函数 f(t) 的峰值点。 $$ /mathrm{d}f(L_{/mathrm{Modal}}) / /mathrm{d}t = 0 $$

应力-强度干涉模型

失效概率的时间依赖性，其根源在于外部施加的应力（Stress）的统计离散性与材料自身宏观强度（Strength）的统计离散性之间的相互作用。这里的“应力”泛指作用于设备的任何物理过程，如机械应力、电压、温度或湿度；而“强度”则是指设备抵抗这些应力的能力。两者具有相同的物理量纲，在此统一用 σ 表示。

图2 (a) 静态与 (b) 动态干涉模型。设备失效概率取决于应力与强度分布密度曲线下的重叠区域。

强度 σ<sub>S</sub> 的离散性源于制造工艺和材料性能的波动。应力 σ<sub>L</sub> 的离散性则来自不同的用户和变化的使用环境。

一旦应力超过强度，失效便会发生。因此，失效概率取决于随机抽取的应力条件超过随机选取的设备强度的可能性。这一概率取决于两者分布函数的重叠区域，如图2(a)所示的静态应力-强度干涉模型。

该重叠区域的面积，即失效概率 F，可计算如下：

$$ F = P(/sigma_{/mathrm{L}} > /sigma_{/mathrm{S}}) = /int_{-/infty}^{/infty} f_{/mathrm{L}}(/sigma) /left[ /int_{-/infty}^{/sigma} f_{/mathrm{S}}(/sigma) d/sigma /right] d/sigma $$

其中 f<sub>L</sub> 和 f<sub>S</sub> 分别是应力和强度的密度函数。

同样的逻辑也适用于动态干涉模型（图2(b)）。在 t = 0 时，由于两个分布函数的重叠可以忽略不计，失效概率为零。但随着服役时间的推移，材料内部的微观结构发生变化，导致强度的平均值下降。此时，F 随着运行时间的增加而显著增大。

应力-强度干涉模型的一大优点在于，它为时变失效概率的起源提供了一个非常直观且合理的物理解释。然而，它并不适合用于定量地确定设备的可靠性。究其原因，是该模型的应用要求我们精确掌握应力和强度分布函数在“尾部”区域的准确形态，而这一要求在实际工程中通常难以满足。要准确获取这些极端条件下的数据，需要大量的实验和精密的分析。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测可靠性测试与寿命评估，可靠准确。欢迎沟通交流，电话19939716636