威布尔分析：从失效数据到可靠性洞见的实践指南

在可靠性工程领域，核心任务之一便是对各类失效数据进行深度剖析。这些数据可能源于实验室的可靠性测试，也可能来自对现场产品保修数据的分析。在众多分析工具中，威布尔分析（Weibull analysis）凭借其强大的灵活性和广泛的适用性，已成为现代工业界处理寿命数据的主流方法。尽管在某些特定场景，如材料的疲劳强度和性能退化现象中，对数正态分布（lognormal distribution）也扮演着重要角色，但威布尔分布的通用性使其地位难以撼动。

威布尔分布函数的核心思想

威布尔分布之所以备受青睐，在于其是一个多用途的分布模型。通过调整其参数，它几乎可以模拟任何一种实际的失效行为模式。其核心由两个函数定义：失效概率函数 F(t) 和失效密度函数 f(t)。

失效概率函数 F(t)，表示产品在时间 t 之前发生失效的累积概率： F(t) = 1 - e^-(t/η)β

失效密度函数 f(t)，表示产品在时间点 t 发生失效的瞬时概率： f(t) = (β/η) * (t/η)^β-1 * e^-(t/η)β

相应地，可靠度函数 R(t)，即产品在时间 t 仍然正常工作的概率，为 R(t) = 1 - F(t)： R(t) = e^-(t/η)β

这些公式的核心在于两个关键参数：

• 形状参数 β (beta)：也称威布尔斜率，它决定了失效率随时间变化的趋势，是揭示失效物理机制的窗口。
• 特征寿命 η (eta)：当 t = η 时，失效概率 F(t) 恒等于63.2%。它代表了产品失效分布的一个关键时间点。

形状参数 β 的值至关重要，它直接关联到著名的“浴盆曲线”的三个阶段，从而帮助我们判断产品处于哪个生命周期阶段：

• β < 1：对应浴盆曲线的早期失效区（婴幼儿期）。此时失效率随时间递减，表明早期缺陷（如制造瑕疵）正被逐渐淘汰。
• β = 1：对应浴盆曲线的偶然失效区（稳定期）。此时失效率为常数，与时间无关，表明失效是随机发生的。这种情况下，威布尔分布退化为指数分布，具有“无记忆性”的特点。电子元器件的失效行为常常符合这一模式。
• β > 1：对应浴盆曲线的耗损失效区（老年期）。此时失效率随时间递增，表明产品因磨损、老化、疲劳等原因进入了寿命末期。当 β 约等于3.5时，其分布形态近似于高斯分布（正态分布）的钟形曲线。

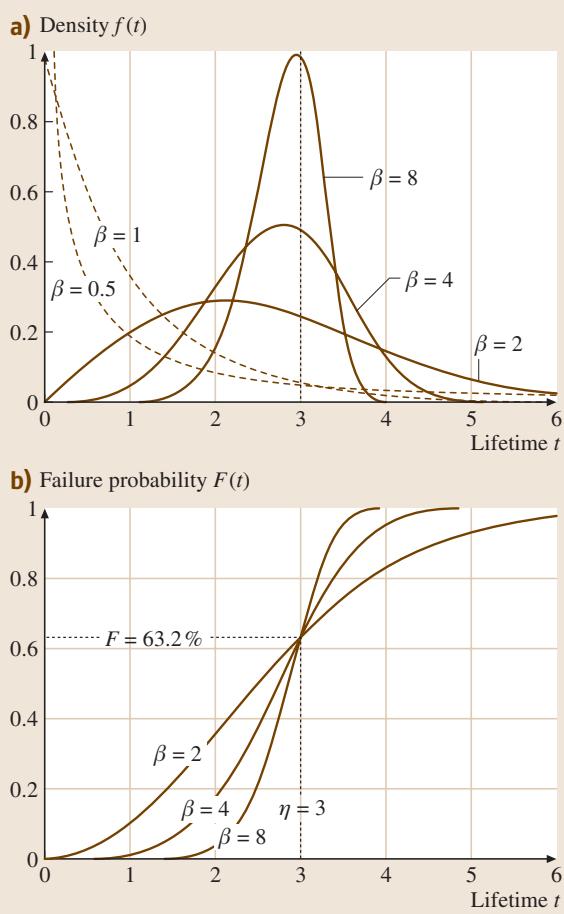图1. 不同形状参数β下威布尔分布的(a)密度函数与(b)失效概率图 (η=3)

从图1的密度函数图中可以看出，只有当 β > 1 时，曲线才呈现出明显的峰值（钟形）。而当 β < 1 时，曲线单调递减，没有局部极值。从失效概率图中则可以观察到一个有趣的现象：特征寿命 η 的值（对应失效概率63.2%的时间点）与 β 无关。

威布尔分析实战：中位秩回归法 (MRR)

理论的价值在于应用。那么，我们如何从一堆散乱的失效数据中，提炼出这些关键参数呢？常用的方法有两种：中位秩回归法（Median Rank Regression, MRR）和最大似然估计法（Maximum-Likelihood Estimation, MLE）。后者是一种需要大量计算的数值方法，而前者则更为直观，在工程实践中广为流传。因此，我们聚焦于MRR方法的具体操作。

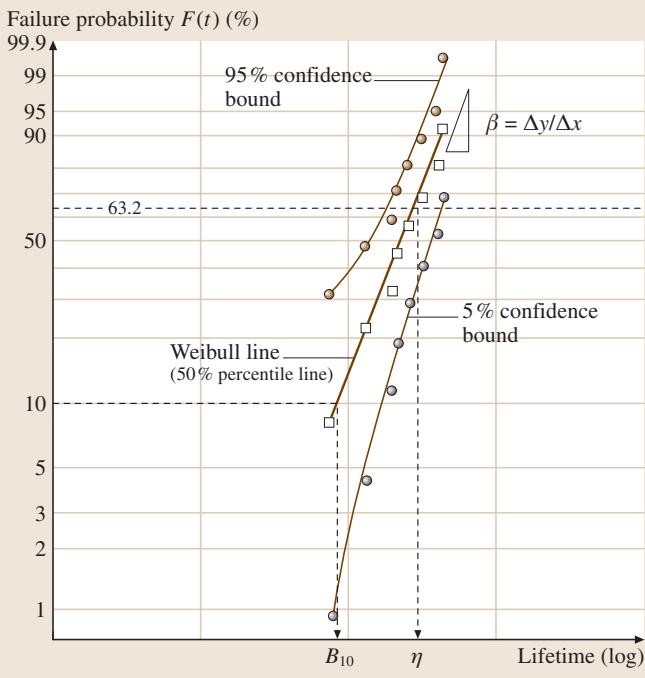图2. 威布尔概率图示意图。方形数据点代表实测寿命及对应的中位秩F(L_i)，深色圆点代表5%和95%置信界限。β值由回归线的斜率估算，特征寿命η由回归线与63.2%概率线的交点确定。B₁₀寿命则定义为失效概率F=10%时的寿命值。

MRR分析流程可分解为以下几个步骤：

1. 数据收集与排序 对 n 个样品进行寿命测试，得到 n 个寿命数据 L₁, L₂, …, L_n。将这些寿命值按从小到大的顺序排列，如表1所示。

表1. 实测寿命数据L_i、中位秩失效概率F_50%(L_i)及用于计算置信区间的F_5%和F_95%百分位数

2. 中位秩计算 这是MRR方法的核心。我们只有寿命数据 L_i，却缺少其对应的失效概率 F(L_i)。这个概率无法直接通过实验测得，必须借助统计理论进行估算。其背后的推导涉及二项分布，过程较为复杂，但对于应用者而言，掌握其近似计算公式即可。一个广为接受且常用的公式是Benard提出的中位秩近似公式：

F_50%(L_i) ≈ (i - 0.3) / (n + 0.4)

这里的下标 50% 指的是失效概率分布的中位数，切勿与寿命分布的中位数混淆。这些值也可以通过查阅标准的中位秩表得到。

3. 概率绘图与线性化 将计算出的失效概率 F(L_i) 与对应的寿命 L_i 绘制在特殊的“威布尔概率纸”上。如果这批数据确实服从威布尔分布，那么这些数据点将近似排列成一条直线。这一步的精髓在于坐标变换，通过对失效概率函数 F(t) 进行两次对数变换，可以将其转化为一个线性方程：

ln{-ln[1 - F(L_i)]} = β * ln(L_i) - β * ln(η)

这个方程完美地符合了线性方程 y = Ax + B 的形式，其中： y_i = ln{-ln[1 - F(L_i)]} x_i = ln(L_i) A = β B = -β * ln(η)

通过这种方式，复杂的非线性问题被巧妙地转化为了直观的线性回归问题。

4. 参数求解与拟合优度评估 一旦数据被线性化，就可以通过标准的线性回归方法计算出斜率 A 和截距 B。进而，威布尔参数便可轻松求得：

β = A η = exp(-B / β)

同时，我们还需要评估数据点与回归直线的拟合程度。常用的指标是相关系数 (CC)，其值介于0和1之间，越接近1，表明线性关系越好，数据服从威布尔分布的假设也越可靠。

5. 引入置信区间 由于我们的分析是基于有限的样本，得到的结果必然存在不确定性。置信区间 α 是一个衡量分析结果可信度的重要参数。例如，设定90%的置信区间，意味着我们有90%的把握认为真实的威布尔回归线落在我们计算出的置信界限之内（通常由5%和95%两条线构成）。

一个常见的误区是认为置信区间的宽度与数据的离散程度有关。实际上，其宽度仅取决于样本量 n。样本量越大，统计论证的力度越强，置信区间就越窄，分析结果也就越精确。当样本量大于50时，置信区间的影响在许多情况下可以忽略不计。

整个过程虽然步骤清晰，但涉及大量的数据处理和统计判断，尤其在置信区间的解读和拟合优度评估上，极易出现偏差，从而影响最终决策的准确性。这正是专业检测实验室的核心价值所在。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测材料寿命与可靠性分析，可靠准确。欢迎沟通交流，电话19939716636

进阶应用：三参数威布尔分析

在某些情况下，二参数模型不足以精确描述失效行为，特别是当产品存在一个明确的“无失效”初始阶段时。这时，就需要引入第三个参数——失效起始时间 t₀。

三参数威布尔失效概率函数变为： F(t) = 1 - e^{-((t - t₀)/(η - t₀))β}

参数 t₀ 用于描述在退化或磨损实验中常见的“孕育期”，即在时间 t₀ 之前，不会有任何失效发生。引入 t₀ 需要满足一些条件，例如：有足够多的失效样本（有专家建议至少21个甚至100个以上）、失效物理机制支持存在一个无失效区、二参数威布尔图呈现明显的下凹曲线等。

t₀ 的估算可以通过图解法或迭代法完成。一种常用的图解法是Dubey提出的方法，通过在威布尔图上取特定点来估算初始值。更精确的方法是通过试错迭代，不断调整 t₀ 的值，对寿命数据进行变换 (t’ = t - t₀)，然后重新进行二参数威布尔分析，直到找到能使数据点线性度最好（即相关系数CC最大）的 t₀ 值。

实践中的决策：一个材料对比的例子

威布尔分析的最终目的是指导工程决策。假设我们需要为某安全关键部件选择材料，该部件承受变化的机械载荷。实验室对两种材料A和B进行了测试，并进行了威布尔分析。

• 材料A：特征寿命 η_A 较长。
• 材料B：特征寿命 η_B 较短。

仅从特征寿命看，材料A似乎更优。然而，分析同时发现，材料A的威布尔图线更平缓，意味着其形状参数 β_A 较小，数据离散度更大。

对于安全关键部件，我们更关心的是早期失效概率，即低百分位数下的寿命，例如 B₁₀ 寿命（10%的产品发生失效时的时间）。由于材料A的失效分布更分散，其失效曲线在早期（低失效概率区域）会更早地开始，导致其 B₁₀ 寿命反而低于材料B。

这个例子揭示了两个重要的工程智慧：

1. 在实际应用中，尤其是对于高可靠性要求的场合，比较材料或产品优劣应使用 B₁₀ 或更低百分位数的寿命，而非仅仅比较特征寿命 η。
2. 数据离散度大（即形状参数 β 值小）通常比特征寿命略低更为致命，因为它直接关系到产品的早期可靠性。一个性能稳定、表现一致的产品，远比一个平均寿命虽长但早期失效风险高的产品更有价值。