在现代材料科学与工程领域,动态法已成为测定各类材料弹性常数(如杨氏模量、剪切模量)的主流技术。这些方法诞生于20世纪30年代,其核心优势在于测试过程中施加的应力极小,远低于材料的弹性极限。这使得测量能够精准地反映材料的本征弹性,有效规避了静态测试中常见的蠕变或弹性滞后等复杂效应。
由于应力微小,测试过程对样品本身不构成任何损伤,因此可以对同一枚样品进行反复测量。这一特性使得研究人员能够利用单一样品,系统地探究弹性模量随温度、压力等外界条件变化的规律。相较于静态测试所需的大尺寸、复杂形貌的试样,动态法所用的试样通常小巧且简单。
动态测试中,主要包含两大类常用技术。其中之一便是超声脉冲法。其基本原理是向试样中发射一束超声波脉冲,并精确测量其在样品中传播的“飞行时间”(Time of Flight)。通过这种方法测得的弹性常数类型,取决于所用脉冲波的振动模式。
若采用纵波脉冲,其传播速度(v_l)与材料密度(ρ)可直接用于计算杨氏模量(E):
E = ρv_l²
脉冲的传播速度通过测量其在样品内穿过一固定距离所需的时间来直接获得。当采用脉冲回波技术时,对于一个厚度为 L 的样品,波的传播距离通常按 2L 计算。
若换用剪切波脉冲,则可根据其传播速度(v_s)和材料密度(ρ)计算出剪切模量(μ):
μ = ρv_s²
此项技术的测量精度受到诸多因素影响,包括试样的尺寸精度、端面平行度、探头与试样的耦合方式以及信号的信噪比。在理想条件下,其测量精度通常可达平均值的±0.1%。尽管该方法兼具高精度与操作简便的优点,但在材料测试领域并未得到全面的普及。不过,它依然被特定标准所采纳,例如 ASTM C1419-99a 标准就利用该方法在室温下对耐火材料的声速进行测量,并以此估算其杨氏模量。
另一大类动态测试技术是自由振动法,它通过分析杆状试样的自由振动特性来确定弹性常数。试样可以是矩形或圆形截面。通过机械方式(如瞬时冲击或持续驱动)激发试样振动,然后测量其共振频率,结合试样的密度(ρ)或质量(m)以及几何尺寸,即可计算出相应的弹性常数。通过设计不同的激励方式,可以有选择地侧重于测量杨氏模量或剪切模量。
这些计算公式的推导过程,尤其是涉及弯曲振动驻波的方程,相当复杂,在此不作赘述。Tefft的文章对此有详尽的讨论。目前,脉冲激励法和连续共振法均已被多个ASTM委员会采纳为测量弹性常数的标准方法(见表1),且各委员会提出的技术方案彼此高度相似。
表1:采用共振技术测定弹性常数的ASTM标准测试方法
| 标准号 | 标准标题 |
|---|---|
| ASTM C 215 | 混凝土试样基本横向、纵向和扭转频率的测试方法 |
| ASTM C 623 | 用共振法测定玻璃和微晶玻璃的杨氏模量、剪切模量和泊松比 |
| ASTM C 747-93(1998) | 用声共振法测定碳和石墨材料的弹性模量和基频 |
| ASTM C 848-88(1999) | 用共振法测定陶瓷白瓷的杨氏模量、剪切模量和泊松比 |
| ASTM C 885-87(2002) | 用声共振法测定耐火材料形状的杨氏模量 |
| ASTM C 1198-01 | 用声共振法测定先进陶瓷的动态杨氏模量、剪切模量和泊松比 |
| ASTM E 1875 | 用声共振法测定动态杨氏模量、剪切模量和泊松比 |
| ASTM E 1876-01 | 用脉冲激励振动法测定动态杨氏模量、剪切模量和泊松比 |
ASTM E 1876-01 标准对该技术有完整描述。简而言之,其测试装置示意图如图1所示。为简化计算,试样的长度与其最小横截面尺寸之比建议控制在20-25之间。对于矩形棒材的剪切模量测量,推荐其宽厚比大于等于5。试样的支撑点应位于基频振动的节点处,即距两端0.224L的位置。
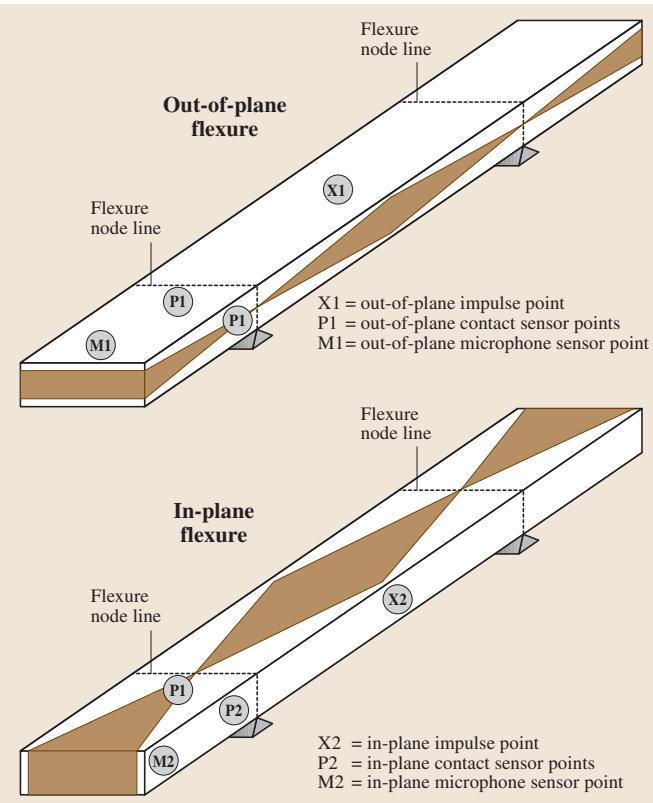
图1 采用自由共振法(弯曲测试)测量弹性模量的试样示意图,依据ASTM E 1876-01标准。
接着,使用一个小型冲击器(如图2所示)敲击试样,激发其振动。振动信号由位于振动腹点(振幅最大处)的麦克风传感器拾取。或者,也可以使用靠近节点线的接触式传感器来采集信号。图1清晰地标示了冲击点和传感器的建议位置。
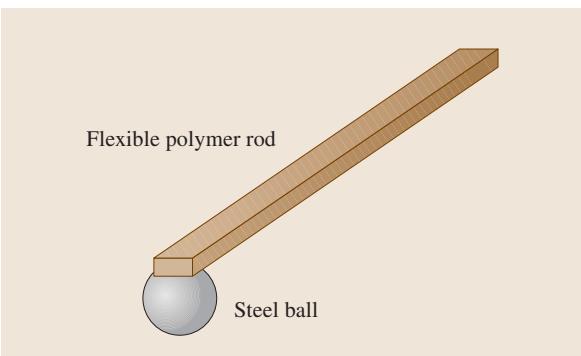
图2 用于小型试样的典型冲击器,依据ASTM E 1876-01标准。
杨氏模量(E)通过以下公式计算,其中涉及基频振动频率(f_f)、试样质量(m)、宽度(b)、长度(L)、厚度(t)以及一个修正因子(T_1):
E = 0.9465(mf_f²/b)(L³/t³)T_1
该修正因子是一个复杂的代数项,与泊松比、试样的厚度和长度有关。当试样长度达到厚度的20倍以上时,可以很好地近似认为T_1与泊松比无关。在此极限条件下,T_1可简化为:
T_1 = 1.000 + 6.585(t/L)²
对于圆形截面试样,测定杨氏模量的流程与矩形试样相似,但计算公式有所不同,具体可查阅ASTM E 1876标准。此外,杨氏模量也可以通过对矩形试样施加纵向振动来获得,即在一端冲击,在另一端拾取振动信号。相关的计算公式和详细步骤同样在ASTM E 1876中有规定。
动态剪切模量(G)的测定可采用与杨氏模量测量时几何形状相似的矩形试样。与弯曲测试一样,试样支撑点也位于节点线上,但其位置与弯曲测试的节点线显著不同(如图3所示)。图3展示了扭转测试中支撑线、冲击点和传感器的位置。一旦测得基频扭转共振频率(f_t),即可通过下式计算动态剪切模量:
G = (4Lmf_t² / bt) [B / (1 + A)]
其中,B和A是修正因子,其具体表达式可在ASTM E 1876中找到。
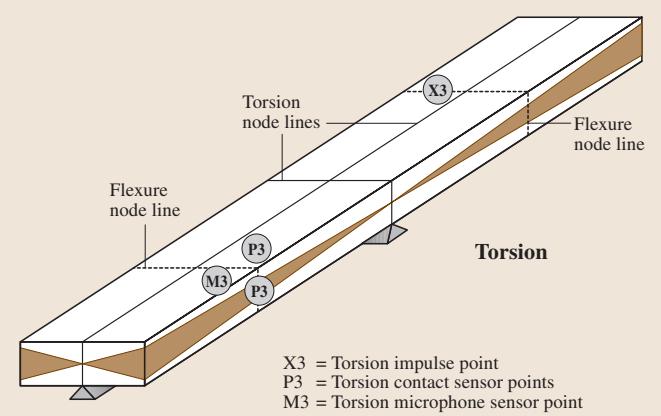
图3 采用自由共振法(扭转测试)测量弹性模量的试样示意图,依据ASTM E 1876-01标准。
连续共振法与脉冲激励法的区别仅在于激发共振的方式不同,因此,用于计算剪切模量和杨氏模量的公式是完全相同的。图4展示了一种典型的测试配置。矩形试样由两根细线或金属丝悬挂。激励换能器通过其中一根悬线向试样传递声波振动,而信号则通过另一根悬线上的探测器接收。通过扫描输入信号的频率,当信号强度出现显著增强时,即表明达到了共振频率。
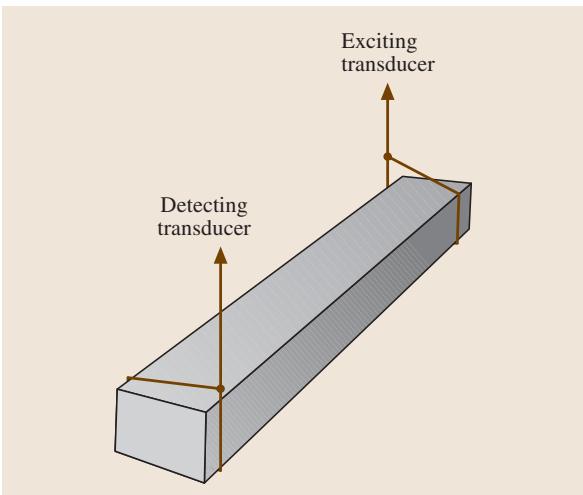
图4 采用连续共振技术测定弹性模量的实验装置示意图,依据ASTM E 1875标准。
操作中的一个关键挑战是必须仔细区分弯曲共振模态、扭转共振模态以及它们各自的谐波。ASTM E 1875标准对此提供了实现方法建议。图5展示了另一种支撑配置,将支撑点直接置于共振节点下方,这种方式有助于优先激发相应模态的基频谐波。尽管如此,要精确识别共振频率,仍需沿着试样全长移动换能器来确定节点和腹点的位置。悬挂法已被成功应用于测定材料从深冷到高温范围内的弹性模量。
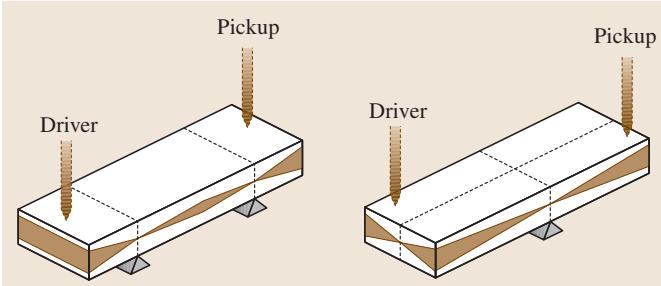
图5 采用连续共振技术的另一种配置,支撑点直接位于共振节点下方,依据ASTM E 1875标准。
从历史发展来看,静态法是最早被开发出来的弹性常数测量方法。动态法则直到20世纪30年代才出现,并经历了一段时间才广为人知并流行起来。静态法的相关标准,如ASTM E 111,于20世纪50年代制定(首版于1955年)。相比之下,动态技术的发展依赖于复杂的理论分析和数值计算,以建立共振频率与试样形状、密度及尺寸之间的关系。同时,现代电子技术的发展也是实现精确共振频率测量的先决条件。直到20世纪50年代末,相关技术取得足够进展,动态法才变得易于使用且实用。第一个关于共振法测量弹性常数的ASTM标准(C 623)在1969年发布,距离该技术成型大约过去了10年。
早在1935年,Ide就认识到动态法相比静态法的优越性。他指出:“动态法测量杨氏模量比常规静态法更具优势。动态模量是在远低于弹性极限的微小交变应力下获得的,不会引发复杂的‘蠕变’效应或弹性滞后。这精确地满足了数学理论的假设。” 这种关于动态法固有优越性的观点至今仍被广泛认同。
在一项由Smith等人进行的研究中,研究人员使用动态测试技术测定一种因科镍(Inconel)合金的杨氏模量,精度优于平均值的1%。而使用静态技术在同一种合金上测量的精度仅能达到5%到7%之间。这些结果充分说明了两种方法在精度上的巨大差异。因此,要获得高精度、高重复性的弹性模量数据,对测试方法、设备状态和操作规范都有极高要求。这正是专业检测实验室的核心价值所在。
精工博研测试技术(河南)有限公司(原郑州三磨所国家磨料磨具质量检验检测中心),央企,国字头检测机构,专业的权威第三方检测机构,专业检测材料弹性模量,可靠准确。欢迎沟通交流,电话19939716636
研究者们推荐将脉冲激励法因其高精度和简便性,作为常规质量控制工作的首选。而连续激励法则更适合用于对材料进行更全面的弹性表征研究。脉冲激励法的一个主要好处是,它无需进行节点分析即可确定共振频率。相反,静态法被认为不适合质量控制工作,因为它耗时耗力,属于劳动密集型技术。
动态法和静态法测量结果的差异背后,存在着根本的物理原因。
那么,在实际应用中该如何选择?答案取决于应用场景。如果应用是高负载且静态的,例如建筑、船舶或桥梁结构,尽管静态法不确定度较高,但它仍然是更合适的方法。反之,如果应用涉及动态过程,如弹道侵彻或弹性波传播,那么就应当采用动态方法来评估材料的弹性常数。


 首页
首页
 检测领域
检测领域
 服务项目
服务项目
 咨询报价
咨询报价