介电常数：从物理基础到测量实践的深度解析

电磁场与物质的相互作用，是理解材料电学特性的基石，其核心由麦克斯韦方程组所描述。当我们探讨电介质材料时，一个无法回避的核心概念便是其在外加电场下的响应——极化（Polarization, P）。极化现象描述了由外电场 E 诱导产生的电位移 D。

$$ P = D - /epsilon_0E = (/epsilon_{/mathrm{r}}^*/epsilon_0 - /epsilon_0)E /quad (9.68) $$

此处的 ε₀ 是真空介电常数，一个基本物理常数 (ε₀ = 8.854×10^-12 F/m)。而真正揭示材料内在属性的，是复介电常数张量 ε = ε₀ε_r = ε’ - iε’'。它并非一个简单的标量，而是与温度、电场频率紧密相关；对于各向异性材料，其数值还依赖于电场矢量 E 的方向。复介电常数的频率依赖性，是洞察材料微观动态的关键窗口，如图1所示。

为了更便捷地比较不同材料，我们通常使用相对复介电常数 ε_r，它是材料复介电常数与真空介电常数的无量纲比值：ε_r = ε^* / ε₀ = ε’_r - iε’'_r。

• 介电常数 (Dielectric Constant)：即相对复介电常数的实部 ε’_r。它表征了材料储存电能的能力。在技术文献中，它也可能被记为 K, k, K’, k’, ε_r 或 ε’。
• 介电损耗角正切 (Dielectric Loss Tangent)：tan(δ) = ε’‘_r / ε’_r，是介电损耗（虚部）与介电常数（实部）的比值，反映了电能在材料中转化为热能的程度。

观察图1可以发现，在特定的弛豫频率 ƒ_r 处，介电常数 ε’_r 会发生一个 Δ ε’_r 的下降，与之对应的是介电损耗 ε’‘_r 出现一个峰值。这种与频率相关的响应特性，我们称之为介电弛豫 (Dielectric Relaxation)。一种电介质材料可能存在多种介电弛豫过程，每一种都由其独特的分子机制决定，并拥有其特征性的弛豫强度 Δ ε’_r、损耗峰 ε’'_r 和特征频率 ƒ_r。

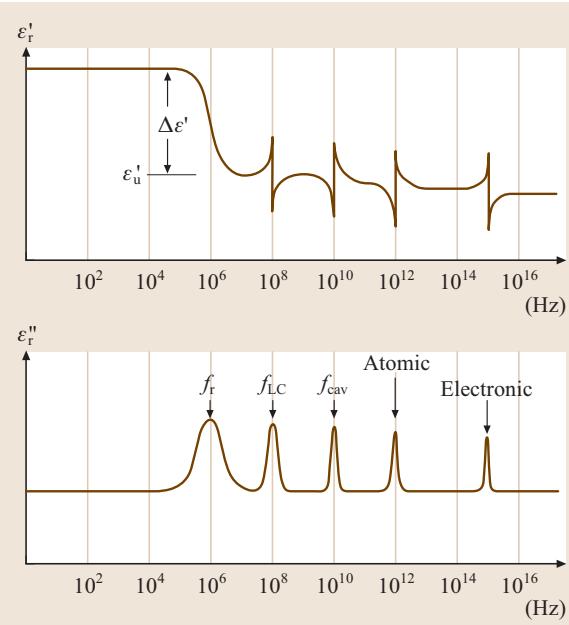图1 复介电常数的实部ε’_r和虚部ε’'_r随频率变化的典型曲线，展示了在弛豫频率ƒ_r处的单弛豫过程。

需要明确的是，介电弛豫不同于分子振动能级和电子能级间的共振跃迁，也应与测量电路本身可能引入的谐振行为区分开来。

介电弛豫 (Dielectric Relaxation)

介电弛豫的物理起源与电传导有着本质区别。电传导依赖于载流子（电子、离子、空穴）在电场作用下的宏观迁移；而介电弛豫则源于电偶极子对外加电场的取向响应。

• 非极性材料 (Nonpolar Materials)：其偶极矩仅在外电场施加时才被诱导产生。
• 极性材料 (Polar Materials)：自身拥有永久性的分子偶极矩。这类材料能展现出多种弛豫过程，如协同畸变极化、局域旋转极化和界面极化等，这些都是常见的弛豫机制。

对于最简单、仅包含单一弛豫时间 τ_r 的情况，其行为可用德拜模型 (Debye’s model) 来描述：

$$ /epsilon^{*} / /epsilon_{0} = /epsilon_{/mathrm{u}}^{/prime} + /frac{/Delta/epsilon_{/mathrm{r}}}{1 + /mathrm{i}/omega/tau_{/mathrm{r}}} /quad (9.69) $$

其中，ε’_u 是高频极限下的介电常数。如图1所示，当频率 ƒ >> ƒ_r 时，永久偶极子的贡献消失，此时 ε’_r = ε’_u。

在复合材料或复杂体系中，多种弛豫过程可能同时存在，导致极其复杂的介电行为。此时，单一的德拜模型不再适用，需要采用更普适的模型，例如 Havriliak-Negami (HN) 松弛函数，它能很好地从现象学上描述分子液体、固体和玻璃形成体的介电弛豫数据：

$$ /epsilon^{*} / /epsilon_{0} = /sum_{k}/left(/epsilon_{/mathrm{u}}^{/prime} + /frac{/Delta/epsilon_{/mathrm{r}}}{[1 + (/mathrm{i}/omega/tau_{/mathrm{r}})^{/alpha}]^{/gamma}}/right), /quad k = 1,2,3/ldots /quad (9.70) $$

这里的参数 α 和 γ (0 < α ≤ 1, 0 < αγ < 1) 分别描述了介电函数谱的对称性展宽和非对称性展宽。当 α = γ = 1 时，HN 方程就退化为德拜方程。尽管 HN 方程常被看作是一个经验公式，但近年来的理论模型已将其参数与微观动力学联系起来：α 与分子位移的时间间歇性有关，而 γ 则对应于材料局部性质中长寿命的空间涨落（即“动态非均匀性”或“动态簇”）。这为我们理解拟合参数的物理意义提供了深刻的洞察。

无论介电弛豫背后的具体分子机制为何，图1所展示的 ε_r^* 随频率变化的现象学规律，为我们选择合适的测量方法以及分析大多数电介质材料的属性提供了通用指南。

根据图1的介电谱，我们可以将其划分为几个特征区域：

1. 低频区 (ƒ << ƒ_r)：在此区域，电偶极子有足够的时间响应交变电场，几乎没有相位滞后。介电损耗极小，而极化强度达到最大值。其具体数值取决于热扰动下的分子取向统计分布和外加场强。在更高场强下，所有偶极子可能完全对齐，出现极化饱和，此时电场诱导的极化远超热效应，导致非线性的介电响应。
2. 弛豫频率区 (ƒ ≈ ƒ_r)：分子偶极子的转向速度跟不上交变电场的步伐，开始出现明显的相位滞后。它们对 ε’_r 的贡献减小。这种 E 场与 P 场之间的时间延迟或相位差，正是介电损耗的来源，并在 ƒ_r 处达到峰值。
3. 高频区 (ƒ >> ƒ_r)：特定类型的分子偶极子完全无法跟随电场的变化，因此不再对 ε’_r 和 ε’‘_r 产生贡献，此时 ε’_r 衰减至高频介电常数 ε’_u。

一个关键点是，弛豫过程总是导致 ε’_r 随频率升高而降低。从电路角度看，偶极弛豫可以很好地由一个电容 C_s 和一个电阻 R_s 并联的等效电路来描述（如图2所示）。C_s 和 R_s 均可通过实验测量，并直接关联到材料的介电特性 ε’_r 和 ε’'_r。

共振跃迁 (Resonant Transitions)

在图1中，高于 ƒ_r 的频率下 ε’_r 可能出现的快速振荡，预示着共振现象的发生。与弛豫相似，共振跃迁也伴随着介电损耗峰。然而，共振的显著特征是 ε’_r 在共振频率处的奇异行为。从介电计量的角度看，最重要的两种共振是串联谐振和腔体谐振，它们分别常见于射频和微波频段。

串联电感-电容电路谐振

任何实际的测量电路都包含互连导线，这会引入不可避免的残余电感 L_R。因此，在测量一个电容 C_s 时，必然存在一个特定的频率 ƒ_LC = 1 / (2π√(L_RC_s))，在该频率点会发生串联谐振。其等效电路为一个 C_s 与 L_R 串联，同时还存在一个由导线有限电导率引起的残余电阻 R_R（如图2所示）。

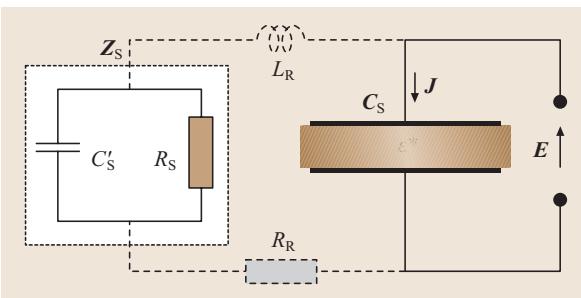图2 电介质材料的等效电路模型

在 ƒ_LC 处，能量主要集中在电感 L_R 的磁场（电流）中，而非电容 C_s 的电场内，因此这种谐振条件通常不用于精确测量介电常数。相反，这一现象是介电测量中常见的系统误差来源。其典型特征是，当频率趋近 ƒ_LC 时，测得的复阻抗会急剧下降至 R_R，同时伴随着相角从 -φ 到 +φ 的突变。如果在等效电路分析中忽略了 L_R，那么在 ƒ_LC 附近测得的 C_s 值会显得异常巨大，这很容易被错误地解读为介电常数的“表观”急剧增加（如图1所示的伪峰）。准确识别并扣除这类测量假象，对获得材料真实的介电性能至关重要。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测介电性能检测，可靠准确。欢迎沟通交流，电话19939716636

介质谐振 (Dielectric Resonance)

当电介质样品的尺寸 (l) 与其内部的导波波长 λ_g = λ₀ / √(ε’_r) 相当时，透射波与反射波的叠加会形成驻波，即所谓的腔体谐振或介质谐振。在谐振频率下，电磁能量高度集中在电介质内部的电场中。因此，基于介质谐振器的测量技术是测定低损耗材料介电常数最精确的方法之一。

红外与光学跃迁

当电磁波频率上升至 10¹² Hz 及以上时，其与物质的相互作用进入了量子领域，会引起电子、振动和转动分子能级之间的量子化共振跃迁。这些跃迁同样导致介电常数的奇异行为和相应的吸收，可通过各种量子光谱技术进行观测，构成了现代化学与物理学的重要分支。在光频段，材料的介电特性通常用复折射率 n = √ε 来描述，而非介电常数。