介电常数测量技术：从集总参数到微波网络的综合指南

精确表征材料的复介电容率 (ε_r^*) 对高频电路设计、天线开发及新材料研究至关重要。测量技术本身并非一成不变，其选择与测试频率和样品尺寸的相对关系紧密相连。广义上，我们可以将这些技术划归两大阵营：

1. 集总参数模型适用区：在这一频率范围，电磁波的波长远大于介电样品的物理尺寸，因此样品可被简化为分立的集总参数元件（如电容、电阻）进行分析。
2. 分布参数模型适用区：当频率升高，电磁波波长缩短至与样品尺寸相当的量级，波在样品内的传播效应变得不可忽略。此时，必须将样品视为一个分布参数系统来处理。

基于集总参数模型的介电测量

在波传播效应可以忽略不计的低频段，我们可以通过测量等效弛豫电路的复阻抗 Z_s 来确定其等效电容 C_s，进而推算出材料的相对复介电容率 ε_r^*。

当一个电容器被介电材料填充时，其电容变为 C_s。根据定义，相对复介电容率 ε_r^*(ω) 可以表示为：

ε_r^*(ω) = ε_r′(ω) - iε_r″(ω) = C_s(ω) / C₀

其中，C₀ 是空测试夹具（或称空电容池）的电容，ω 是角频率 (ω = 2πf)。

若对该电容器施加一个正弦电场 E(ω) = E₀exp(iωt)，通过测量电路的复阻抗 Z_s 便可确定介电常数：

1/Z_s(ω) = iωC_s ε^*(ω) = 1 / [iωZ_s(ω)C₀]

若采用一个更贴近物理实际的等效电路模型——一个理想电容 C_s′ 与一个电阻 R_s 并联，那么其复阻抗的倒数（导纳）为：

1/Z_s(ω) = 1/R_s + iωC_s′

由此，我们可以直接得到 ε_r′ 和 ε_r″ 的表达式：

ε_r′ = C_s′/C₀ ε_r″ = 1 / (ωR_sC₀)

这里的 C₀，即“电容池常数”，通常根据样品的几何形状计算得出，或通过测量已知介电常数的标准物质来标定。市售的介电测试夹具通常会由制造商提供精确的 C₀ 值及相应的误差校正公式。

四端法阻抗测量技术

在频率高达约 10⁸ Hz 的范围内，可以采用四端（4T）阻抗分析仪来测量样品的复阻抗，并利用上述公式计算介电常数。四端法的核心在于能够直接对样品的电流和电压进行高灵敏度的相位测量。近年来，集成了傅里叶相关分析、介电转换器和阻抗分析功能的先进系统已经商业化。这些现代介电测量仪器将数字频率合成器、正弦波相关器和锁相放大器等模块整合于一体，能够实现从 10^-12 Ω 到 10¹³ Ω 的超宽范围自动阻抗测量，相应地，其电容测量分辨率可逼近 10^-15 F。为保证精度，所有仪器都应遵循制造商的建议，使用适当的阻抗标准件进行校准。

典型的介电样品采用平行板或圆柱形电容器结构，其电容值通常在 10 pF 到几百 pF 之间。标准测量程序推荐使用带保护电极（G）的三端（3T）测试盒，这种设计能有效抑制边缘电场和杂散电场对测量结果的干扰。将一个三端测试盒连接到四端阻抗分析仪的最佳方式如图1所示。

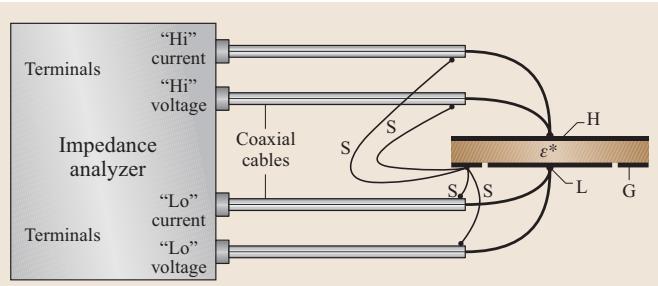
图1：3T测试盒与4T阻抗分析仪的连接。(H)和(L)分别是高、低电位电极；'G’是保护电极；(S)是同轴电缆屏蔽层的电流回路连接点。

“High”端（高电位）的电流和电压端子应通过同轴电缆直接连接到无保护的电极’H’。而“Low”端（低电位）的电流和电压端子则连接到被保护电极环绕的中心电极。一个关键细节是，所有同轴电缆屏蔽层构成的返回电流回路’S’应尽可能短，并在一个公共点连接到保护电极’G’。这个返回电流回路对于精确的阻抗测量，尤其是在频率超过 1MHz 时，是绝对必要的。如果采用没有保护电极的两端（2T）配置，屏蔽层’S’则应简单地共同接地。

另外，材料的介电常数、介电损耗和弛豫频率都与温度相关。因此，在测量过程中精确控制并维持样品温度恒定（等温条件）是保证数据可靠性的基本要求。

基于同轴线反射法的阻抗测量

四端法配置的一个固有局限是，连接电缆的残余电感 L_R 会引入额外的电路阻抗，并在 f_LC ≈ 1 / (2π√(L_RC_s′)) 处产生串联谐振，从而限制了可用的频率上限。这个谐振点通常出现在 30 MHz 以上。要在更高频率下测定阻抗，就需要借助微波技术和精密传输线，即同轴线反射法。这类技术可以将测量的参考面直接设置在样品所在的位置，从而极大地消除了由 L_R 引起的传播延迟。

其原理是：当一个特性阻抗为 Z₀ 的传输线被一个阻抗为 Z_s 的介电样品终端时，两者之间的阻抗不匹配会导致入射波发生反射。Z_s 与复反射系数 Γ 之间的关系如下：

Γ = (Z_s - Z₀) / (Z_s + Z₀)

从该式可以推知：当传输线被短路 (Z_short = 0) 终端时，Γ = -1；当开路 (Z_open = ∞) 终端时，Γ = 1；而当负载匹配 (Z_s = Z₀) 时，Γ = 0，即没有反射。这三种终端状态——短路（Short）、开路（Open）和匹配负载（Load），正是用于校准、建立测量参考面以及确保反射系数测量准确性的标准件。

在射频和微波频段，存在多种针对特定用途和应用的同轴线配置。其可用频率范围受限于同轴结构中第一类圆形波导传播模式的激励。减小内外导体的直径可以提高可用的最高频率。以下是几种以 50Ω 为特性阻抗的、常用于微波测试的同轴线配置简介。

精密 APC-7 mm 配置

APC-7（Amphenol Precision Connector-7 mm）连接器在内外导体之间使用空气作为介电质。它能提供从直流到 18 GHz 范围内最低的反射系数和最佳的测量可重复性，是计量和校准等要求最苛刻应用的首选。其内导体直径 d = 3.02 mm，外导体直径 D = 7.00 mm，这决定了其 50Ω 的特性阻抗。

精密 APC-3.5 mm 配置

3.5 mm 配置同样使用空气作为介电质，其无模式传输的频率上限可达 34 GHz。

精密 2.4 mm 配置

由惠普（Hewlett Packard）和安费诺（Amphenol）为高达 50 GHz 的应用开发的同轴配置。它可以通过适配器与 APC 3.5 mm 连接器配接。2.4 mm 同轴线提供三种质量等级：通用级、仪器级和计量级，分别适用于经济型元件与电缆、要求高重复性和长寿命的测量应用，以及要求最高性能和可重复性的校准应用。

1.85 mm 同轴配置

该配置由惠普（现安捷伦科技/是德科技）于1980年代中期开发，旨在实现高达约 65 GHz 的无模式性能。惠普于1988年将其设计公开，以鼓励该连接器类型的标准化。如今，主要用于科研领域的各种制造商提供了少量基于此标准的设备和仪器。1.85 mm 连接器可与 2.4 mm 连接器配接。

1.0 mm 同轴配置

为支持高达 110 GHz（接近光频）的传输而设计。1.0 mm 同轴配置及其配套的适配器和连接器，是精密微波元件制造领域的一项重大成就。

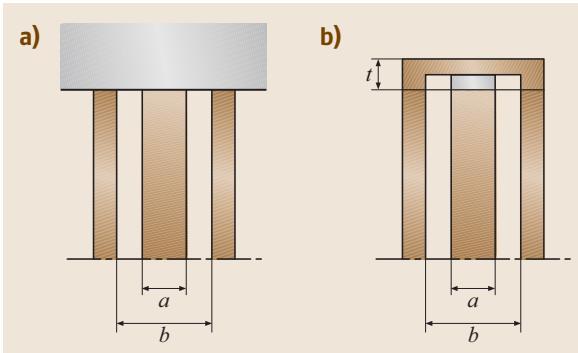
图2：(a) 开路端和 (b) 短路端同轴测试夹具

基于这些同轴结构，衍生出了一大家族用于介电测量的测试夹具。开路同轴探头（图2a）被广泛用于表征块状固体材料和液体，并且有商业化产品（如 Agilent/Keysight, Novocontrol 的介电探头）。测量时只需将探头端面接触样品平整的表面，或将探头浸入液体样品中即可，非常便捷。

而短路端接探头（图2b）则更适合薄膜样品的测试。在测量中，常使用介电常数已精确已知的材料（如空气、去离子水）作为参考，以校正因测量配置与校准配置差异所引入的系统误差。

如果弛豫电路依然满足集总参数条件，那么 ε_r′ 和 ε_r″ 可通过结合阻抗和反射系数的公式得到：

ε_r′ = -2|Γ|sinφ / [ωZ₀C₀(1 + 2|Γ|cosφ + |Γ|²)] tanδ = ε_r″/ε_r′ = (1 - |Γ|²) / (-2|Γ|sinφ)

在实践中，上述传统的集总参数公式和测试流程，其精度上限对应于样品阻抗降低至同轴线特性阻抗约十分之一（0.1）的频率点。由于标准同轴线的特性阻抗为 50Ω，这意味着集总参数电路可用的最低阻抗值约为 5Ω。因此，频率上限 f_max ≈ 1 / (10πC_s′)。对于 APC-7 配置，根据样品的介电常数和厚度，该频率上限通常低于 5 GHz。当频率 f > f_max 时，波的传播效应导致电场在样品内部呈空间分布，样品再也不能被视为一个集总电容，必须作为微波网络进行分析。

基于微波网络分析的介电测量

微波网络分析仪通过测量入射、反射和透射的电磁波来表征器件或材料。如图3所示，反射波在端口1（Port 1）测量，透射波在端口2（Port 2）测量。

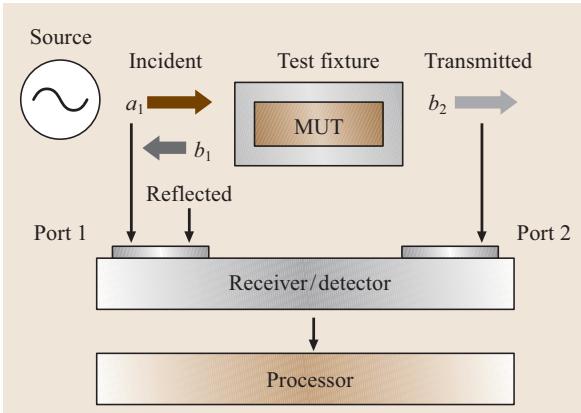
图3：网络分析仪的框图

只要知道这些波的幅度和相位，就可以量化待测材料（MUT）的反射和透射特性，并结合测试夹具的尺寸信息，最终求解出其介电常数。在微波领域，由于直接测量高频总电压或总电流非常困难，通常转而测量复数散射参数（Scattering parameters），即S参数（S₁₁, S₁₂, S₂₁, S₂₂）。S参数是相对于入射波进行归一化的，因此其测量结果与绝对功率和源的功率频率漂移无关。S参数定义如下：

b₁ = S₁₁a₁ + S₁₂a₂ b₂ = S₂₁a₁ + S₂₂a₂

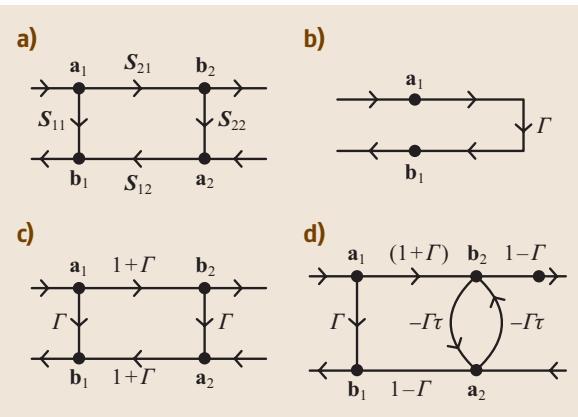
图4：S参数信号流图：(a) 双端口网络, (b) 负载终端, © 并联导纳, (d) 部分填充介电材料的传输线

图4a展示了一个通用双端口网络的信号流图。其中 a₁ 和 a₂ 是进入网络的波的复振幅，b₁ 和 b₂ 是离开网络的波的复振幅。S参数的命名规则是，第一个数字代表能量出射的端口，第二个数字代表能量入射的端口。因此，S₂₁ 表征的是从端口1施加激励后，从端口2出射的能量。当两个数字相同时（如S₁₁, S₂₂），则表示反射测量。例如，图4b中，由于没有波透射到端口2（b₂=0），负载的反射系数 Γ = b₁/a₁ = S₁₁。

双端口透射-反射法

将一个介电样品部分填充到一段同轴空气线中（如图5），会引起阻抗失配和多次波反射，这个系统可以被建模为一个双端口网络。

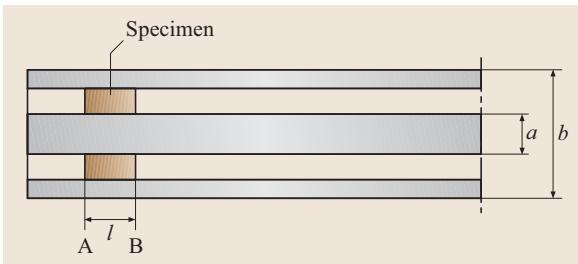
图5：用于透射-反射法的测试夹具

对于一个介电常数为 ε_r^* 的样品，在参考面A和B处的散射参数 S₁₁ 和 S₂₁ 可以从图4d的信号流图中推导得出：

S₁₁(ω) = (1 - τ²)Γ / (1 - τ²Γ²) S₂₁(ω) = (1 - Γ²)τ / (1 - τ²Γ²)

其中，对于非磁性介质，复反射系数 Γ 和传输系数 τ 分别为：

Γ = (Z_s - Z₀) / (Z_s + Z₀) = (1 - √ε_r) / (1 + √ε_r) τ = e^-iγl

而传播常数 γ = iω/c * √ε_r^*。

使用一个内径 d = 3.02 mm、外径 D = 7.0 mm 的 APC-7 无支撑珠同轴空气线作为样品支架，可以测量高达 18 GHz 的介电常数。这种方法对样品加工精度要求极高，样品必须与同轴线的内外导体尺寸精确匹配。

获取高频下可靠的介电性能数据，不仅需要精密的仪器，更依赖于对测量原理的深刻理解和严谨的样品制备与操作。这正是专业检测实验室的核心价值所在。 精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测高频介电性能，可靠准确。欢迎沟通交流，电话19939716636

单端口反射法

网络分析在另一项高频介电计量中的重要应用是，在短路端接的同轴测试夹具中（图2b）测量薄膜的介电常数。

将待测样品视为一段带有电容的传输线，其S参数和阻抗表达式为：

S₁₁(ω) = (Γ + τ) / (1 + Γτ) Z_s = [x cot(x)] / (iωC_s) + iωL_s

其中，波传播参数 x = ωl√ε_r^* / 2c。最终，复介电容率可以通过求解以下超越方程得到：

ε_r^* = [x cot(x)] / {iωC₀[Z₀(1 + S₁₁) / (1 - S₁₁) - iωL_s]}

这些方程的有效性已经在数值和实验上得到验证，其频率上限可达第一个腔体谐振点 f_cav：

f_cav = c / [l * Re(√ε_r^*)] ≈ 121 / [√ε_r′ (GHz)]

这里 Re 表示对复介电容率平方根取实部，l 是传播长度（对于图2b中的APC-7测试夹具，l = 2.47 mm）。举个例子，如果一个样品的介电常数为100，其腔体谐振频率 f_cav 大约在 12 GHz。

谐振腔法

谐振法是测定介电常数最精确的方法之一，但它通常要求材料具有非常低的介电损耗 (ε_r″ < 10^-3) 以便能激发出尖锐的谐振峰。其测量频率通常局限于微波频段的几个离散点。

一种相对简单且常用的谐振法是谐振腔微扰法。图6展示了一个由一小段矩形波导构成的腔体测试夹具。波导两端用法兰盘固定或焊接导电板，形成一个谐振盒。端板上的小耦合孔用于馈入和引出微波能量。在相对的腔壁中心开有通孔，用于插入介电样品，并确保样品位于电场最强的区域。

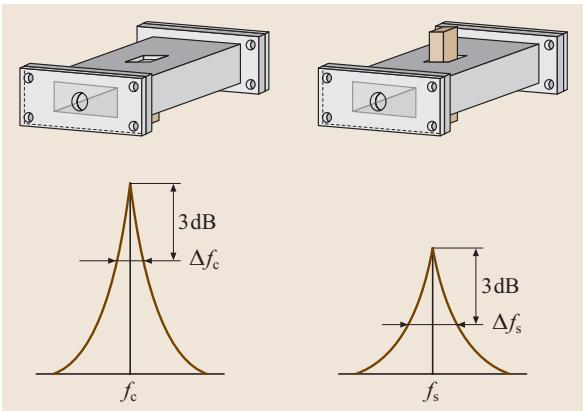
图6：(a) 空测试夹具和 (b) 置入样品后测得的S₂₁参数

将测试夹具连接到网络分析仪（如图3），谐振表现为 |S₂₁| 参数在谐振频率处出现一个尖锐的峰值。当介电样品被插入空腔（空气填充）后，谐振频率会从 f_c 下降到 f_s，而半功率点（即低于 |S₂₁| 峰值 3dB 处）的带宽 Δf 会从 Δf_c 增加到 Δf_s（如图6所示）。谐振频率的偏移量与样品的介电常数实部相关，而带宽的展宽（对应品质因数 Q 的降低）则是由介电损耗引起的。

该方法需要测量 f_c, Δf_c, f_s, Δf_s，以及空腔体积 V_c 和样品体积 V_s。空腔和置入样品后腔体的品质因数 Q 分别为：

Q_c = f_c / Δf_c Q_s = f_s / Δf_s

介电常数的实部和虚部则由下式给出：

ε_r′ = [V_c(f_c - f_s)] / (2V_sf_s) ε_r″ = (V_c / 4V_s) * (1/Q_s - 1/Q_c)

微扰法的一个前提条件是样品体积必须远小于腔体体积 (V_s < 0.1V_c)，否则会降低精度。同时，样品必须对称地放置在电场最大处。尽管有这些限制，但与其他谐振法相比，微扰法具有精度高、计算简单、样品易于制备（圆柱、长方体或球形）等优点。这些形状也是陶瓷、铁氧体和有机绝缘材料在微波通信和电力输配应用中的基本形态。

在技术文献和标准中还描述了大量其他的谐振技术，每种技术都在特定的频段、场分布和材料损耗特性方面有其独特的应用领域，例如：

• 开槽腔谐振器：适用于在X波段测量片状低损耗材料。
• 开槽柱介质谐振器：同样适用于片状材料，其优点是可以在较低频率下工作而无需使用大尺寸样品。
• 平行板谐振器：允许在更低的频率下进行测量，因为介质内部的导波波长被压缩了。
• 全板谐振技术：常用于测定印刷电路板（PCB）用覆铜板的介电常数。