金属-半导体接触电阻：机理、表征与测量技术

日期：2025-07-23 浏览：5

金属-半导体接触电阻：机理、表征与测量技术

在半导体器件中，欧姆接触是连接内部有源区与外部电路或其他器件的生命线，其性能优劣直接关系到整个器件的电学表现。从物理学家或工程师的视角来看，一个理想的欧姆接触应具备以下特征：

呈现双极性的线性 I-V 特性。
为少数载流子提供近乎无限的复合速率。
相较于有源区，其自身的电压降可忽略不计。
不产生少数载流子注入。

然而，在实际的金属-半导体界面上，完美的欧姆接触并非天然形成。功函数差异与界面态的存在，往往会形成一个能量壁垒，即肖特基势垒。如何让电子高效地跨越这道“鸿沟”，是实现低电阻欧姆接触的核心挑战。

跨越界面势垒的三种核心载流子输运机制

当金属薄膜（例如通过蒸发工艺）沉积在n型半导体上时，若两者功函数与电子亲和能匹配不佳，便会在半导体一侧形成势垒高度为 Φ_B 的阻碍。即使精心选择材料体系，一个或大或小的势垒在多数情况下也难以避免。电子要想从半导体进入金属，必须克服或穿透这个势垒。其主要路径可归纳为以下三种电流传导机制。

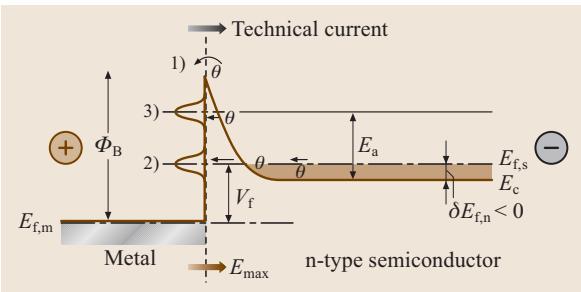
图1. 高掺杂简并n型半导体与金属接触在正向偏压下的能带图（金属电位高于接地的n型半导体）

热电子发射 (Thermal Emission)：电子依靠自身的热能（与kT相当）来“翻越”高度近似为 Φ_B 的势垒。只有少数高能电子能够成功越过，因此这种机制效率低下，形成的接触电阻很大，在室温下常表现出明显的整流特性。顾名思义，该过程对温度高度敏感，在高温下呈指数级增强。
场致发射或隧穿 (Field Emission or Tunneling)：这是一种纯粹的量子力学现象。当半导体掺杂浓度极高（远超 10¹⁸ cm^-3）时，界面处的空间电荷区会变得极窄（小于10 nm）。如果势垒宽度小于电子的德布罗意波长，电子便能利用其波动性，在不损失能量的情况下直接“穿透”势垒。该过程几乎与温度无关，即便在极低温下也同样有效，因为量子隧穿无需热能激活。
热场发射 (Thermal Field Emission)：此机制介于上述两者之间，常见于中等掺杂水平的半导体。一部分电子先被热能激活到一个较高的能级，虽然能量仍不足以越过势垒顶峰，但在此位置，它们需要隧穿的势垒变得更窄、更低。与纯粹的热发射或场致发射相比，电子面对的是一个等效上更易穿越的障碍。可以看作是热激发与隧穿两种机制的串联协作。

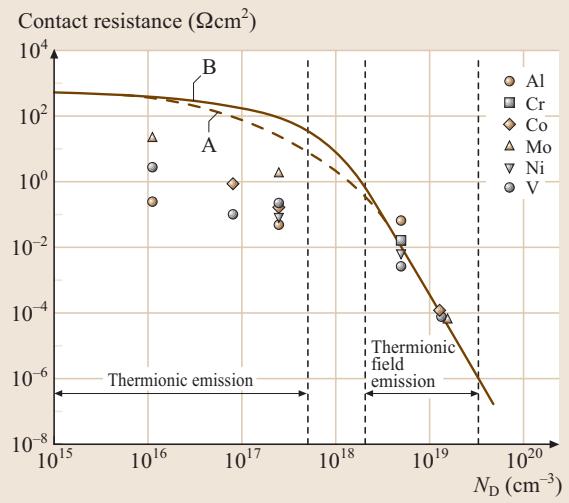
图2. 不同金属在n型硅上的接触电阻与硅掺杂浓度N_D的关系

上图清晰地展示了掺杂浓度对接触电阻（单位：Ω·cm²）的决定性影响。随着掺杂浓度提升，电流传导机制逐渐从热电子发射过渡到场致发射（隧穿），接触电阻急剧下降。在工程应用中，接触电阻率通常要求低于 10^-5 Ω·cm²。为达到此目标，掺杂浓度需要超过 10¹⁹ cm^-3，以确保隧穿效应占据绝对主导。目前，先进工艺已能实现低于 10^-7 Ω·cm² 的接触电阻率。

接触电阻的构成：比接触电阻与总接触电阻

在讨论接触电阻时，有必要精确区分两个概念：

比接触电阻 (Specific Contact Resistance, R_c,spec 或 ρ_c)，单位为 Ω·cm²。它特指金属与半导体界面本身所贡献的电阻，是衡量界面物理特性的核心参数。
总接触电阻 (Total Contact Resistance, R_c)，单位为 Ω。它除了包含比接触电阻外，还计入了半导体材料的扩展电阻 (Spreading Resistance)。扩展电阻的大小与电流在触点下的分布路径（即电流线）密切相关，因此受到接触电极的几何形状影响。

根据电流扩展方式，接触可分为两类：

垂直电流接触：电流在接触区域内分布较为均匀，例如激光器的顶部电极或双极晶体管的发射极接触。
横向电流接触：电流在接触长度上分布极不均匀，例如双极晶体管的基极接触或场效应晶体管（FET）的源/漏极接触。

相应的，接触电阻的测量技术也需根据接触的几何构型来选择。测量的核心目标是从数值通常偏高的总接触电阻中，精确地提取出数值较低的比接触电阻，从而为优化接触工艺（如退火）提供可靠依据。

接触电阻的精确测量方法

开尔文结构 (Kelvin Configuration) 测量欧姆接触时，普遍采用开尔文结构（即四探针法）来消除测量探针与接触焊盘之间附加电阻带来的误差。其原理是使用两根探针施加恒定电流，再用另外两根独立的探针在尽可能靠近待测区域的位置测量电压。

Cox & Strack 方法 对于电流近乎均匀流入的垂直接触，可以采用Cox和Strack提出的方法。该方法通过在半导体上制作一系列不同直径的圆形接触点，来区分比接触电阻和扩展电阻的贡献。

传输线模型 (Transmission Line Model, TLM) 对于电流非均匀流动的横向接触（尤其是在薄半导体层上），由Berger提出的传输线模型（TLM）是一种功能更强大、应用更广泛的方法。

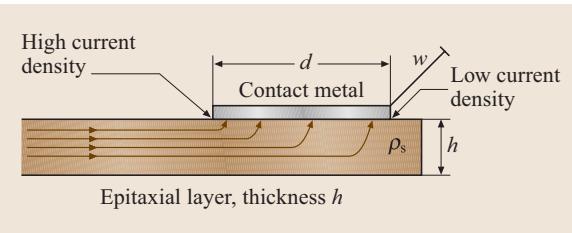
图3. 宽度为w、长度为d的横向接触在厚度为h的薄外延层上的电流分布示意图

如图3所示，电流在横向接触下的分布是复杂的。假设半导体薄层具有电阻率 ρ_s (Ω·cm) 和薄层电阻 R_s (Ω/□)，其中 R_s = ρ_s / h。在实际器件中，薄层厚度 h 通常远小于接触长度 d。

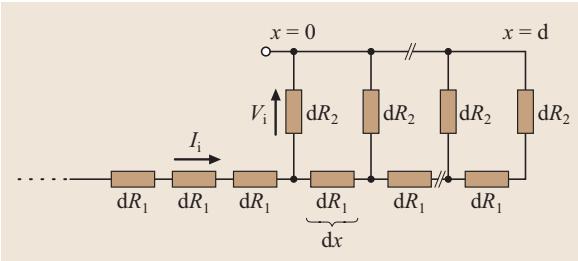
图4. 基于图3电流分布的横向欧姆接触等效电路图

这种结构可以等效为一个传输线网络（图4）。外延层的电阻由一系列差分单元 dR₁ 串联而成，而比接触电阻 ρ_c 则由分布式的垂直单元 dR₂ 代表。总接触电阻 R_c 定义为接触区域起始端的电压与流入结构的总电流 I 之比。

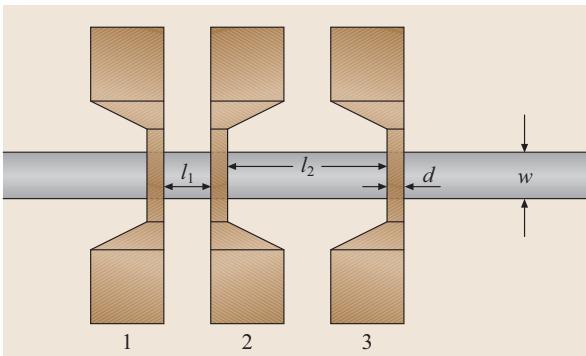
图5. 用于提取薄层电阻R_s和总接触电阻R_c的TLM测试结构掩模版

为了从测得的总接触电阻 R_c 中提取出比接触电阻 ρ_c，需要求解描述该传输线模型的微分方程，最终得到一个隐式方程：

$$ R_{/mathrm{c}} = /frac{1}{w}/sqrt{/left[R_{/mathrm{s}}/left(/rho_{/mathrm{c}} + 0.2R_{/mathrm{s}}h^{2}/right)/right]} /times /coth /left(/sqrt{/frac{R_{/mathrm{s}}}{/left(/rho_{/mathrm{c}} + 0.2R_{/mathrm{s}}h^{2}/right)}} d/right) $$

要解出此方程中的 ρ_c，必须先测得 R_c 和 R_s，并精确获知测试结构的几何常数 w、h 和 d。

R_s 和 R_c 的测量可以通过一个包含多个接触条的TLM测试结构（图5）来完成。通常需要进行两次开尔文测量：

在相距为 l₁ 的接触条1和2之间施加电流 I (mA量级)，测量其间的电压 V₁。
在相距为 l₂ 的接触条2和3之间施加相同的电流 I，测量其间的电压 V₂。

通过这两个电压值 V₁、V₂ 和恒定电流 I，可以计算出薄层电阻 R_s 和每个接触条下方的总接触电阻 R_c：

$$ R_{/mathrm{s}} = /frac{V_1 - V_2}{l_1 - l_2}/frac{w}{I} $$

$$ R_{/mathrm{c}} = /frac{1}{2}/left(/frac{V_1}{I} -l_1/frac{R_{/mathrm{s}}}{w}/right) $$

获得 R_s 和 R_c 后，即可代入前述的隐式方程求解比接触电阻 ρ_c。值得强调的是，接触间距 l₁ 和 l₂ (通常在 1-100 μm 范围) 必须进行高精度测量（亚微米级），否则会给 ρ_c 的计算带来巨大误差，尤其是当 ρ_c 低于 10^-6 Ω·cm² 时。因此，要获得可靠的接触电阻数据，对测试结构的加工精度和测量手段都有极高要求。这正是专业检测实验室的核心价值所在。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测半导体电学性能，可靠准确。欢迎沟通交流，电话19939716636

衍生参数：传输长度与传输电阻

对于电学长接触（例如 d = 40 μm），可以定义两个重要的衍生参数：

传输长度 (Transfer Length, L_T)：定义为 L_T = √(ρ_c / R_s)。它形象地描述了电流从半导体外延层“传输”进入金属接触所需的典型长度。在实际设计中，接触电极的长度没有必要超过三倍传输长度，因为更长的部分对降低接触电阻的贡献已微乎其微。
传输电阻 (Transfer Resistance, R_T)：定义为 R_T = √(R_sρ_c) (Ω·mm)。该参数表征了对于给定宽度 w 的电学长接触，所能达到的最低接触电阻。例如，对于场效应晶体管（FETs），其传输电阻值应低于 0.2 Ω·mm。