半导体掺杂与载流子浓度的测量方法

在半导体器件的研发与生产中，精确掌握材料的掺杂浓度 (Dopant Concentration) 与载流子浓度 (Carrier Concentration) 是至关重要的环节。电容-电压 (Capacitance-Voltage, C-V) 分析法是实现这一目标的主流技术，它不仅能提供平均的载流子浓度信息，更核心的优势在于能够描绘出材料内部随深度变化的浓度分布剖面。

执行C-V分析通常借助LCR测试仪，该设备能同时测量样品的电容和交流电导。在评估C-V数据时，一个基本前提是样品的损耗角正切 (G/ωC) 必须足够小（通常不超过百分之几），这确保了在特定测量频率下，电容项远大于电导项的贡献，测量结果才能准确反映电容特性。

如果在一个标准频率（例如1MHz）下，损耗角正切值过高，就需要调整策略：对于存在平行漏电导的情况，应选择更高的测量频率；而对于样品串联电阻过大的情况，则应采用更低的频率。一个实用的经验法则是，选择能使损耗角正切达到最小值的频率进行测量。此外，若样品存在平行的杂散电容，必须通过设计适当的测试结构来确定其值，并在后续的C-V分析前予以扣除。

要阐明C-V方法，最简洁的模型是肖特基接触，即在n型半导体上制作金属接触。本文将围绕此模型，首先基于耗尽近似（Depletion Approximation）解释掺杂剖面的分析原理；其次，探讨由德拜长度 (Debye Length) 效应引发的深度分辨率限制；最后，针对几种关键情况——金属-绝缘体-半导体 (MIS) 结构的近表面掺杂、离子注入形成的深度剖面以及高-低掺杂突变剖面——介绍相应的修正方法。

电容-电压 (C-V) 分析原理

半导体深度掺杂剖面的基础C-V评估方法，建立在耗尽近似的核心假设之上，即空间电荷区的边缘是突变的，并且掺杂剂已完全电离。图1展示了一个理想的测试结构：在半导体顶面蒸镀一层具有确定面积 A 的肖特基接触金属，背面则制作欧姆接触。由于金属的功函数与半导体的电子亲和能存在差异，两者接触后会形成一个深度为 w 的空间电荷区。

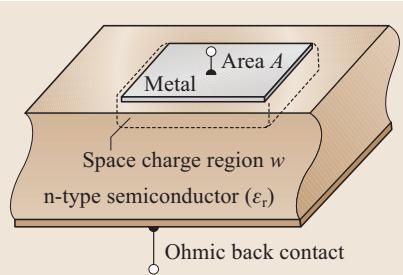
图1 n型半导体顶部的肖特基金属接触（面积 A），空间电荷区深度为 w

通过在顶部栅电极上施加反向偏压，可以控制空间电荷区的深度。在耗尽近似下，若忽略边缘效应和其他杂散电容，空间电荷区的电容可由平板电容器模型给出：

$$ C_{/mathrm{sc}} = /epsilon_0/epsilon_{/mathrm{r}}/frac{A}{w_0} /tag{1} $$

其中，εᵣ 是半导体的介电常数，ε₀ 是真空介电常数，w₀ 是零偏压下的空间电荷区宽度。图2展示了零偏压下热平衡状态的能带图。肖特基势垒高度 Φ_Bn 在半导体内部引起了 qV_bi 的能带弯曲，V_bi 是肖特基二极管的内建电压。E_c、E_v 和 E_F 分别代表导带底、价带顶和费米能级。在平衡状态下，费米能级在整个金属-半导体结构中保持恒定，表明零偏压下没有电流流动。

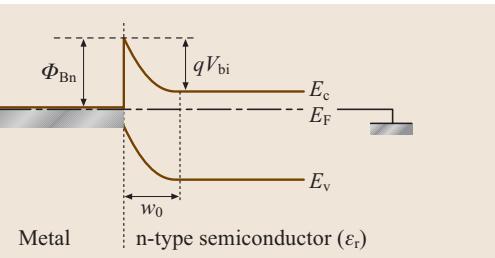
图2 零偏压下热平衡状态的金属-半导体肖特基接触能带图

当在金属电极上施加反向电压时，半导体的能带弯曲加剧，空间电荷区宽度随之增加，导致电容值根据公式 (1) 减小。图3以理想化的形式展示了耗尽近似模型，图中对比了任意假设的深度掺杂浓度剖面 N_D(w) 和由此产生的自由电子浓度剖面 n(x)。在中性区，自由载流子（此处为电子）与电离的施主原子相抵消 [N_D⁺(w) = N_D(w) = n(x)]。耗尽近似意味着，在空间电荷区的边缘，自由载流子浓度会从一个有限值突降至零。

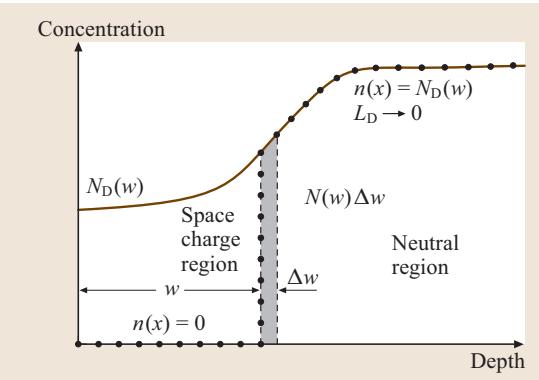
图3 耗尽近似模型下的任意深度掺杂剖面 N_D(w) 与相应的自由电子浓度剖面 n(x)

这种理想化的突变等同于假设德拜长度为零。德拜长度 L_D = (ε₀εᵣk_BT / q²n)^1/2 是一个表征屏蔽效应的特征长度，它依赖于温度 T 和载流子浓度 n，反映了载流子热运动对空间电荷畸变的修正能力。

通过求解泊松方程 div D = ρ 并对空间电荷区进行两次积分，可以推导出总能带弯曲电势 V 与空间电荷区宽度 w 的关系：V = (qN_Dw²)/(2ε₀εᵣ)（此处暂设掺杂剖面 N_D 为常数）。将此式与平板电容公式联立，求解 1/C²(V) 的表达式，再对电压 V 求导，即可得到非均匀掺杂下，载流子浓度剖面 n(x) 的表达式（在耗尽近似下，n(x) 等同于掺杂浓度 N_D(x)）：

对于 n 型半导体： $$ N_{/mathrm{D}}(x) = /frac{1}{q/epsilon_0/epsilon_{/mathrm{r}}}/frac{1}{A^2}/frac{C^3(V)}{/frac{/mathrm{d}C(V)}{/mathrm{d}V}} /tag{2} $$

对于 p 型半导体： $$ N_{/mathrm{A}}(x) = -/frac{1}{q/epsilon_0/epsilon_r}/frac{1}{A^2}/frac{C^3(V)}{/frac{/mathrm{d}C(V)}{/mathrm{d}V}} /tag{3} $$

在上述两种情况中，深度 x 同样由平板电容模型计算得出：x = ε₀εᵣA / C(V)。

C-V 方法的精度主要受栅电极面积 A 的测量精度影响。例如，面积 A 的测量误差若在 1% 以内，最终计算出的掺杂剖面误差约为 2%。此外，要保证局部电中性假设在深度剖析过程中有效，掺杂剖面的空间变化在一个德拜长度范围内应足够小。

C-V 分析的局限性：耗尽近似的挑战

C-V 剖面分析法的深度分辨率受到德拜长度的根本性限制。有限的德拜长度导致理想化的突变空间电荷区边缘实际上会发生“弥散”，这个过渡区域的宽度大约为2到3个德拜长度。如图4所示，这种现象会带来两个问题：

1. 当掺杂剖面存在陡峭的台阶时，真实的载流子分布由于弥散效应，无法同样陡峭地跟随掺杂变化，局部电中性假设失效。
2. 在进行近表面剖面分析时，即使空间电荷区仍有一定宽度，其载流子“尾巴”也可能已经延伸至界面区域。

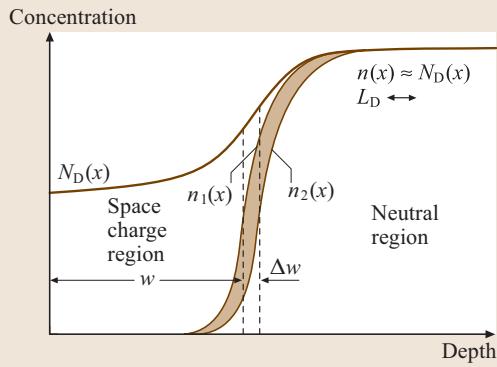
图4 考虑德拜长度弥散效应时，任意深度掺杂剖面 N_D(x) 与更真实的自由电子浓度剖面 n(x)

这两种情况都会引入剖析误差。前者使得我们无法精确测量真实掺杂剖面的陡峭程度；后者则会导致表观载流子剖面在靠近界面时（当空间电荷区宽度小于约两个德拜长度时）出现人为的升高。

虽然降低测量温度可以减小德拜长度 (L_D ~ T^1/2)，但在极低温度下，掺杂剂的电离度也会降低。这会导致测得的载流子浓度低于真实的掺杂浓度，因此该方法仅适用于非常浅的施主能级。

德拜长度修正：面向特定剖面的高级算法

为了克服德拜长度展宽效应带来的测量失真，研究人员发展了多种修正程序。以下介绍两种针对典型应用场景的修正方法。

MOS/MIS 结构的近表面掺杂剖面修正

MOS（金属-氧化物-半导体）或MIS（金属-绝缘体-半导体）结构是所有CMOS器件（如晶体管、CCD/BCCD焦平面阵列）的基石。其介电层-半导体界面附近的表面掺杂剖面必须被精确控制，因为它直接决定了器件阈值电压的数值和均匀性。

MIS结构中的绝缘层具有极高的电阻率，能有效阻断电流，这使得我们可以忽略电流项来求解泊松方程，同时考虑空间电-荷区中移动载流子的贡献。Ziegler等人基于此分析方法，将耗尽近似的适用范围拓展至MIS电容的平带点，即直至半导体表面。他们开发了一种解析的列表式修正算法，能够对由标准耗尽近似计算出的表观载流子剖面进行校正，有效避免了当剖析深度小于两个德拜长度时，表观浓度向表面人为“翘起”的现象。

图5展示了未修正剖面（点划线）与修正后剖面（圆圈）的典型对比。无论是硼掺杂还是磷掺杂的MIS电容，修正算法都给出了相对平坦的真实剖面。若无此修正，人们可能会误判退火和偏析效应导致了掺杂剂在表面的堆积。Ziegler-Klausmann-Kar剖面修正法极大地提升了平带点和表面反型点的确定精度，且该方法既适用于准静态射频测量的MIS C-V曲线，也适用于能避免表面反型的脉冲射频C-V曲线。

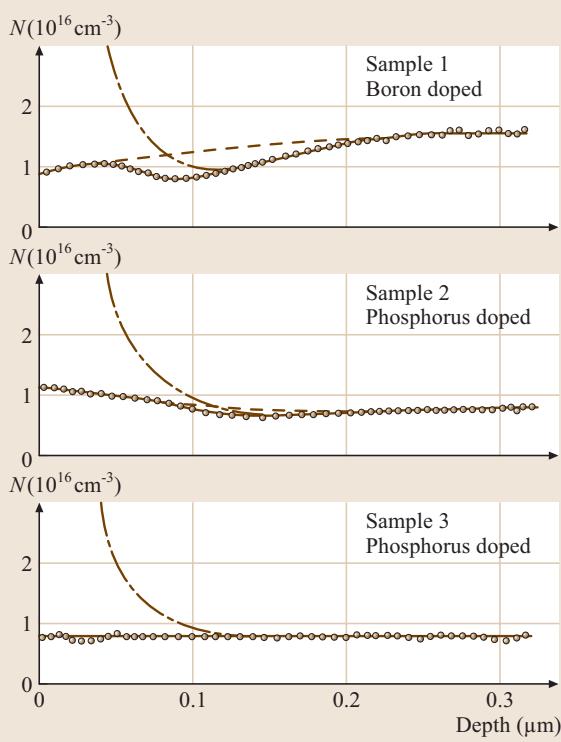
图5 硅MIS电容掺杂剖面示例。急剧上升的曲线为未经修正的表观掺杂剖面；圆圈为经过德拜长度修正后的测量结果。

离子注入剖面的测量与修正

对离子注入半导体进行深度剖析，对耗尽近似法是一个特殊的挑战。因为离子注入形成的类高斯分布剖面，在其峰值（即注入原子的平均投影射程）附近通常具有相当陡峭的边缘。与扩散掺杂相比，离子注入常用于实现器件按比例缩小所需的更陡峭掺杂过渡，或形成低阻欧姆接触。因此，剖面边缘的陡峭程度很容易在一个德拜长度的尺度内发生剧烈变化，尤其是在低注入剂量的情况下。

上述Ziegler的修正算法不适用于小于两个德拜长度的深度范围，但在更深处，该算法能平滑地过渡到标准耗尽近似。许多离子注入剖面的投影射程远大于几个德拜长度，这时需要不同的处理方式。

类似的问题也出现在变容二极管等器件的高-低或低-高同类型掺杂过渡区的剖析中。在所有这些情况下，尤其是在掺杂梯度最陡峭的区域，局部电中性假设都不再成立。图6以一个类高斯分布的注入剖面 N_D(x) 为例解释了这种典型情况。移动载流子浓度 n(x) 由于扩散效应和排斥电场力的共同作用，会偏离掺杂剂的分布：在峰值处，自由载流子浓度偏低；而在剖面边缘，移动载流子则会形成比实际掺杂更长的“拖尾”。

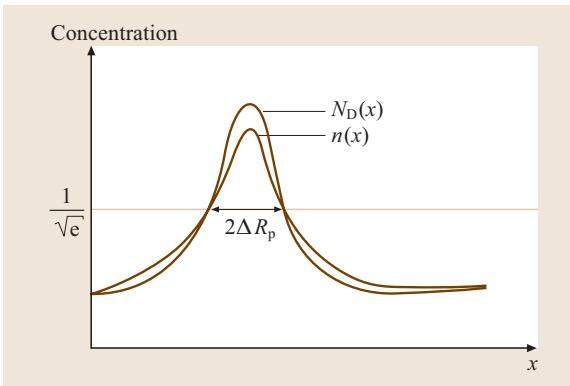
图6 注入掺杂剂剖面 N_D(x) 与自由载流子浓度剖面 n(x) 的对比：峰值附近 N_D(x) > n(x)，远离峰值处 n(x) > N_D(x)

将C-V测量结果与二次离子质谱 (SIMS) 测量的注入剖面进行比较可以证实这一点。C-V技术基于移动载流子的信号 (C = dQ/dV)，因此其得到的表观掺杂剖面缺乏真实剖面的陡峭性。然而，SIMS也无法取代C-V评估，因为它只能测量原子浓度，无法提供对器件功能至关重要的电学激活浓度信息。因此，必须改进C-V评估方法。

Kennedy等人为此做出了重要改进。他们开发了一种修正算法，通过求解同时考虑了多数载流子电荷贡献的泊松方程（忽略肖特基或pn结的反向电流），从移动载流子剖面 n(x) 中“提取”出真实的掺杂剖面 N(x)：

$$ N(x) = n(x) - /frac{/epsilon_0/epsilon_pkT}{q^2}/frac{/mathrm{d}}{/mathrm{d}x}/left(/frac{1}{n(x)}/frac{/mathrm{d}n(x)}{/mathrm{d}x}/right) /tag{4} $$

这里的 n(x) 是通过标准耗尽近似公式 (2)、(3) 从C-V测量中得到的。这个提取过程的前提是真实的移动载流子剖面已知。不幸的是，由于空间电荷边缘在约两个德拜长度范围内的弥散，C-V测量本身只能提供真实移动载流子剖面的一个近似。因此，Kennedy修正是获取更真实注入剖面形状的有效改进，但原则上，它仍无法完全消除德拜长度带来的物理限制。

对于离子注入剖面，一个有用的经验法则是：为使德拜长度畸变的影响足够小（误差<1%），注入剖面的半高宽 ΔR_p 应满足 ΔR_p ≥ 10L_D，其中 L_D 是给定掺杂浓度下的德拜长度。这意味着，在实践中，高剂量注入的剖面受德拜长度畸变的影响要小得多。

在应用公式 (4) 改进阶跃型高-低掺杂剖面时，如果条件允许，建议从高掺杂一侧开始耗尽。因为测量开始时德拜长度较短，有助于提高剖面重构的准确性。获取精确的掺杂浓度剖面，尤其是在面对复杂结构和陡峭梯度时，对测试技术和数据解读能力提出了很高要求。这正是专业检测实验室的核心价值所在。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测半导体电学性能，可靠准确。欢迎沟通交流，电话19939716636

电子和空穴的有效质量

半导体中移动载流子的有效质量，反映了其能带结构在 E(k) 图中曲率的信息。有效质量是一个张量，其分量定义为：1/m_ij² ≡ (1/ħ²) ∂²E(k)/∂k_i∂k_j，其中 E 是能带能量，k_i 是与载流子动量 p = ħk 相关的波矢 (k = 2π/λ)，ħ 是约化普朗克常数。半导体的能带结构由基于电子在晶体中波动性的薛定谔方程描述。

有效质量可以通过回旋共振和角分辨光电子能谱 (ARPES) 等实验方法测量。例如，III-V族半导体因其较小的电子有效质量（约0.07倍电子静止质量），载流子能在短时间内获得高速度，从而赋予了电子电路极高的高速潜力。