线弹性理论基础：应力与应变的定义及本构关系

日期：2025-07-23 浏览：14

线弹性理论基础：应力与应变的定义及本构关系

线性弹性理论是整个固体力学和结构工程分析的基石。该理论的起点，便是对应力（Stress）和应变（Strain）这两个核心物理量的精确定义。应力描述了物体内部相互作用的机械力强度，而应变则量化了物体内部各点之间的相对位移。在线性弹性范畴内，应力与应变通过一系列被称为“弹性常数”的材料固有属性关联起来。要准确评估结构部件中的应力分布，首先必须精确测定这些弹性常数。

应力的概念与描述

当一个物体承受外部载荷时，其内部不同部分之间会产生相互作用的内力。这些内力的强度通常通过作用在某个假想截面上的单位面积力来描述。我们可以设想在材料内部切开一个极小的测试面，并用一组力来替代被切去一侧的材料，这组力需确保该测试面维持在切割前完全相同的位置。当这个测试面的面积趋近于零时，作用于其上的力之和与该面积的比值，便定义为该点在该截面上的应力大小。应力的方向由其作用力的方向决定，且不一定垂直于该截面。

根据定义，固体内部某一点的应力状态会随着所取截面的方位和位置变化而改变。通常，我们会将应力分解为垂直于截面（法向）和平行于截面（切向）的分量。平行于截面的应力分量被称为剪切应力。由于应力既依赖于截面的方位，又依赖于作用力的方向，因此我们使用带有两个下标的符号 σ_ij 来表示应力。第一个下标 i 表示截面的法线方向，第二个下标 j 表示力的方向。

在一个笛卡尔坐标系 (x₁, x₂, x₃) 中，考虑一个法线方向为 x₁ 轴的微小截面，该截面上存在三个应力分量：σ₁₁, σ₁₂ 和 σ₁₃。

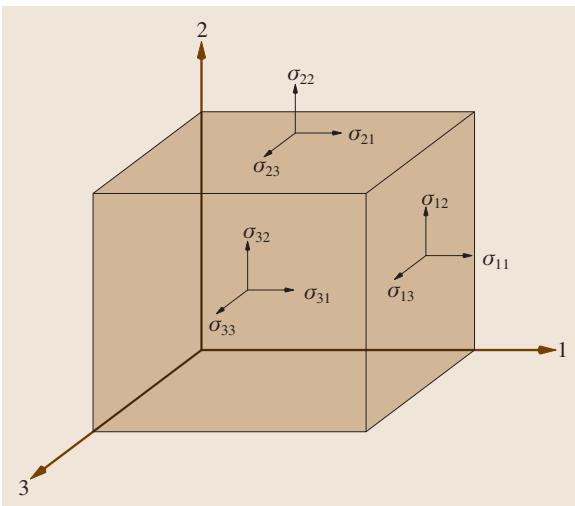σ₁₁：作用在 x₁ 面上，且力的方向平行于 x₁ 轴。这是一种法向应力，约定拉伸为正（拉应力），压缩为负（压应力）。
σ₁₂ 和 σ₁₃：均为剪切应力。σ₁₂ 作用在 x₁ 面上，力的方向指向 x₂ 轴；σ₁₃ 同样作用在 x₁ 面上，力的方向指向 x₃ 轴。

图1. 应力双下标表示法示意图。图中所有应力均为正值，位于立方体背面的应力方向与正面相反。

图1展示了一个微小立方体单元周围的应力分量。基于该立方体处于平衡状态的事实，可以推导出平衡方程。以 x₁ 方向为例，所有力的合力为零，可得：

$$ /frac{/partial/sigma_{11}}{/partial x_1} +/frac{/partial/sigma_{12}}{/partial x_2} +/frac{/partial/sigma_{13}}{/partial x_3} +F_1 = 0, /tag{7.1} $$

其中 F₁ 是沿 x₁ 方向的体力（如重力、电磁力等）。对于 x₂ 和 x₃ 方向，可以写出类似的平衡方程。

为了简化书写，人们发展出一种便捷的张量表示法。下标通常用 i, j, k 等小写字母表示，偏导数用逗号表示，重复出现的下标则表示对该下标遍历求和。于是，式(7.1)可以紧凑地表示为：

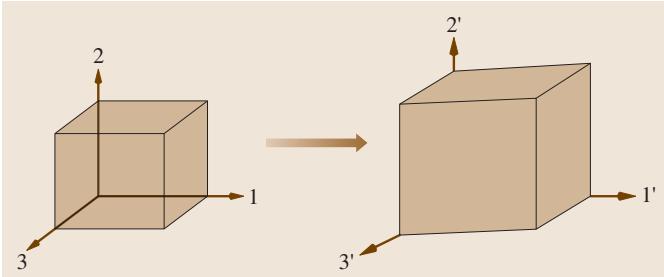图2. 变形后，立方体尺寸增加，棱边之间的夹角也不再是直角，这表明同时存在拉伸应变和剪切应变。

$$ /sigma_{ij,j} + F_i = 0. /tag{7.2} $$

将 i 分别取值为1, 2, 3，即可得到三个独立的平衡方程。体力 F_i 可以是常数，也可以是空间和时间的函数。

此外，通过分析图1中立方体的力矩平衡，可以证明应力张量是对称的，即 σ_ij = σ_ji。例如，对平行于 x₁ 轴的立方体棱边取力矩，可得 σ₂₃dx₂(dx₁dx₃) = σ₃₂dx₃(dx₂dx₁)，简化后即为 σ₂₃ = σ₃₂。同理可证其他分量也满足对称性。这意味着，在承受外力的物体内部，任意一点的9个应力分量中，只有6个是独立的。

应变的概念与描述

应变用于描述物体受力后内部各点之间的相对位移。想象物体内部一个原本是立方体的微元，在变形后变成了一个广义的六面体，其棱长可能不再相等，棱边之间的夹角也可能不再是直角（如图2所示）。

从这个变形的几何形态中，可以定义两种基本应变：

拉伸应变（正应变）：描述立方体棱长的变化。
剪切应变：描述立方体棱边之间夹角的变化。

若 u 代表物体内任意一点在 x₁ 方向的位移，那么在 x₁ 轴方向上与该点相距 dx₁ 的邻近点的位移为 u + (∂u / ∂x₁)dx₁。这两点在 x₁ 方向的相对位移量即为 ∂u / ∂x₁，它被定义为 x₁ 方向的拉伸应变，记作 ε₁₁。同理，若 v 和 w 分别是 x₂ 和 x₃ 方向的位移，则可以定义拉伸应变 ε₂₂ 和 ε₃₃。

剪切应变由立方体顶点处夹角的变化来定义。将立方体投影到 x₂-x₃ 平面（如图3所示），顶点夹角的变化量为 ∂v / ∂x₃ + ∂w / ∂x₂。工程上定义的剪切应变 ε₂₃ 为该角度变化的一半，即 ε₂₃ = (∂v / ∂x₃ + ∂w / ∂x₂) / 2。类似地，可以得到 ε₁₂ 和 ε₁₃ 的表达式。从剪切应变的定义可以看出，应变张量同样是对称的，即 ε_ij = ε_ji。

应力与应变都具有张量性质，这意味着当坐标系旋转时，它们的分量会遵循特定的张量变换法则。

应力-应变关系：本构方程

现在，我们来建立连接应力与应变的桥梁——本构方程。由于独立的应力分量和应变分量各有6个，最广义的线性关系可以用一个包含36个比例系数的方程组来表示：

$$ /sigma_{ij} = C_{ijkl}/epsilon_{kl}. /tag{7.4} $$

这里的系数 C_ijkl 被称为弹性刚度系数。根据约定，右侧重复出现的下标 kl 意味着对 k 和 l 从1到3进行求和。因此，对于左侧的每一个应力分量，右侧都有6项和6个对应的 C_ijkl 系数。

这36个弹性常数并非都相互独立。基于应变能的考虑可以证明，独立的常数最多只有21个。这个数字还会因为材料的对称性而进一步减少。对于立方晶系材料，独立弹性常数减少到3个。而对于各向同性（Isotropic）材料——即在所有方向上力学性能都相同的材料，独立弹性常数只有2个。

我们也可以将式(7.4)反写，用应力来表示应变，此时的连接系数 S_ijkl 被称为弹性柔度系数。刚度系数 C_ijkl 和柔度系数 S_ijkl 都是四阶张量，其数值依赖于坐标系的取向。

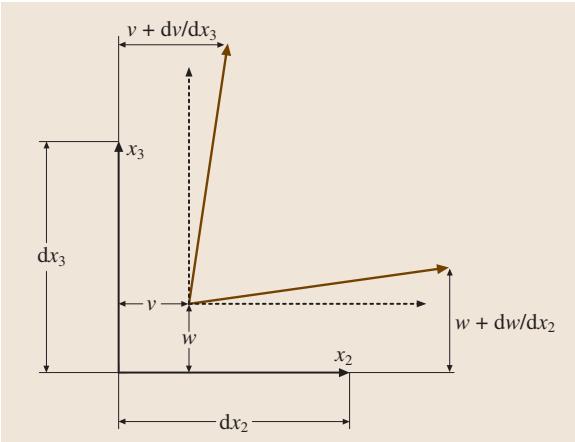图3. 从图中可以看出，x₂ 轴与变形后的 x₂’ 轴之间的夹角变化以及 x₃ 轴与 x₃’ 轴之间的夹角变化共同构成了剪切角。剪切应变 ε₂₃ = ε₃₂ 定义为该总角度变化的一半。

针对各向同性材料的实用关系式

由于大多数工程材料（如金属、部分陶瓷和聚合物）在宏观上可被视为各向同性，将上述普适性的张量方程转化为更具实际意义的形式至关重要。工程实践中最常用的弹性常数是：

杨氏模量 E：拉伸应力与拉伸应变之比。
剪切模量 μ (或 G)：剪切应力与剪切应变之比。
泊松比 ν：轴向拉伸时，横向应变与轴向应变之比的负值。

对于各向同性材料，这三个常数中只有两个是独立的，它们之间存在如下关系：

$$ /mu = /frac{E}{2(1 + /nu)}. /tag{7.6} $$

对于各向同性材料，应变可以用应力表示为：

$$ /epsilon_{ij} = /frac{1 + /nu}{E}/sigma_{ij} - /frac{/nu}{E}/delta_{ij}/Theta , /tag{7.7} $$

其中，δ_ij 是克罗内克符号（当 i = j 时为1，否则为0），Θ 等于 σ_ii，代表正应力之和 (σ₁₁ + σ₂₂ + σ₃₃)。展开式(7.7)可以得到6个关于应变分量的方程。

同样，应力也可以用应变来表示，此时使用剪切模量 μ 和拉梅常数 λ 更为方便：

$$ /sigma_{ij} = /lambda /epsilon_{kk}/cdot /delta_{ij} + 2/mu /epsilon_{ij}. /tag{7.8} $$

拉梅常数 λ 可以通过其他弹性常数表示：

$$ /lambda = /frac{E/nu}{(1 + /nu)(1 - 2/nu)}. /tag{7.9} $$

弹性常数的实验测定方法

在实际工程应用中，杨氏模量、剪切模量和泊松比是最常被测定和使用的参数，因此各类测试标准也主要围绕它们制定。

通常，测定弹性常数的实验构型是圆形或矩形截面的棒状或管状试样，在拉伸、弯曲或扭转载荷下进行测试。

静态测试：通过精确测量施加的载荷和试样的位移，再结合相应加载模式下的弹性力学解，可以计算出弹性模量。
动态测试：利用共振法或弹性脉冲在材料中的飞行时间来进行测量。

一般而言，动态技术获得的弹性模量结果比静态技术更为精确。两者之间的差异通常在-5%到+7%之间。这种差异可能源于多种效应的叠加，例如绝热与等温条件的区别、位错的弓出效应、其他非弹性行为以及两种方法本身精度和准确度的不同。准确测定这些参数对于材料研发、质量控制和结构设计至关重要。例如，要获得可靠的材料力学性能数据，对测试方法、试样制备、设备精度都有着极高的要求。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业提供材料弹性模量测试、材料力学性能检测等服务，结果可靠准确。欢迎沟通交流，电话19939716636

尽管世界各国采用不同的测试标准（如ASTM、ISO、GB等），但这些标准背后的物理原理和弹性力学方程是共通的。因此，只要遵循严谨的测试规程，不同标准下的测试结果在实验误差范围内应具有良好的一致性。

目前，用于测定材料弹性常数的五种通用测试方法包括：