失效分析深度解析：为何“足够强”的材料会发生致命脆断？

在现代工程领域，我们追求更高强度的材料和更宏伟的结构，但这却意外打开了“低应力脆断”这一潘多拉魔盒。工程师们时常面临一个令人困惑的悖论：一个根据传统强度理论计算绝对安全的零部件，却在远低于其设计极限的应力下，在某个寒冷的冬日突然断裂。这种突发性、灾难性的失效模式，是工业安全的一大隐患，也推动了失效分析从一门经验科学向一门精确定量科学的演进。

幽灵般的失效：当传统强度设计遭遇“低应力脆断”

低应力脆性断裂，如同一个潜伏的刺客，总在最意想不到的时刻给予致命一击。通过对大量此类失效案例的复盘，我们发现它们呈现出惊人的一致性：

1. “安全”的假象：断裂时的宏观应力水平极低，甚至在材料屈服强度的安全系数范围内。
2. 低温的“魔咒”：失效往往发生在较低的工作温度下，即所谓的“冷脆”现象。
3. 缺陷的“原罪”：断裂几乎总是始于结构中的应力集中区域，如尖锐的缺口、焊缝根部、或材料内部的夹杂物、微裂纹等。
4. 尺寸与速度的“帮凶”：厚大截面的结构和高加载速率（如冲击）会显著增加脆断的风险。

这些特征揭示了一个深刻的问题：传统的强度（如抗拉强度）和塑性（如延伸率）指标，虽然是材料选型的重要基石，但它们无法完整描绘材料在含有缺陷和特定工况下抵抗断裂的能力。我们需要一个全新的维度来衡量材料的“坚固性”。

超越强度：引入“韧性”——材料抵抗断裂的能量盾

为了解释为何有些材料“强而不韧”，材料科学家引入了“韧性”这一核心概念。韧性并非单一的性能，而是材料强度和塑性的综合体现。

韧性是什么？从应力-应变曲线看本质

韧性的物理意义是材料从开始受力变形直至最终断裂的整个过程中所能吸收的总能量。在应力-应变曲线上，这个能量值直观地表现为曲线下方的面积。

$$ U_{T} = /int /sigma /mathrm{d}/epsilon $$

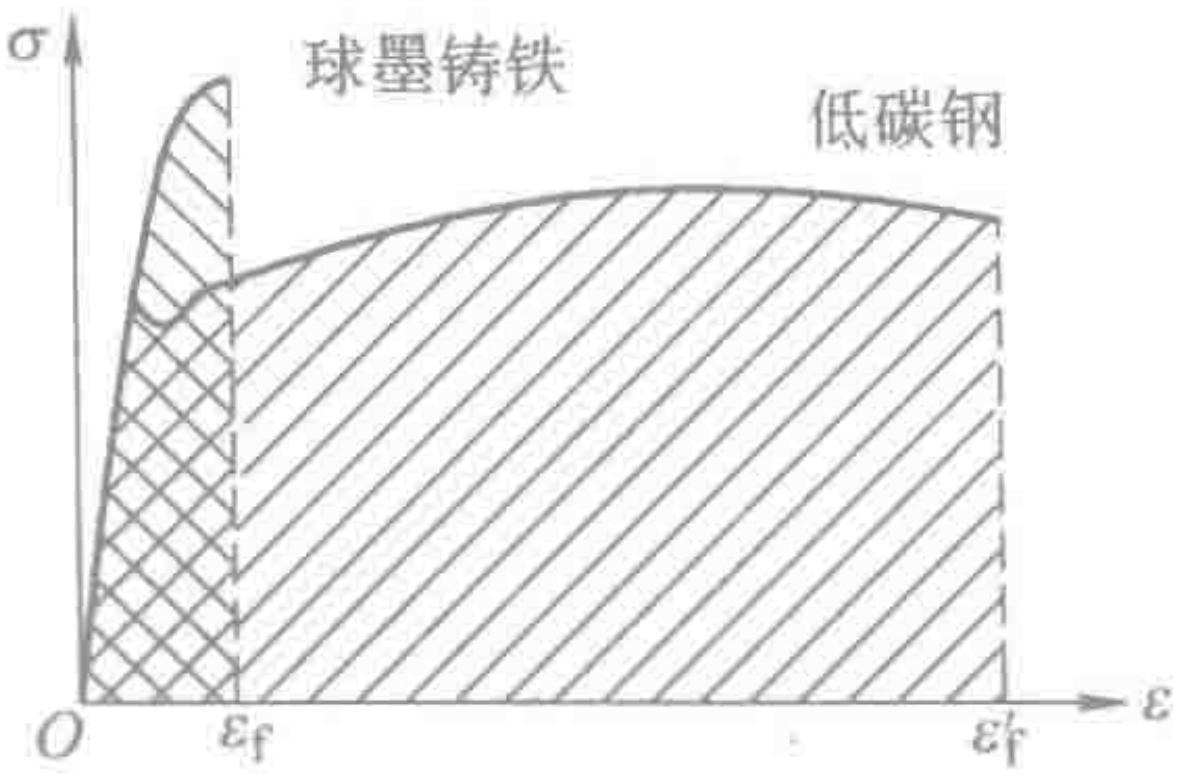
图1 低碳钢与球墨铸铁的应力-应变曲线对比

观察上图，一个经典的例子是低碳钢与球墨铸铁的对比。尽管球墨铸铁的抗拉强度更高，但其断裂前的塑性变形能力（延伸率）远逊于低碳钢。因此，低碳钢的应力-应变曲线所包围的面积要大得多，意味着其韧性远优于球墨铸铁。在受到意外冲击时，低碳钢能通过塑性变形吸收更多能量，从而避免灾难性的脆断。

实践中的标尺：夏比冲击试验的价值与局限

虽然通过积分计算韧性在理论上可行，但在工程实践中过于繁琐。因此，一种更简单、标准化的测试方法——缺口冲击试验（如夏比冲击试验）应运而生并沿用至今。

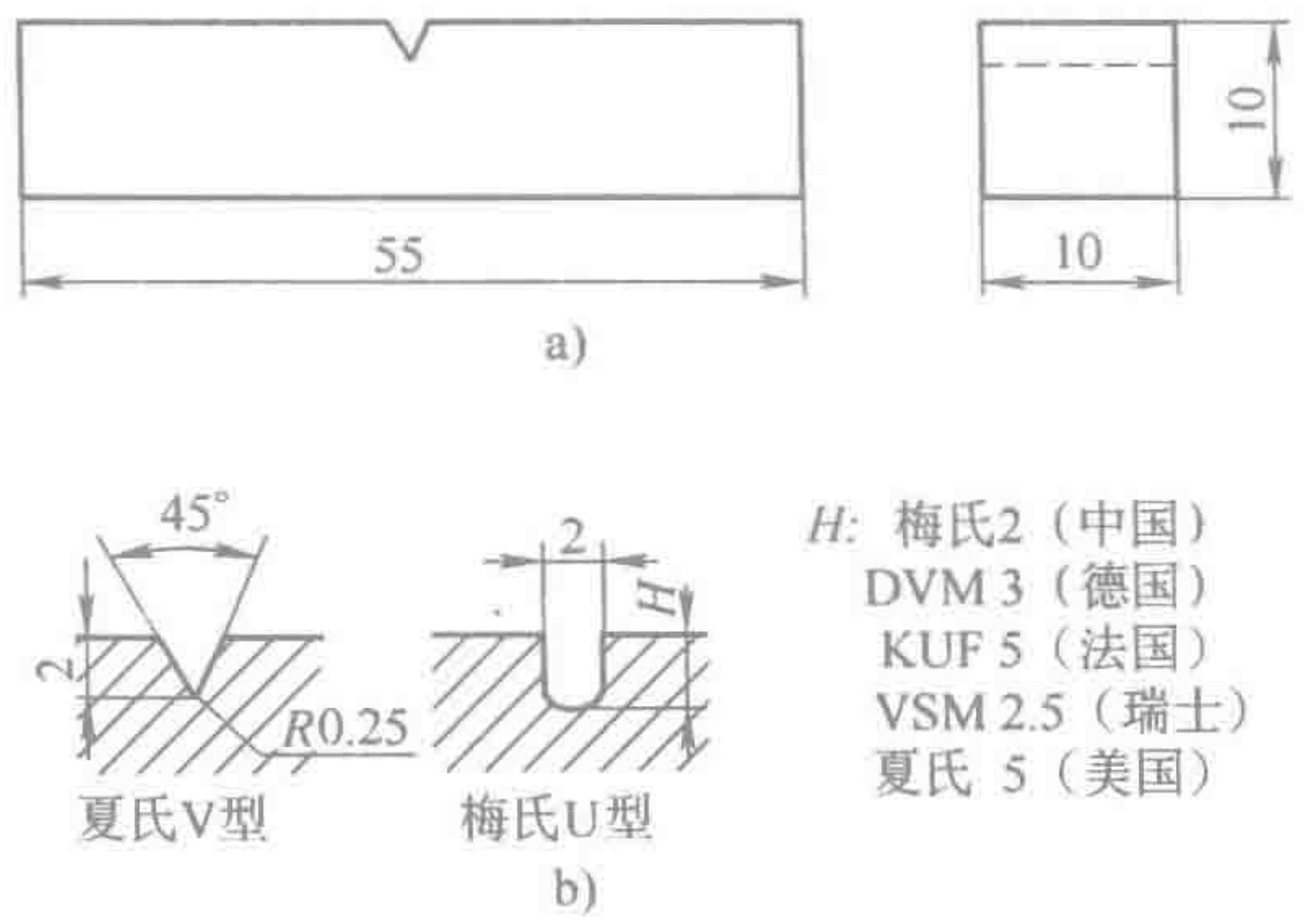
图2 标准化的夏比冲击试样

该试验通过一个摆锤冲击带有V型或U型缺口的标准化试样，测量试样断裂时所吸收的能量（冲击吸收功，记为KV或KU）。这个值能有效评价材料的韧性水平，以及热处理等工艺对韧性的影响。

更进一步，通过在不同温度下进行冲击试验，我们可以绘制出材料的冲击吸收功-温度曲线，并确定一个关键参数——韧脆转变温度（DBTT）。

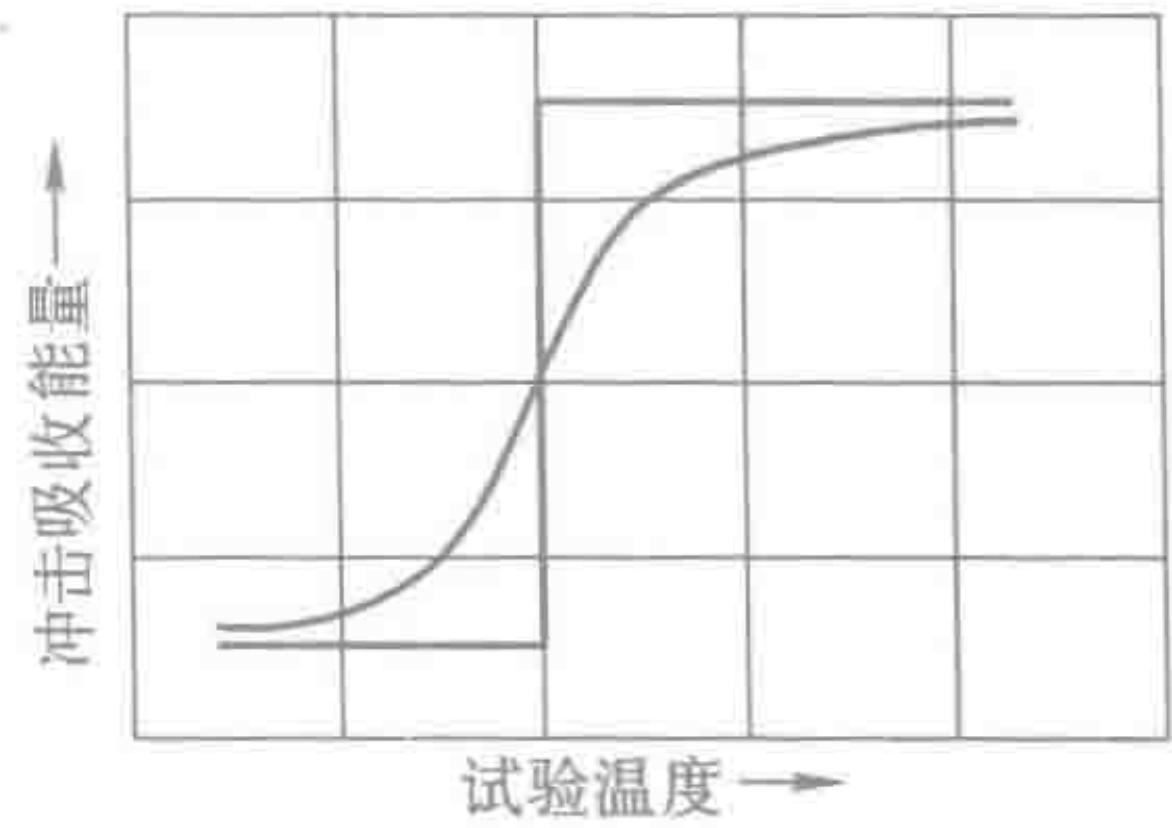
图3 材料的韧脆转变行为示意图

低于此温度，材料的韧性会发生悬崖式下跌，从韧性状态转变为脆性状态。因此，在设计选材时，必须确保设备最低工作温度远高于所选材料的韧脆转变温度。

然而，冲击功和韧脆转变温度本质上是“定性”或“半定量”的参考指标。它们能告诉我们材料A比材料B更韧，却无法直接代入设计公式，去计算一个含有特定尺寸裂纹的构件在多大载荷下会发生断裂。对于高风险、高要求的大型结构和高强度材料，这种模糊性是不可接受的。

从定性到定量：断裂力学在失效分析中的革命性突破

为了将韧性从一个相对比较的“参考值”转变为可用于精确计算的“设计参数”，20世纪中叶，断裂力学应运而生。它彻底改变了我们对结构安全的认知框架。

K_IC：为裂纹量身定制的“安全红线”

线弹性断裂力学（LEFM）的核心思想是：材料的断裂并非由名义应力决定，而是由裂纹尖端的应力场强度决定。为此，它引入了一个核心参量——应力强度因子 K_I。

$$ K_{/mathrm{I}} = Y /sigma /sqrt{a} $$

其中：

• σ 是作用在构件上的名义应力。
• a 是裂纹的特征尺寸（如裂纹长度的一半）。
• Y 是一个与裂纹形状、构件几何相关的无量纲因子。

K_I 精确地描述了裂纹尖端应力场的剧烈程度。相应地，每种材料都有一个内在的、抵抗裂纹扩展的极限能力，这个临界值被称为断裂韧度 K_IC。它和屈服强度一样，是材料固有的性能常数，单位通常为 MPa·m^1/2。

从理论到应用：如何用断裂韧度预测失效

有了断裂韧度 K_IC，安全设计的判据变得异常清晰和定量：

$$ K_{/mathrm{I}} = Y/sigma /sqrt{a} /leqslant K_{/mathrm{IC}} $$

这个公式的建立，是结构安全设计的一次飞跃。它意味着：

1. 容损设计成为可能：我们可以根据材料的K_IC值，计算出在给定工作应力下，构件所能容忍的最大裂纹尺寸。
2. 寿命预测得以实现：结合疲劳裂纹扩展理论，可以预测一个初始微小缺陷发展到临界尺寸所需的时间或循环次数。
3. 失效分析直指根源：当失效发生后，通过测量断口上的临界裂纹尺寸，可以反推出失效时的真实应力或材料的实际断裂韧度，为事故追责和后续改进提供定量依据。

随着技术发展，对于塑性较好的中低强度材料，弹塑性断裂力学（EPFM）进一步提出了J积分、裂纹尖端张开位移（COD）等更具普适性的韧性指标，使得断裂力学的应用范围更加广泛。

结论：选择正确的诊断工具，是预防灾难性失效的关键

从依赖传统强度设计，到引入韧性概念进行定性评估，再到运用断裂力学实施精确定量预测，我们对材料失效的理解在不断深化。这一认知升级的过程清晰地表明，面对复杂的工程失效问题，单一的测试或片面的认知是远远不够的。一次看似简单的脆性断裂，其背后可能交织着材料选择、加工工艺、服役环境和结构设计等多重因素。

当我们跳出单一的材料或工艺视角，从整个系统的应力状态、潜在缺陷和服役条件来审视一次断裂，根源才清晰地浮现。这种全局性的诊断思维，正是专业失效分析服务的核心价值所在——它提供的不是一份简单的测试数据，而是一个能够指导产品迭代和预防未来风险的根本性答案。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），专注提供一站式根本原因分析。央企背景，专家团队，助您快速定位产品失效的根本原因。欢迎垂询，电话19939716636