电热储能装置核心：耐火材料的热疲劳寿命分析

电网的平稳运行面临着一个长期存在的挑战：用电负荷的峰谷差。高峰期的电力紧张与低谷期的能源闲置，不仅影响供电稳定性，也推高了整体发电成本。为了实现电网的“削峰填谷”，工程师们开发了多种负荷平衡技术，其中，利用耐火材料构建电热储能装置，无疑是一种兼具经济性与可行性的技术路径。

该装置的核心思想是利用耐火材料优异的高热容特性。如下图所示，其基本结构并不复杂，主要由蓄热能力强的耐火制品（蓄能元件）构成核心，外壳则采用轻质耐火材料进行隔热保温。

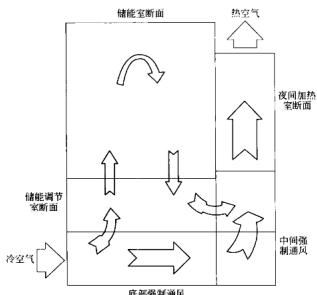
图1 电热储能装置简图

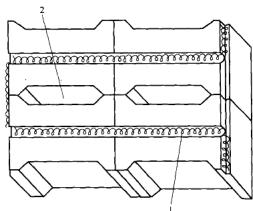
图2 电热储能用耐火材料蓄能元件（1—加热元件；2—空气通道）

其工作流程十分巧妙：在夜间用电低谷期，通过电阻加热系统将内部的蓄热砖（元件）加热至约800°C，将电能高效地转化为热能储存起来。当白天的用电高峰来临，送风系统启动，将冷空气送入装置内与高温蓄热砖进行热交换，再经过温度调节后，向用户供应稳定热风。这一过程有效转移了高峰时段的用电需求，起到了平抑电力负荷的功用。

对核心材料——耐火材料的性能拷问

要让这套装置稳定服役长达30年以上，经历数千次的充放热循环，对其核心部件——耐火蓄热砖的性能要求是极为苛刻的。

1. 高热容量：这是储能的基础。材料的比热容和体积密度共同决定了其单位体积的储热能力。
2. 高导热性：为了实现快速的能量储存与释放，材料必须具备良好的热量传导能力，确保热量能迅速遍布整个蓄热体。
3. 卓越的抗热震性与抗疲劳性：这是决定装置寿命的命脉。蓄热砖在每次循环中都经历着剧烈的升降温过程，这种反复的热冲击会诱发材料内部产生热应力，导致微裂纹的萌生与扩展，最终引发疲劳断裂。因此，材料必须具备极高的抗热震性能和长久的热疲劳寿命。

那么，如何从材料科学的角度，定量地分析并预测耐火材料在严苛循环工况下的服役寿命呢？答案藏在线弹性断裂力学之中。

基于断裂力学的热疲劳寿命预测模型

我们可以将电热储能装置中使用的耐火材料近似看作线弹性体。在线弹性断裂力学理论中，材料在疲劳载荷下，裂纹的扩展速率（da/dN，即每个载荷循环引起的裂纹亚临界扩展量）通常遵循以下关系式：

da/dN = A(Δk)ⁿ (式1)

这里，A 和 n 是与材料本身特性相关的常数，Δk 是交变应力强度因子，表征裂纹尖端应力场的强度，a 是裂纹长度，N 为循环次数。

应力强度因子 K 与施加的应力 σ 及裂纹的初始长度 a 直接相关：

K₁ = Yσa^1/2 (式2)

其中，Y 是一个与几何形状相关的常数。

当裂纹尖端的应力强度因子达到材料的断裂韧性极限值 K_IC 时，材料将发生瞬时断裂。

K_IC = Yσa^1/2 = (2Eγ_eff)^1/2 (式3)

式中，γ_eff 代表材料的有效表面能，E 为其弹性模量。

对于耐火材料这种非均质材料，我们通常使用基于断裂功 γ_eff 的概念，并将抗折强度 σ_f 代入，此时的临界应力强度因子记为 K_IR：

K_IR = Yσ_fa^1/2 = (αEγ_eff)^1/2 (式4)

基于上述理论，我们可以推导出评估和比较不同材料疲劳寿命的实用模型。对于形状相同的不同耐火材料，可以由式1推导出：

K_IR₁ⁿN₁ = K_IR₂ⁿN₂ = K_IR₃ⁿN₃ = ... (式5)

由此可得两种材料疲劳寿命 N 的比值关系：

N₁/N₂ = (K_IR₂/K_IR₁)ⁿ (式6)

假设两种耐火材料的初始裂纹状态和最终疲劳破坏程度相同，结合式4和式6，我们可以得到：

N₁/N₂ = (σ_f₂/σ_f₁)ⁿ (式7)

以及

N₁/N₂ = (E₂γ_eff₂/E₁γ_eff₁)^n/2 (式8)

式7和式8揭示了材料内在属性与其宏观疲劳寿命之间的深刻联系。式7表明，不同材料的疲劳寿命之比，与其抗折强度的反比的 n 次方成正比。简而言之，抗折强度越高的材料，其热疲劳寿命越长。而式8则从能量角度阐明，疲劳寿命与 Eγ_eff（弹性模量与有效表面能的乘积）这个组合参数直接相关。这些参数的精确测量对于材料的性能评估和筛选至关重要。

准确获取抗折强度、弹性模量、断裂功等关键力学性能参数，是进行可靠寿命预测和材料优化的前提。这正是专业检测实验室的核心价值所在。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测耐火材料热震稳定性、抗折强度、断裂韧性，可靠准确。欢迎沟通交流，电话19939716636

将理论与实际工况关联：热应力的影响

在电热储能装置中，引起疲劳的应力主要源于温度变化（ΔT）所导致的热应力。热应力 σ_f 可以表示为：

σ_f = αEΔT / ((1 - μ)C) (式9)

式中，α、E、μ 分别是耐火材料的热膨胀系数、弹性模量和泊松比，C 为形状因子。对于耐火材料，泊松比 μ 可近似取为 1/6。

将式9代入到式7中，我们便得到了一个更具工程指导意义的关系式，它直接将材料性能、操作工况与疲劳寿命联系起来：

N₁/N₂ = (α₂E₂ΔT₂ / α₁E₁ΔT₁)ⁿ (式10)

这个公式为我们进行材料选型和优化提供了清晰的理论指导。在选择用于电热储能的耐火材料时，应优先考虑热膨胀系数 α 和弹性模量 E 乘积较小的材料，因为这意味着在相同的温差下，其产生的热应力更低。

最后，我们来考察一个更简单但非常实用的情况：对于同一种耐火材料，在不同操作温差下的疲劳寿命关系。此时，材料参数（α、E）相同，式10可以简化为：

N₁/N₂ = (ΔT₂ / ΔT₁)ⁿ (式11)

该式明确指出，对于同一种材料，其疲劳寿命与工作循环的温差 ΔT 的 n 次方成反比。这意味着，即便是微小地降低循环温差，也能显著延长储能装置的使用寿命。这一结论不仅对材料研发，也对储能系统的运行策略优化具有重要的参考价值。