材料声衰减系数的脉冲反射法测量技术详解

声衰减，作为衡量声波在介质中传播时能量损失的关键物理量，是材料学、无损检测（NDT）和声学设计领域不可或缺的表征参数。它直接关联到材料的微观结构、内部缺陷及整体性能。然而，要精确测得材料的本征声衰减系数，并非简单地将探头对准试样读取数值。在实际测量中，我们得到的往往是“视在衰减值”，一个包含了多种物理效应与设备影响的复合结果。本文将深入探讨如何利用常规的A型脉冲反射式超声检测系统，通过水浸法精确测量纵波的声衰减，并解析如何从“视在值”中剥离干扰，逼近材料的“真实值”。

核心测量方法与前期准备

声衰减与频率密切相关，因此测量方法主要分为窄带脉冲反射法和宽带脉冲频谱法。此处，我们聚焦于应用更广泛、设备要求更通用的脉冲反射法。该方法利用非聚焦平面探头，在水浸条件下进行。

在启动测量前，一系列严谨的准备工作是保证数据可靠性的基石：

1. 探头声场特性评估：必须对所用的水浸平探头进行全面的声场标定，包括声束的指向性、对称性，以及关键的“距离-幅度”特性曲线。核心是精确测定其在水中的近场区长度（N）。
2. 仪器线性度校验：检查超声检测仪的垂直线性，并只在确认线性良好的区段内进行测量。通常，我们会选择仪器屏幕垂直刻度（如0-100%）中20%至80%的范围作为有效工作区。
3. 声程与对准：调整探头与试样间的距离（水程），确保试样底面处在探头的远场区，通常要求其位置大于等于3倍近场长度（≥ 3N）。同时，必须保证入射声束与试样上表面严格垂直，且试样的上、下表面保持高度平行。
4. 信号增益与显示调整：依据试样厚度，设定仪器的时间基线（扫查范围），并调整接收器增益，直至在屏幕上观察到一串清晰、稳定且幅度位于20%~80%线性区内的多次底面反射回波。

“视在衰减”的计算模型

完成上述准备后，即可通过分析多次底面回波的幅度变化来计算视在声衰减值 α (单位: dB/mm)。

基础计算公式：

$$ α = /frac{20/mathrm{lg}(A_m / A_n) - 20/mathrm{lg}(n / m)}{2(n - m)T} $$

其中：

• A_m, A_n：分别是第 m 次与第 n 次底面回波的幅度值 (n > m)。
• T：试样的厚度 (mm)。
• 20lg(n/m)：此项是一个关键的修正因子。它用于补偿理想活塞声源在传播过程中的声场扩散损失，这并非材料本身的吸收或散射所致。

在选择 m 和 n 时，应确保所选的回波信号未受到试样侧壁反射的干扰，并且两者之间有足够大的幅度差，以便于精确读数。进行多种材料的对比测量时，采用相同的 m 和 n 值是确保可比性的重要前提。

利用带刻度衰减器的方法：

若仪器配备了精确的带刻度衰减器，操作可以更为简便且能规避对接收器线性的依赖。具体做法是，分别将第 m 次和第 n 次底面回波的幅度用衰减器精确调节至同一基准高度（例如屏幕满幅的80%），并记录两次调节所需的衰减量差值 ΔdB。此时，计算公式简化为：

$$ α = /frac{Δ/mathrm{dB} - 20/mathrm{lg}(n / m)}{2(n - m)T} $$

全水浸条件下的修正：

当试样底部也浸没于水中（全水浸模式），声波在试样/水界面会发生反射和透射，导致能量并非100%返回。这种反射损失必须在计算中予以扣除。此时，视在衰减的表达式调整为：

$$ α = /frac{20/mathrm{lg}(A_m / A_n) - 20/mathrm{lg}(n / m) - δ}{2(n - m)T} $$

其中，反射损失 δ (dB) 的计算涉及水和试样的声阻抗：

$$ δ = /left[2(n - m) - 1/right]20/mathrm{lg}/left|/frac{z_{/mathrm{水}} - z_{/mathrm{试}}}{z_{/mathrm{水}} + z_{/mathrm{试}}}/right| $$

这里的 z_水 和 z_试 分别代表水和试样的声阻抗。

应对挑战：利用对比试块修正复杂系统误差

在某些情况下，由于试样厚度过小或设备限制，可能无法满足试样底面处于 ≥ 3N 远场区的理想条件。这时，引入对比试块法是一种行之有效的解决方案。

此方法的核心是利用一个已知（且极低）衰减特性的参照物来标定整个测量系统（包括声束扩散和界面反射）的固有损失。理想的对比试块材料，如经过特定热处理（淬火至马氏体再回火）的铬镍钼钢，其在10MHz下的纵波衰减系数可低至 2dB/m，几乎可以视为零。

测量流程如下：

1. 将厚度与被测试样相近的对比试块置于 ≥ N 的位置。

2. 用衰减器精确测量对比试块的一系列底面回波（B₁, B₂, …）的相对幅值，并绘制出“回波幅值 vs. 传播距离（2T × 次数）”的关系图。这条曲线（如下图上方所示）主要反映了由声束扩散和界面反射共同造成的系统性损失。

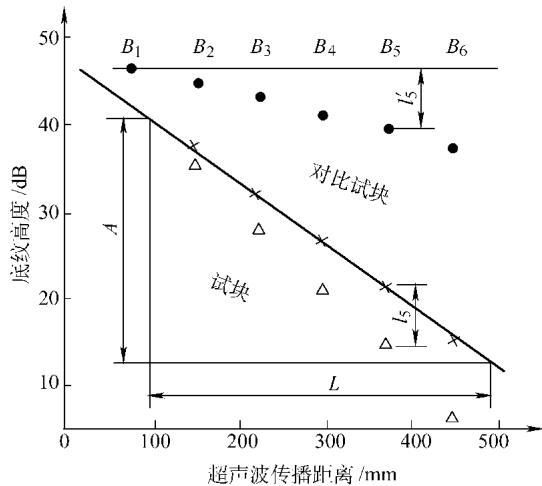   图1 用平板对比试块测定试样的衰减系数

3. 保持所有仪器参数不变，用被测试样替换对比试块，在相同位置测量其各次底回波的相对幅度，并绘制在同一张图上。

4. 通过对比两条曲线的差异，可以有效剥离系统损失，得到仅由试样自身引起的衰减。被测试样的声衰减系数 α 可由下式得出：

   $$ α = /frac{A}{L} $$

   其中 A 是由试样引起的净衰减量(dB)，L 是对应的声程(mm)。例如，根据图1中的示例数据，试样在400mm声程上产生了28dB的净衰减，则 α = 28dB / 400mm = 70dB/m。若测量频率为10MHz，再叠加上对比试块自身的真实衰减（2dB/m），可得试样在该频率下的真实衰减系数约为 72dB/m。

获取精确的材料性能数据，尤其是在面对非理想测量条件时，需要深厚的理论知识和丰富的实践经验。这正是专业检测实验室的核心价值所在。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测材料声衰减系数，可靠准确。欢迎沟通交流，电话19939716636

数据的表达与溯源：从奈培到分贝

从物理学角度看，平面简谐波的声压衰减遵循指数规律：

$$ p = p_0/mathrm{e}^{-/alpha_0x} $$

式中，p₀ 和 p 分别是初始声压和传播 x 距离后的声压，而 α₀ 则是介质的真实声衰减系数，其单位为奈培/毫米 (Np/mm)。

然而在工程应用中，为了便于测量和使用对数标尺，我们更常用分贝 (dB) 来表征衰减。两者之间的换算关系为：

α (dB/mm) = 8.69 × α₀ (Np/mm)

因为 1 Np ≈ 8.69 dB。

最后，一份专业、可信的衰减值报告，其价值不仅在于数字本身，更在于其完整的可追溯性。在给出任何“视在衰减值”时，必须附上详尽的测试条件说明，这包括但不限于：

• 仪器信息：制造商、型号、序列号，以及增益、发射脉冲参数等关键设置。
• 探头信息：制造商、型号、序列号、标称频率、晶片尺寸。
• 试样信息：尺寸、表面状态。
• 测量参数：用于计算的回波序号 (m, n) 及其幅度值，水程长度，以及是否进行了损失修正及其方法。

只有提供了完整的背景信息，测量结果才具有真正的可比性和科学价值。