超声横波检测技术深度解析：从SV波原理到SH波应用

在宏观缺陷的无损检测领域，横波检测因其独特的传播特性而占据着不可或缺的地位。其核心方法是利用透声斜楔，使纵波以特定角度斜射入试件与介质的界面，通过波形转换激发在试件中传播的折射横波（SV波）。这种方法通常被称为“斜角检测”，而使用的探头也因此得名“斜探头”。

要获得纯净、单一的横波波型，对入射角的控制至关重要。纵波的入射角必须精确地落在第一临界角与第二临界角之间。以钢材为例，实用的折射角范围通常在38°至80°之间。然而，实际检测环境远比理论复杂。材料内部的非均质性、探头换能器直径以及折射角度的改变，都可能诱发其他模式的波，例如在特定条件下会在试件表面出现瑞利波。因此，在横波检测的整个流程中，准确鉴别与分析声波的实际传播模式，是保证检测结果可靠性的基石。

一、 SV横波声场特性：斜探头的“隐形”挑战

当斜探头中的压电晶片（圆形或矩形）激发的纵波穿过斜楔，在试件界面发生折射，便形成了用于检测的横波声场。与纵波声场相似，横波声场中同样存在因波的干涉而产生的近场区，该区域内声压分布极不均匀，存在剧烈的极大与极小值波动。为了精确评估缺陷，理解横波声场的实际分布就变得尤为关键。

1. 近场影响区长度的计算

分析试件内的横波声场时，一个巧妙的思路是将实际的纵波声源等效为一个“虚拟横波声源”。我们假想这个声源位于试件材料内部，其轴线与折射横波的声束轴线完全重合，发射的声束也完全在被检测材料中传播，如图1所示。

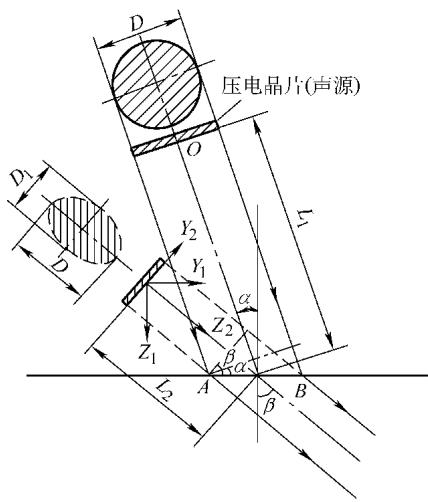
图1 斜探头横波声场的虚拟源分析

从几何投影关系不难看出，这个直径为 D 的实际圆形声源，其虚拟横波源是一个椭圆，长轴为 D，短轴为 D₁ = D(cosβ/cosα)。基于此模型，我们可以近似计算出该虚拟横波源在试件材料中的近场长度 N_t：

N_t ≈ (D² / 4λ₁₂) ⋅ (cosβ / cosα)

这里的 λ₁₂ 是指横波在试件中的波长。然而，这并非最终的近场长度。我们还必须考虑声波在斜楔中走过的那段声程 L₁。需要将这段声程折算成在钢中等效的横波声程 L₂：

L₂ = L₁ ⋅ (tanα / tanβ)

最终，在试件中实际的横波近场影响区长度 N’_t，就是虚拟声源的近场长度减去这段折算的声程：

N’_t = N_t - L₂

在进行缺陷定量评估时，通常要求检测区域位于近场影响区之外，以避开声压剧烈波动的区域。

2. 声束的指向性

声束的指向性描述了声能的空间分布特性，它直接影响着检测的覆盖范围和分辨率。

在 XZ₂ 平面（入射面）内，声束相对于轴线是对称的。横波主声束的指向角 θ₀ 可以通过以下公式计算：

• 对于直径为 D 的圆形晶片：θ₀ = arcsin(1.22 ⋅ λ₁₂ / D)
• 对于边长为 l 的方形晶片：θ₀ = arcsin(λ₁₂ / l)

然而，在 Y₁Z₁ 平面（垂直于入射面）内，声束的对称性被打破，如图2所示。其主声束的两个指向角 θ₁ 和 θ₂ 需要通过更复杂的公式来确定。

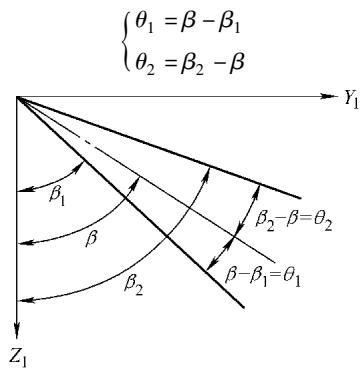
图2 Y₁Z₁ 平面内的声束指向角

• 对于直径为 D 的圆形晶片： sinβ₁ = sinβ ⋅ √(1 - (1.22λ₁₁/D)²) - (1.22λ₁₁c₁₂ / Dc₁₁) ⋅ cosα sinβ₂ = sinβ ⋅ √(1 - (1.22λ₁₁/D)²) + (1.22λ₁₁c₁₂ / Dc₁₁) ⋅ cosα

• 对于边长为 l 的方形晶片： sinβ₁ = sinβ ⋅ √(1 - (λ₁₁/l)²) - (λ₁₁c₁₂ / lc₁₁) ⋅ cosα sinβ₂ = sinβ ⋅ √(1 - (λ₁₁/l)²) + (λ₁₁c₁₂ / lc₁₁) ⋅ cosα

公式中的 λ₁₁ 和 c₁₁ 分别代表纵波在斜楔中的波长和速度。这些计算揭示了斜探头声场的复杂性，也凸显了精确校准和理解探头特性的重要性。

二、 SV横波检测的基本工作方式与参数选择

1. 工作原理与常用术语

当一束平面横波(T)以倾斜角 α_t 入射到钢/空气这类平界面时，会产生反射纵波(L’)和反射横波(T’)。在 α’_t < 90° 的理想情况下，反射横波与入射横波角度相同（α’_t = α_t），且不存在声束位移。声波会在试件的上下表面间反复反射，形成 “W” 形的传播路径（如图3）。若途中遇到缺陷，部分声能会反射回探头，在仪器屏幕上形成缺陷回波(F)；若声波传播至试件的端角，则会形成端角波(A)。

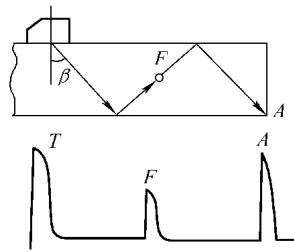
图3 横波检测示意图

为了标准化描述，行业内定义了一套常用术语（如图4）：

• 跨距 (Skip Distance)：声束轴线从入射点出发，经过一次底面反射后回到上表面的水平距离，称为“1次跨距”(Y_1S)。从入射点到第一次与底面相交点的水平距离则为“0.5次跨距”(Y_0.5S)。
• 波次：习惯上将 0 ~ Y_0.5S 路径上的声束称为一次波，Y_0.5S ~ Y_1S 路径上的称为二次波，以此类推。
• 缺陷位置：缺陷在探测面上的投影点到探头入射点的水平距离(l)和缺陷到探测面的垂直距离(d)是定位的两个关键参数。

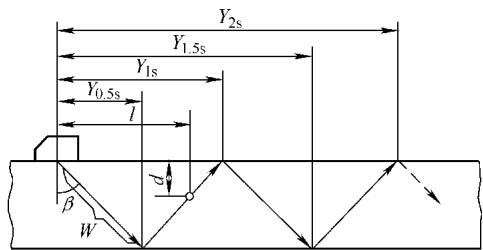
图4 横波检测中几个参量的示意图

2. 检测条件的优化选择

选择合适的检测条件是获取高质量信号的关键。

• 频率与性能：在同一材料中，横波的速度约为纵波的一半，这意味着在相同频率下，横波的波长更短。这带来了更好的指向性和分辨率，检测灵敏度也相应提高。但代价是声衰减更大，穿透能力有所下降。
• 波次与声程：为减少表面粗糙度带来的声能损失并简化信号分析，检测中通常优选一次波或二次波。同时，检测声程范围应尽量避开近场区（通常在 1N ~ 5N 之间，N为近场长度），以利于缺陷的准确评定，但也不能过远，否则衰减会过大。
• 探头角度：探头角度的选择需要根据试件厚度、所需波次和声程范围来权衡。对于薄件，为获得合适的声程并使用较少波次，应选择较大的折射角；反之，厚件则选用较小的折射角。一个通用的经验法则是：当检测截面厚度 ≥ 25mm 时，多采用 45°±2° 的折射角；当厚度 < 25mm 时，则倾向于使用 55°±2° 的折射角。

三、 检测前的准备与校准

严谨的准备工作是确保检测结果准确可靠的前提。

1. 斜探头性能测定

投入使用的每一个横波斜探头都应有唯一编号，并在使用前参照标准（如利用IIW试块）对其关键性能进行测量。这些性能必须符合相关技术文件的规定。例如，某些规范要求探头的实际频率与标称值的偏差在 2.25~10MHz 范围内不应大于10%，且实测值应标注在探头上。对于接触法使用的斜探头，若实测折射角与标称值相差超过2°，则必须修磨后方可使用。

表1总结了使用IIW试块对斜探头进行性能测量的常用方法。

表1 斜探头主要声学性能的测量方法（基于IIW试块）

2. 仪器校准与灵敏度调整

• 零点校正与范围调整：为了方便定位，必须扣除声波在斜楔中的传播时间，将探头入射点设为声程计算的零点。这一“零点校正”作业通常与检测范围的调整同步进行。以钢试件为例，可在IIW试块上，将入射点对准R100圆心，调整仪器使R100圆弧面的一、二次回波分别对准屏幕标尺的特定位置（如4和8格），即可完成校准。
• 距离-幅度曲线（DAC/AVG）的测绘：使用选定的仪器和探头组合，在带有标准人工反射体（如平底孔）的对比试块上，测绘出一条距离-幅度曲线。这条曲线反映了在整个检测范围内声压的分布情况。检测灵敏度通常依据此曲线进行调整，即在声压最低的距离处，将标准反射体的回波高度调节至规定水平。

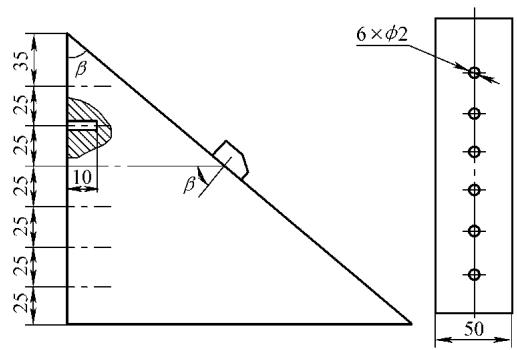
图5 用于测绘斜探头距离-幅度曲线的试块示例

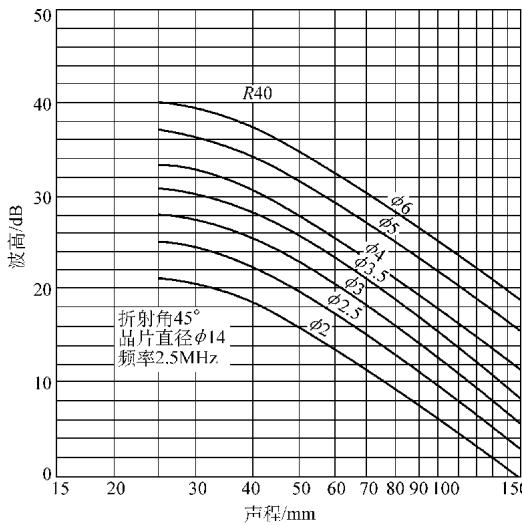
图6 实测斜探头AVG曲线示例

四、 缺陷的定位、定量与尺寸测量

1. 缺陷位置的确定

• 无背面反射位移的理想情况：如果已知试件厚度 t 和探头折射角 β，在测得从入射点到缺陷的声程 W 后，缺陷的水平距离 l 和深度 d 可通过简单的三角函数计算得出：

  • l = W⋅sinβ
  • 对于奇数次波 (n=1, 3, 5, …): d = W⋅cosβ - (n-1)t
  • 对于偶数次波 (n=2, 4, 6, …): d = n⋅t - W⋅cosβ

• 考虑背面反射位移的复杂情况：这是一个在实际检测中经常被忽略但又至关重要的物理现象。当横波在自由界面（如钢/空气）的入射角 α_t 大于某个临界值（对于钢，约为32.8°）时，尽管反射角等于入射角，但整个反射声束会沿界面平移一小段距离 Δ，即“声束位移”或“古斯-汉欣位移”。该位移量 Δ 的计算公式相当复杂。

  对于不同K值（K=tanβ）的探头，位移量也不同，如下表所示（以钢中 f=2.5MHz 为例）：

  表2 不同K值探头在钢中的声束位移估算

  探头K值	入射角 αt	Δ/mm
  0.8	38.66°	-2.5
  1.0	45°	0
  1.5	56.31°	1.0
  2.0	63.44°	2.0
  2.5	68.2°	3.0

  更复杂的是，声波在位移 Δ 的距离内是以非均匀平面波的形式传播，其传播速度也发生了变化，这使得精确的理论计算变得异常困难。在要求高精度定位的场合，最佳实践是利用与被检工件材质、厚度相同的专用对比试块进行校准，通过比较缺陷波与试块上已知位置反射体的信号来消除位移带来的误差。

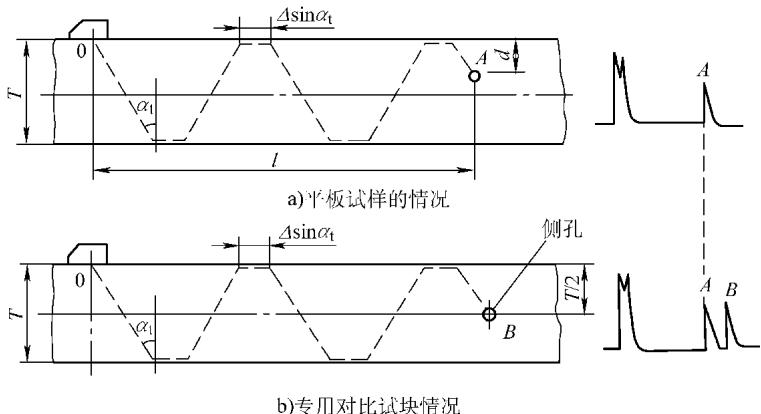
图7 考虑反射声束位移时利用对比试块进行缺陷定位的示意图

2. 缺陷的定量与长度测定

• 缺陷当量值：对于小缺陷，其定量方法与纵波检测类似，即将缺陷回波幅度与对比试块中相同埋深、已知尺寸的人工缺陷（如平底孔）的回波幅度进行比较，从而确定其“当量尺寸”。
• 缺陷长度测定：当缺陷的长度超过了声束在该处的截面宽度时，波高不再能反映其真实尺寸，此时需要对其长度进行估测。常用的方法有：
  • 最大波高衰减法（6dB法）：先找到缺陷回波的最高峰，然后将探头向左、右两个方向移动，直到波高分别下降到最大值的50%（即-6dB），记录此时探头移动的距离作为缺陷的指示长度。
  • 端点最大波高衰减法：对于长条形缺陷，可能存在两个端点反射的波峰。分别找到这两个端点波峰的最大值，再从各自位置向外移动，直到波高下降6dB，记录两个-6dB点之间探头中心线的距离作为指示长度。

不同的测长方法对同一缺陷可能得出差异很大的结果，具体检测时必须严格遵循相应标准或技术规程。这些复杂的评估过程，往往需要丰富的经验和对声学原理的深刻理解。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测无损检测、超声波探伤，可靠准确。欢迎沟通交流，电话19939716636

五、 特殊条件下的检测考量

1. 侧壁与角反射的影响

横波检测同样会遇到直角边和方角内反射的问题。图8展示了横波入射到直角边时的理论反射系数。在实际应用中，利用角反射时需注意，构成反射角的两个面尺寸都应远大于波长，否则反射条件不成立，这对于表面浅裂纹的检测尤其重要。

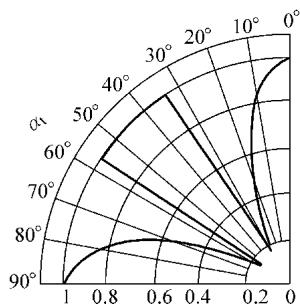
图8 钢中横波入射直角边的反射系数

从图中可以看出，当检测与表面垂直的较深裂纹时，采用与开裂面夹角为35°~55°的横波最为有利，而选用60°角则可能因反射系数低而不利于检出。

一个需要特别警惕的现象是：当使用折射角为60°的斜探头检测端角时（如图9），横波在端角平面的入射角为30°。在特定位置，探头可能接收到经波形转换后产生的反射纵波。由于纵波速度远大于横波，其回波信号会出现在正常的二次反射横波之前，极易造成误判。

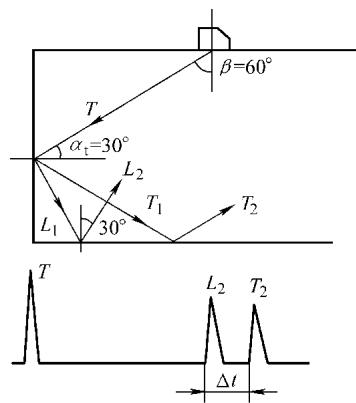
图9 60°横波在端角上因波形转换产生的纵波反射信号超前于二次横波反射的示意图

2. 缺陷高度的测量（TOFD与单探头技术）

• 衍射时差法（TOFD）：尽管TOFD技术通常采用纵波，但并无根本理由排斥横波。使用横波进行TOFD检测时，只需将计算公式中的纵波速度 c_l 替换为横波速度 c_t 即可。对于钢试件，采用横波TOFD时，较佳的折射角在50°至55°之间。
• 单探头技术：在无法部署双探头TOFD的情况下，可采用单探头技术估测缺陷高度。如图10所示，在探测到裂纹后，通过精确移动探头，分别找到裂纹上、下两个顶端衍射波的峰值位置，记录下各自的声程 W₁、W₂ 和探头水平位置 x₁、x₂。通过几何作图或专用公式即可计算出裂纹的垂直高度。为提高顶端衍射信号的识别能力和测量精度，可以考虑使用聚焦斜探头。

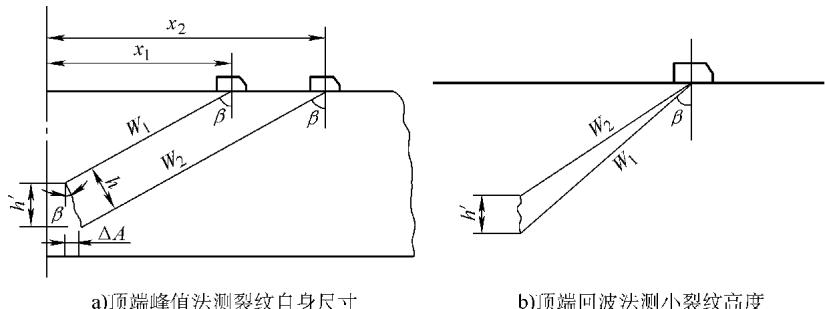
图10 利用单探头技术测量裂纹自身高度的示意图

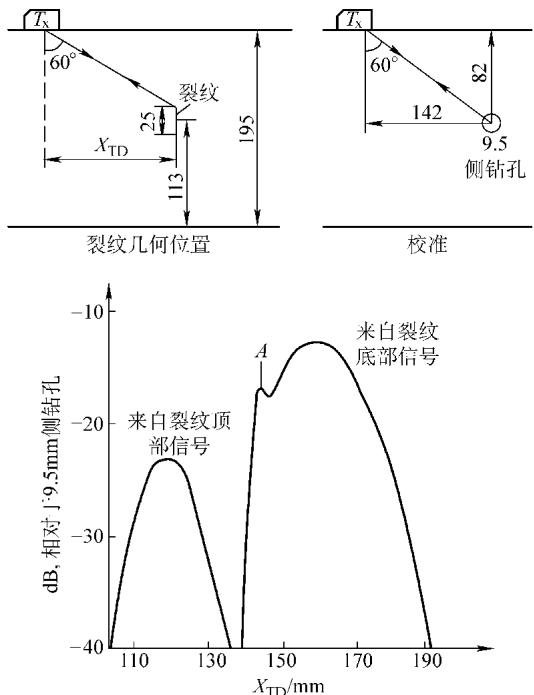
图11 2MHz、60°横波探头对一垂直条带裂纹的脉冲回波响应

3. 圆弧面试件的检测

当在曲率半径较小（如<500mm）的圆弧面上进行接触法检测时，为保证良好的声耦合，通常需要将探头斜楔的接触面修磨成与试件曲率相匹配的弧面。但这种修磨会改变探头的声学参数（如图12）：入射点位置、前后沿的入射角和折射角都会发生变化，甚至可能因为入射角范围过大而产生瑞利波或多余的纵波干扰。因此，经修磨后的斜探头，其特性必须重新进行全面的测量和标定。

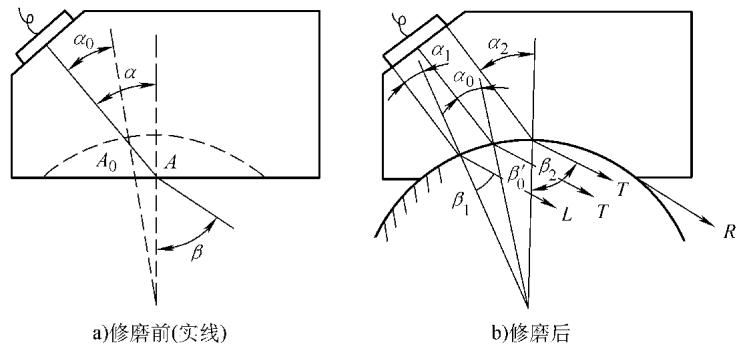
图12 斜探头为适应曲面而修磨后，声束分布发生的变化

六、 水平偏振横波（SH波）的独特应用

除了常见的SV波，还有一种特殊的横波——水平偏振横波（SH波），其质点振动方向平行于入射面。通过利用特定晶体（如Y切石英晶体或铌酸锂LiNbO₃）的横向压电效应，可以制作出垂直入射的SH波探头。

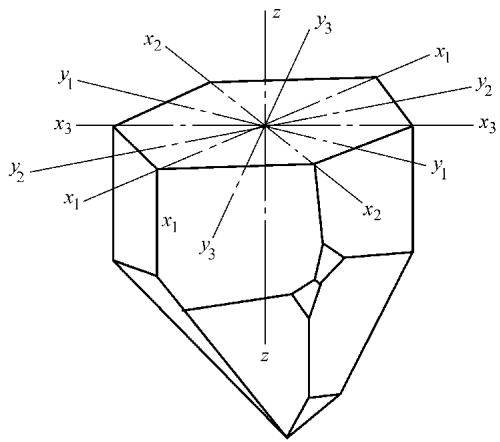
图13 石英晶体的晶轴方位示意图

SH波具有一些极为优越的特性：

• 无波形转换：无论是垂直入射还是斜入射，SH波在界面反射时只产生SH波，不会转换成其他波形，这使得信号分析大为简化。
• 特殊耦合剂：由于其水平偏振特性，常规的液体耦合剂效果不佳。传统上常使用蜂蜜，现在也已有专用的高粘度耦合剂。
• 各向异性检测：通过旋转探头来改变偏振方向，可以非常方便地检测出由材料结构（如晶粒取向）或应力导致的各向异性。
• 对垂直裂纹敏感：SH波的振动平行于试件表面，当遇到与表面垂直的裂纹时，能产生强烈的回波，检测灵敏度高。

综上，无论是常规的SV波还是特殊的SH波，横波检测技术都是一个内涵丰富、应用广泛的领域。掌握其核心原理，洞悉其在复杂条件下的行为，是每一位无损检测工程师提升技术水平的必经之路。