超声检测物理基础：波的传播、声场与衰减机制详解

要将超声波技术作为一种可靠的无损检测（NDT）工具，精准地探查材料内部的奥秘，其前提是必须深刻理解超声波自身的物理特性及其在介质中的传播规律。这不仅是理论探讨，更是确保检测结果准确性与可靠性的基石。

一、 振动与波：超声检测的物理语言

从本质上讲，超声波是机械振动在弹性介质中的传播过程，我们称之为弹性波或声波。这与电磁波（如光波、无线电波）在空间中的传播机理截然不同。声波的传播离不开介质，而频率（f）是描述其特性的核心参数。根据频率高低，我们将声波划分为三个区间：

• 次声波：f < 20 Hz
• 可闻声波：20 Hz < f < 20 kHz
• 超声波：f > 20 kHz

在无损检测领域，我们利用的正是人耳无法听见的高频超声波。

1. 连续波与脉冲波

在理论分析中，我们常会遇到连续波的概念，它指介质中各质点持续不断地振动。其中，所有质点以相同频率进行简谐振动的情形，构成了最简单的模型——简谐波。

然而，在实际的超声检测中，我们几乎总是使用脉冲波。这是一种持续时间极为有限的振动，以单个或间歇性的“波包”形式在介质中传播。傅里叶分析的数学原理告诉我们，任何非周期性的脉冲波，都可以被看作是无限多个、频率连续变化的简谐波的叠加。通过频谱分析仪，我们可以将时域中的脉冲信号分解，观察其在频域的构成，如下图所示。

图1：脉冲信号及其频谱分析。上图为时域脉冲信号（横坐标500ns/格），下图为其对应的频谱（横坐标5MHz/格）。

2. 丰富的波型

声源施加于介质的振动方向与波的传播方向之间的关系，决定了波的类型。在各向同性的固体材料中，最常见的波型是纵波和横波。当振动方向与传播方向平行时，是纵波；当振动方向与传播方向垂直时，是横波。

当波的传播受到介质边界（如板的表面）的约束时，还会产生导波，其中瑞利波（表面波）和兰姆波在特定检测场景中扮演着重要角色。它们与在材料内部自由传播的体波（纵波、横波）行为不同。此外，在各向异性材料（如复合材料、某些晶体）中，情况更为复杂，会出现振动方向与传播方向既不严格平行也不严格垂直的准纵波和准横波。

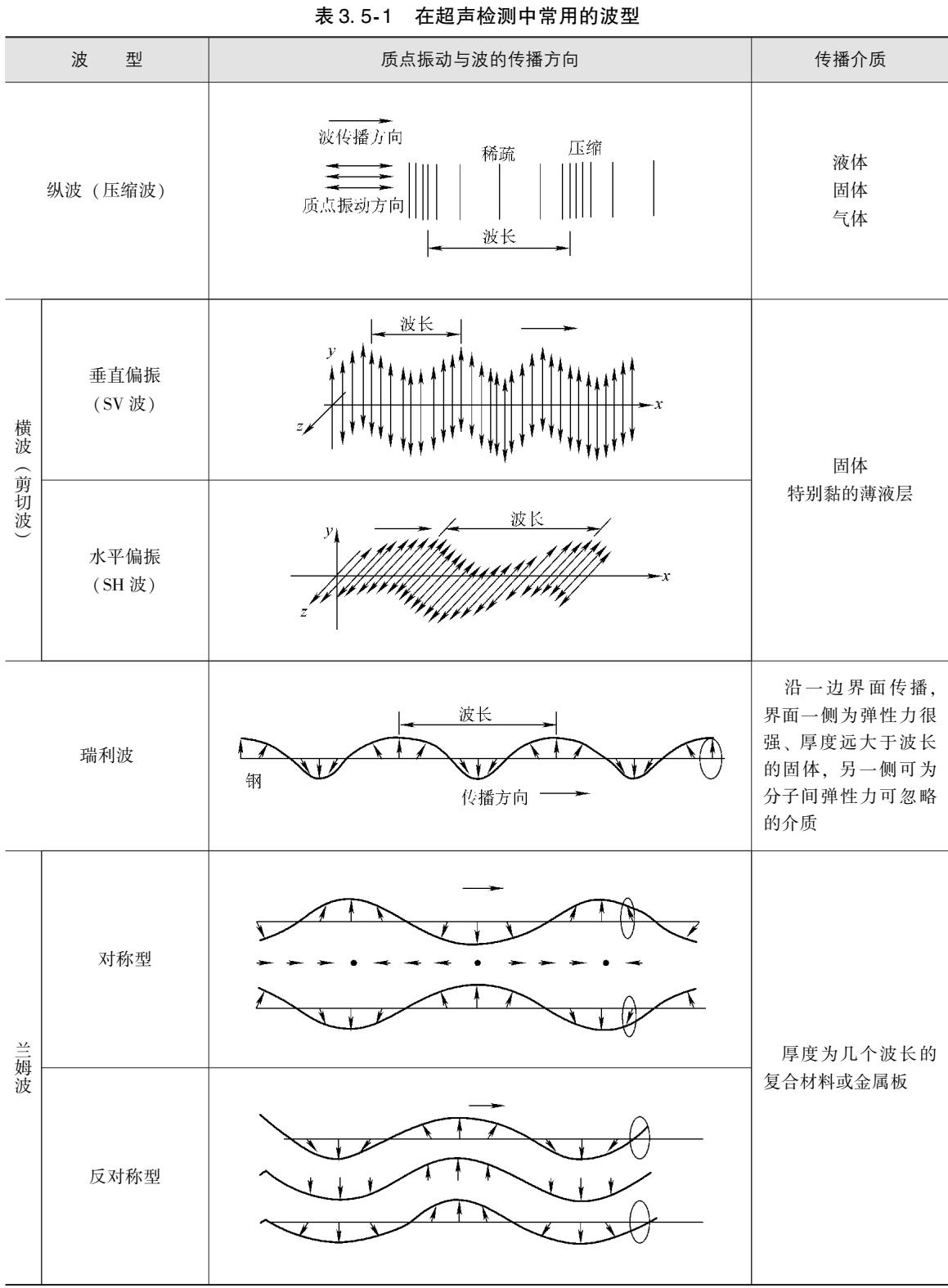
不同波型在介质中的传播速度由材料的弹性模量（E）、泊松比（σ）、密度（ρ）以及拉梅常数（λ, μ）等物理参数决定，具体关系见下表。

表1：不同波型在介质中的传播速度表达式

注：表中部分公式经过简化以适应通用显示。兰姆波的速度表达式相当复杂，此处不展开。

3. 波的形态：波阵面

在无限大的均匀介质中，波在某一瞬间到达的所有质点构成的几何面被称为波阵面。波阵面的形状决定了波的传播形式。

表2：波的传播形式及其特性

4. 几个核心声学参量

• 声压 (p)：有声波存在时，介质某点的瞬时压强与静态压强之差。
• 声强 (I)：单位时间内，通过垂直于声波传播方向的单位面积的声能量。它与声压的平方成正比：I = p² / (2ρc)。由于声强变化范围极大，工程上常用对数标尺——分贝 (dB) 来度量。
  • 分贝数 (dB) = 10lg(I₁ / I₂) = 20lg(p₁ / p₂)
• 声特性阻抗 (Z)：介质密度(ρ)与该介质中声速©的乘积，即 Z = ρc。它表征了介质阻碍质点振动的能力。声阻抗是决定声波在不同介质界面反射和透射行为的关键参数。

5. 散射与衍射

当超声波在传播途中遇到障碍物（如材料内部的夹杂、气孔等，其声阻抗与基体不同）时，会发生复杂的相互作用。

• 散射：若障碍物尺寸与波长相当或更小，波会以其为新波源向四周辐射，或发生不规则的反射和透射。这是检测微小缺陷的基础。
• 衍射：若障碍物尺寸远大于波长，波会绕过其边缘，进入其后的“几何阴影区”，路径发生弯曲。波长越长，衍射现象越明显。

在许多文献中，散射和衍射的概念有时会混用。但严格来说，衍射特指波绕过边缘的偏折行为，而散射则包含了这种偏折以及向原介质的回返（反射），其内涵更广。

二、 波在界面上的行为：反射、折射与波型转换

当超声波从一种介质传播到另一种声特性阻抗不同的介质界面时，其能量会重新分配，一部分被反射回原介质，另一部分则透射到第二种介质中。

1. 垂直入射

这是最简单的情形。声平面波从声阻抗为Z₁的介质垂直入射到声阻抗为Z₂的介质界面上。

• 声压反射系数 ®：反射波声压与入射波声压之比，r = (Z₂ - Z₁) / (Z₂ + Z₁)
• 声压透射系数 (t)：透射波声压与入射波声压之比，t = 2Z₂ / (Z₂ + Z₁)
• 往返透射比 (Tₚ)：衡量声波穿过界面、在第二介质中被全反射后再次穿过界面返回的效率，Tₚ = 4Z₁Z₂ / (Z₁ + Z₂)²

这些公式对于理解探头与工件间的耦合、以及缺陷的定量评估至关重要。例如，当声波从钢（Z大）入射到空气（Z极小）中，Z₂远小于Z₁，反射系数r约等于-1，意味着几乎所有能量都被反射，这正是利用内部缺陷（通常可视为含气界面）进行检测的原理。

当声波穿过一个中间薄层（如耦合剂层或覆盖层）时，其反射和透射行为会因薄层内的多次反射干涉而变得复杂，与薄层厚度及波长密切相关。

表3：大平面上声波垂直入射时的行为与表达式（简化）

2. 斜入射：现象更丰富

当超声波倾斜入射到界面时，情况变得有趣且复杂。除了反射和折射，还会发生波型转换。

图2：水/铝、水/钢界面往返透射比。图中显示了纵波入射后，透射纵波(E_ll)和透射横波(E_lt)的能量随入射角的变化，清晰展示了波型转换现象。

• 反射与折射定律：入射角、反射角、折射角与相应介质中的声速遵循斯涅尔定律（Snell’s Law）。
• 波型转换：当纵波斜入射到固-固或液-固界面时，除了产生反射纵波和折射纵波，通常还会同时产生反射横波和折射横波。这是因为入射波在界面处引起的质点振动可以分解为平行和垂直于界面的分量，从而激发不同模式的波。这一原理是超声斜探头检测焊缝等缺陷的基础。
• 临界角与全内反射：当声波从声速较低的介质（如水）入射到声速较高的介质（如钢）时，随着入射角的增大，折射角会先于入射角达到90°。此时的入射角称为临界角。
  • 第一临界角：折射纵波角度为90°时的入射角。超过此角度，纵波将不再进入第二介质。
  • 第二临界角：折射横波角度为90°时的入射角。超过此角度，横波也无法进入第二介质，发生全内反射。
  • 在全内反射条件下，虽然没有常规的折射波，但在第二介质表面下方极近的区域会产生一种沿界面滑行、振幅随深度指数衰减的非均匀平面波。利用第一临界角和第二临界角，可以分别在工件中仅激发沿表面传播的横波或表面波（瑞利波），实现特殊的检测应用。

图3：声束在界面上斜入射时的行为示意图

这些复杂的界面行为是超声检测技术多样性的根源，但也对检测工艺的制定和结果的判读提出了更高的要求。准确理解和计算各种系数及临界角，是优化探伤灵敏度和进行缺陷定量的关键。

三、 圆盘声源的声场：从理论到实践

实际超声检测中使用的探头，其核心是圆平面状的压电晶片，可近似为圆盘声源。它产生的活塞波声场分布，是所有检测工作的基础。

1. 声轴线上的声压分布：近场与远场

在不考虑衰减的理想情况下，圆盘声源轴线上的声压分布并非单调递减，而是呈现复杂的波动状态。

图4：圆盘声源声束轴线上的声压分布

这种波动现象将声场划分为两个截然不同的区域：

• 近场区 (菲涅尔区)：从探头表面到最后一个声压极大值点的区域。此区域内，声压因干涉效应而剧烈起伏，不适合进行缺陷的定量评估。近场长度N的估算公式为： N ≈ D² / (4λ) 其中，D是晶片直径，λ是波长。
• 远场区 (夫琅禾费区)：距离探头大于N的区域。此区域内，声压随着距离的增加而平稳下降，其行为类似于球面波，声场特性稳定，是进行缺陷定量分析的主要工作区。

2. 指向性与声束扩散

圆盘声源发射的声波能量并非均匀分布在所有方向，而是集中在以声轴为中心的一定锥角内，这种特性称为指向性。声场的主体能量束称为主瓣或主声束，旁边还分布着能量较弱的旁瓣。

图5：D/λ = 4 的圆盘声源指向性示意图，a为主声束，b为旁瓣。

在远场，主声束会以一个特定的角度（指向角或半扩散角 θ₀）向外扩散。其大小可由下式估算： θ₀ = arcsin(1.22λ / D)

这个公式揭示了一个核心关系：探头直径D越大，频率越高（波长λ越短），声束的指向性就越好，能量越集中，扩散角越小。 这也是为什么高频、大晶片探头常用于远距离或高分辨率检测的原因。

图6：圆盘声源 (D/λ = 16) 近场区不同截面上的声压分布

图7：圆盘声源 (D/λ = 16) 远场区不同截面上的声压分布

3. 脉冲波声场

实际使用的脉冲波声场，可以理解为由其频谱中各种频率成分的连续波声场叠加而成。实验表明，脉冲的持续时间（或振荡次数n）对声场有显著影响。

图8：圆盘声源脉冲声场的声压分布对比 (a: n=2, b: n=24)

短脉冲（如n=2，对应宽频带探头）的近场区声压波动远比长脉冲（如n=24，对应窄频带探头）来得简单，干涉点和旁瓣效应都大为减弱。这使得宽带探头在近表面检测和要求高轴向分辨率的场合更具优势。

四、 超声波的衰减：能量在传播中的损耗

声波在真实介质中传播时，其能量会随传播距离的增加而不断减小，这一现象称为衰减。衰减是影响检测灵敏度和探测深度的决定性因素。衰减主要由三部分构成：

1. 扩散衰减：也称几何衰减，是由于声束随距离扩展，能量散布到更大面积上导致的。它只与波的几何形状有关，与介质无关。远场的活塞波，其声压与距离x成反比。
2. 吸收衰减 (αₐ)：介质质点在振动过程中因黏滞性、热传导等内部摩擦效应，将声能转化为热能。吸收衰减与频率通常成正比关系 (αₐ = c₁f)。
3. 散射衰减 (αₛ)：在多晶材料中，声波遇到不同取向的晶粒界面时发生散射，导致声能偏离主传播方向。散射衰减与频率和晶粒尺寸的关系极为密切。当晶粒尺寸d远小于波长λ时，散射衰减系数与频率的四次方 (f⁴) 和晶粒尺寸的三次方 (d³) 成正比 (αₛ = c₂Fd³f⁴)。

总的衰减系数 α = αₐ + αₛ。因此，考虑了介质衰减和扩散衰减后，远场声压的表达式为： p = p₀ * (Aᴅ / (λx)) * e⁻ᵃˣ

这个关系清晰地表明，频率越高，衰减越快。这构成了超声检测中的一个基本矛盾：提高频率可以改善分辨率和指向性，但会牺牲探测深度。因此，选择合适的检测频率，是在分辨率和穿透能力之间进行的关键权衡。

获取精确可靠的衰减测量结果，对材料性能评估和缺陷定量至关重要。然而，衰减测量受到整个声学系统的深刻影响，包括驱动脉冲的频谱特性、探头的频率响应和阻尼情况等。不同系统间的测量结果可比性较差，即使是标称相同的系统，其再现性也通常在±15%左右。因此，要获得一张信噪比高、结果可靠的图谱，对样品制备、设备参数配置都有极高要求。这正是专业检测实验室的核心价值所在。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测无损检测，可靠准确。欢迎沟通交流，电话19939716636