X射线与γ射线检测物理学：从产生、相互作用到衰减

在无损检测（NDT）领域，我们常常需要借助“眼睛”无法企及的手段来洞察材料的内部结构。X射线与γ射线，这两种高能电磁波，正是我们赖以洞察微观世界、保障宏观工程质量的关键探针。要真正驾驭这些技术，我们必须回归其本源——理解它们的物理基础。

1. X射线的本质与特性

1895年，物理学家伦琴在探索阴极射线的过程中，偶然发现了一种全新的、具有极强穿透力的辐射，并将其命名为X射线。后续的研究揭示，X射线与可见光同属电磁波家族，但其能量与行为模式却大相径庭。

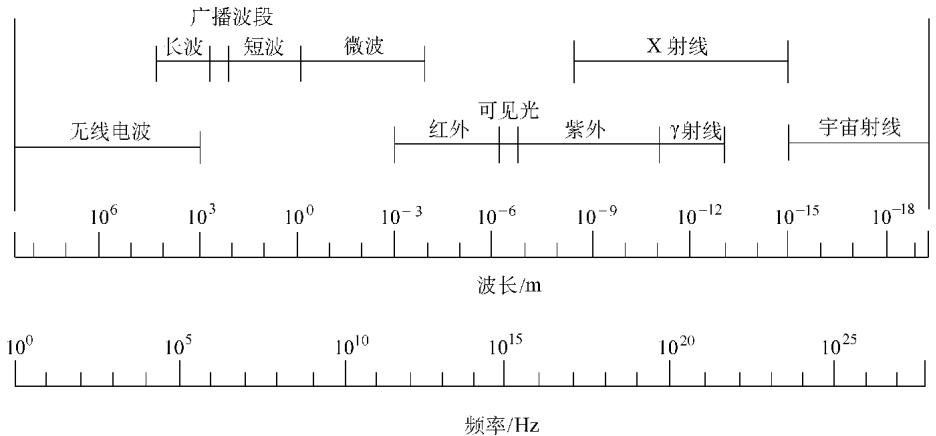
图1 电磁波谱

依据量子理论，X射线是由高能光子构成的粒子流。单个光子的能量 ε 可由普朗克公式描述：

ε = hν

其中，h 为普朗克常数（约为 6.626 × 10⁻³⁴ J·s），ν 为电磁波的频率（Hz）。这种能量层级赋予了X射线独特的波粒二象性，使其在检测应用中展现出多种关键性质：

• 中性与直线传播：在真空中，X射线以光速沿直线传播，其路径不受电场或磁场的影响，这保证了射线照相成像的几何准确性。
• 微弱的折射与反射：与可见光不同，X射线在穿越不同介质界面时，几乎不发生镜面反射，其折射率也无限接近于1。这意味着它能轻易“透视”物体，而非被表面弹开。
• 苛刻的干涉与衍射条件：由于X射线的波长极短，远小于可见光，只有在面对原子晶格、微孔或极细狭缝这类微观结构时，才能观察到显著的干涉与衍射现象。这正是X射线衍射（XRD）技术分析晶体结构的基础。
• 强大的穿透能力：人眼无法感知X射线，但它能穿透对可见光不透明的物体。根据能量不同，X射线可分为：
  • 硬X射线：波长短，光子能量高，穿透力强，适用于厚重工件的检测。
  • 软X射线：波长较长，光子能量低，穿透力弱，多用于薄壁材料或低密度材料的分析。
• 物理与化学效应：当X射线与物质相互作用时，会引发一系列效应，如使原子电离、激发某些材料产生荧光（XRF技术的基础）或诱发光化学反应。
• 生物效应：X射线携带的高能量能够破坏生物细胞和组织，这是其在医疗领域用于治疗的同时，也要求在工业应用中必须严格进行辐射防护的原因。

X射线谱：连续谱与特征谱的二重奏

在工业X射线管中，通过高电压加速的电子流高速撞击金属阳极靶，从而产生X射线。其辐射强度随波长的分布，即X射线谱，呈现出一种独特的结构，由“连续谱”和“特征谱”两部分叠加而成。

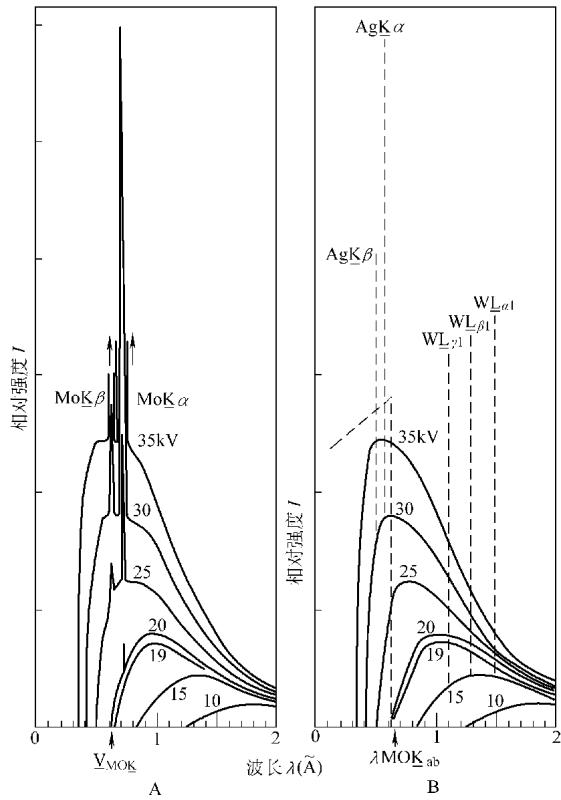
图2 钼靶的X射线谱

连续谱，也被称为韧致辐射（Bremsstrahlung），源于高速电子在靶原子核的电场作用下突然减速时损失的动能。这部分谱线呈现出平滑的、连续的能量分布。其总强度（I）与管电流（i）、管电压（V）以及阳极靶材的原子序数（Z）密切相关，经验关系式可近似为：

I = αiZVᵐ

式中，α 是一个比例常数，当电压单位为kV、电流单位为mA时，其值在 (1.1 - 1.4) × 10⁻⁶ 左右；指数 m 约等于2。这表明，提高管电压对射线强度的影响远大于提高管电流。

连续谱的辐射强度在空间分布上并非均匀。

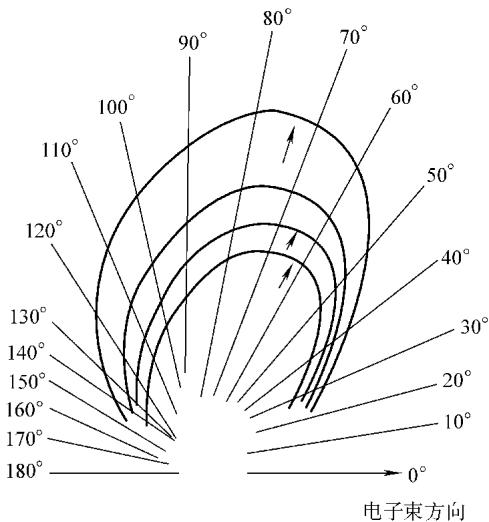
图3 连续谱X射线强度空间分布（注：曲线从里到外依次为：16.4keV，24.0keV，31.0keV，37.8keV）

根据能量守恒，电子的全部动能都转化为光子能量的极限情况，决定了连续谱存在一个最短波长（λ_min），它完全由加速电压（V）决定：

λ_min = (12.4 / V) × 10⁻⁸ (cm)

特征谱，则像是材料的“指纹”。当加速电压足够高，超过靶材原子的某一“激发电位”时，入射电子的能量足以将靶原子内层轨道的电子（如K层、L层）击出。外层电子会迅速跃迁填补这个空位，并以特征X射线的形式释放出能量差。由于原子能级是量子化的、不连续的，因此产生的X射线能量（波长）也是特定的，表现为在连续谱背景上叠加的若干根尖锐的谱线。

这些谱线根据电子跃迁的壳层被命名为K系、L系、M系等。每种元素的特征谱线结构都是独一无二的，其波长由原子序数（Z）决定，遵循莫塞莱定律：

√ν = C(Z - σ)

其中ν是特征谱线的频率，C和σ是常数。这一定律使得通过分析特征X射线来识别材料成分成为可能（X射线荧光分析，XRF）。

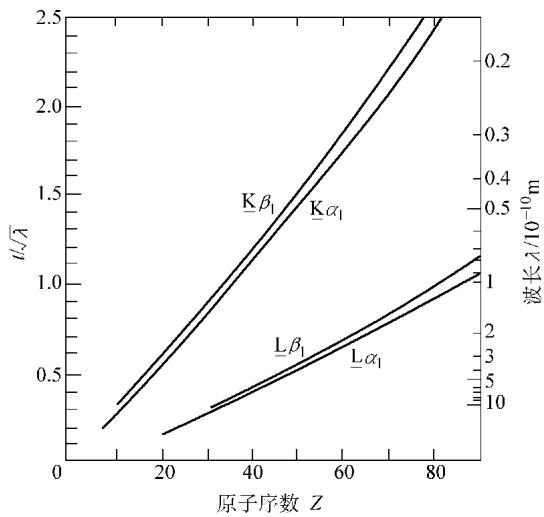
图4 莫塞莱定律示意图

下表列出了一些常见元素的K系激发电位与主要特征谱线波长。

表1 部分元素的激发电压与K系主要谱线波长

2. γ射线：源自原子核的辐射

与X射线源于核外电子跃迁不同，γ（伽马）射线是原子核内部能量变化的产物。1896年，贝克勒尔发现了天然放射性现象，即某些不稳定元素的原子核（核素）会自发地放出射线，转变为另一种核素，这一过程称为放射性衰变。

放射性衰变规律

放射性衰变是一个随机的统计过程。大量放射性原子核的衰变数量遵循指数衰减规律：

N = N₀e⁻ˡᵗ

式中，N₀ 是初始时刻（t=0）的原子核数量，N 是t时刻尚未衰变的原子核数量，λ 是衰变常数，表征单位时间内单个原子核的衰变概率。

在工程应用中，我们更常用“半衰期”（T_1/2）来描述衰变的快慢。它指放射性原子核数目衰减到初始值一半所需的时间。半衰期与衰变常数的关系为：

T_1/2 = 0.693 / λ

γ射线的产生与性质

在α衰变或β衰变后，新生成的子核往往处于不稳定的高能级激发态。当这些激发态的原子核向低能级或基态跃迁时，会以γ光子的形式辐射出多余的能量，这就是γ射线。

由于不同核素的能级结构是特定且分立的，因此每种放射源（如钴-60、铱-192）产生的γ射线都具有特定的、不连续的能量，即线状谱。

在本质上，γ射线与X射线一样，都是高能光子流，因此它们的主要物理性质，如穿透性、电离能力等，是相同的。主要区别在于来源——γ射线源自原子核，而常规X射线源自核外电子。

3. 光子与物质的相互作用：检测的物理核心

无论是X射线还是γ射线，其检测能力的根本，在于它们穿过物体时与物质发生的相互作用。这些相互作用导致射线能量和方向的改变，从而携带出物体内部的密度和成分信息。

光子与物质的相互作用对象主要包括原子中的电子、原子核以及它们周围的电场。根据能量交换方式，可分为吸收、弹性散射和非弹性散射。对于无损检测中常用的能量范围，以下四种效应占据主导地位。

表2 光子与物质相互作用的分类

注：表中 τ、σ、κ 为相应作用的吸收或散射系数，Z 为原子序数，hν 为光子能量。① 指主要相互作用，② 指次要相互作用。

光电效应 (Photoelectric Effect)

当入射光子的能量足以克服原子内层电子（如K层电子）的束缚能时，光子会将其全部能量传递给该电子，使之脱离原子成为自由的“光电子”，而光子自身则完全消失。

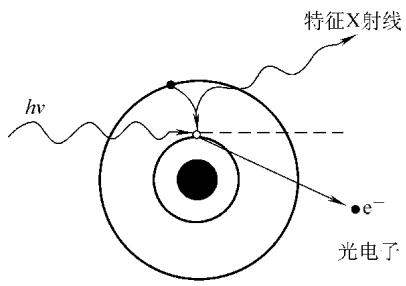
图5 光电效应示意图

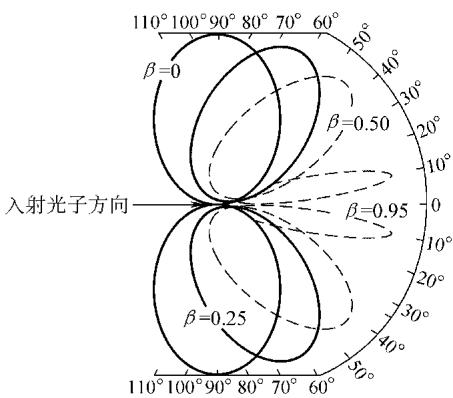
图6 光电效应中产生的光电子分布图

光电效应的发生概率（光电截面）与物质的原子序数Z的4-5次方成正比，并随光子能量的增加而急剧下降。这意味着，在低能量射线（软X射线）和高原子序数材料（如铅、钨）中，光电效应是主要的吸收机制。它对材料成分的差异极为敏感，是形成高对比度X射线图像的关键。

光电效应后，原子内层的空穴会被外层电子填充，这个过程会伴随着特征X射线（荧光辐射）或俄歇电子的发射。

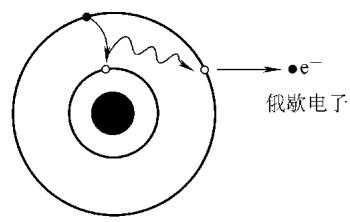
图7 俄歇效应示意图

康普顿效应 (Compton Scattering)

康普顿效应是入射光子与原子外层束缚较弱的电子或自由电子之间的“弹性碰撞”。

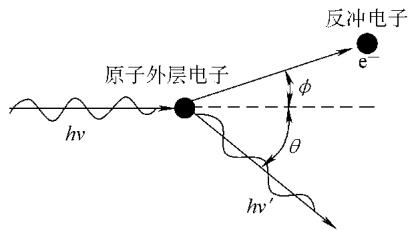
图8 康普顿效应示意图

在此过程中，入射光子将一部分能量转移给电子，使其成为“反冲电子”，而光子自身能量降低、波长变长，并改变了原来的传播方向，成为“散射光子”。

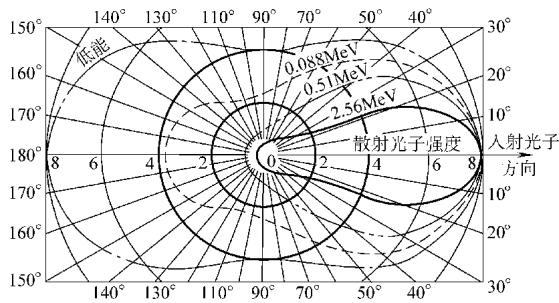
图9 康普ton散射中散射光子的角分布

散射后光子波长的增加量 Δλ 只与散射角 θ 有关：

Δλ = λ’ - λ = (h / m₀c)(1 - cosθ)

其中，常数 h/m₀c 被称为电子的康普顿波长 (λ₀ ≈ 2.426 × 10⁻¹² m)。

康普顿效应的发生概率与物质的原子序数Z成正比，也与电子密度有关。在中等能量范围（约0.1 MeV至10 MeV），对于大多数工程材料（如钢、铝），康普顿效应是主导的相互作用。它对材料密度的变化敏感，但由于散射线的存在，会降低图像的对比度和清晰度，是射线检测中需要重点控制的干扰因素。

电子对效应 (Pair Production)

当入射光子的能量超过一个阈值（1.02 MeV，即两个电子的静止质量能量之和）时，它在原子核的强电场附近可能直接转化为一个正电子和一个负电子，这个过程称为电子对效应。入射光子在此过程中消失。

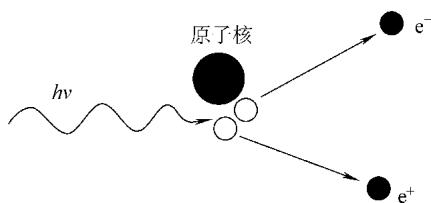
图10 电子对效应示意图

产生的正负电子对的总动能等于入射光子能量减去1.02 MeV。电子对效应的发生概率与原子序数Z的平方成正比，并随能量的升高而增加。因此，在高能量（>10 MeV）和重元素中，电子对效应成为主要的吸收方式。这在超厚工件的高能射线检测中非常重要。

瑞利散射 (Rayleigh Scattering)

瑞利散射，也称相干散射，是光子与整个原子发生的弹性碰撞。光子被原子整体吸收后，立即发射出一个能量和方向都与入射光子完全相同的次级光子。

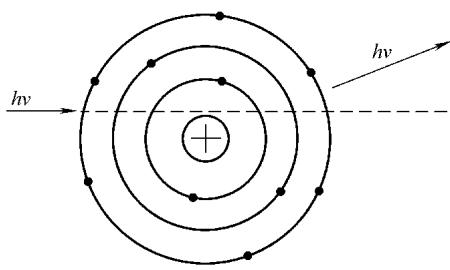
图11 瑞利散射示意图

这个过程没有能量损失，仅仅改变了光子的传播路径。瑞利散射的概率在低能量、高原子序数物质中较为显著，但通常对总衰减的贡献远小于光电效应和康普顿效应。

理解这几种效应的竞争关系至关重要：在不同能量和材料条件下，某一种效应会占据主导，这直接决定了检测图像的衬度来源和伪影特征。如果您在实际工作中也面临类似的图像解读或定量分析挑战，我们非常乐意与您一同探讨解决方案。

4. 射线的衰减规律：成像的基础

射线穿过物体时，由于上述各种相互作用（吸收和散射），其强度会随穿透厚度的增加而减弱，这就是衰减。正是这种可预测的衰减规律，使我们能够通过测量透射射线的强度来反推物体的内部信息。

单色窄束射线的指数衰减

对于一束能量单一（单色）、准直良好（窄束）的射线，其强度衰减遵循经典的指数定律，也称比尔-朗伯定律：

I = I₀e⁻μX

式中：

• I₀ 是入射射线强度
• I 是穿过厚度为X的物体后的透射射线强度
• X 是吸收体的厚度
• μ 是线衰减系数，表示单位厚度物质对射线的衰减能力，单位通常为 cm⁻¹。

线衰减系数 μ 是材料和射线能量的函数，它等于所有相互作用（光电效应τ、康普顿散射σ_C、瑞利散射σ_R、电子对效应κ）的线性衰减系数之和：

μ = τ + σ_C + σ_R + κ

为了消除材料密度的影响，理论研究中更常用质量衰减系数 μ_m：

μ_m = μ/ρ

其中 ρ 是物质的密度。质量衰减系数仅与元素组成和射线能量有关。

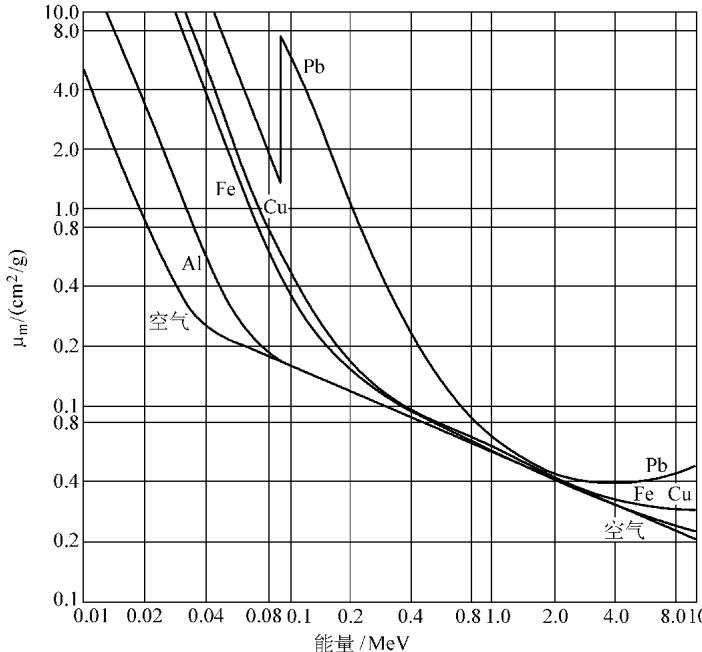
图12 几种金属的质量吸收系数与光子能量的关系

在实际应用中，还有一个非常直观的参数——半值层（HVL, T_1/2），它指能使入射射线强度衰减一半的材料厚度。它与线衰减系数的关系为：

T_1/2 = 0.693 / μ

半值层越小，说明材料对该能量射线的屏蔽能力越强。

表3 部分元素的质量衰减系数 μ_m (单位: cm²/g)

宽束连续谱射线的复杂情况

在实际工业检测中，我们面对的往往是能量不单一（连续谱）且非理想准直的宽束射线。

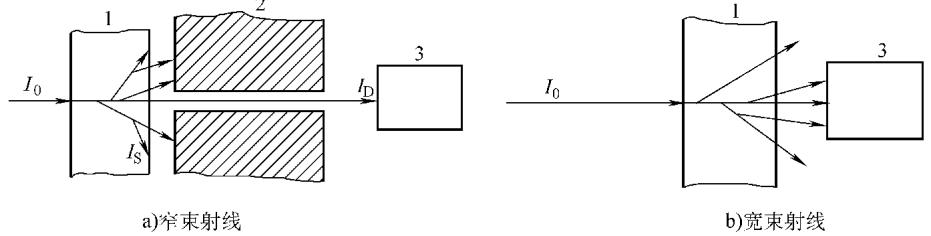
图13 宽束与窄束射线示意图（1—工件 2—准直器 3—探测器）

这种情况下，到达探测器的射线不仅包括沿直线传播的一次射线（I_D），还包含了大量在工件内部经过康普顿效应等散射后到达探测器的散射线（I_S）。因此，总的透射强度 I = I_D + I_S。

为了描述这种复杂情况，引入了积累因子 B (Buildup Factor)：

B = (I_D + I_S) / I_D = 1 + n

其中 n = I_S / I_D，称为散射比。积累因子B恒大于1，它量化了散射线对总信号的贡献。于是，宽束射线的衰减规律修正为：

I = B * I₀e⁻μX

散射线的存在会使图像模糊，降低缺陷的可探测性。因此，要获得一张信噪比高、结果可靠的射线检测图像，对设备参数配置、准直器使用、滤波片选择以及散射线校正算法都有极高要求。这正是专业检测实验室的核心价值所在。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测材料射线探伤，可靠准确。欢迎沟通交流，电话19939716636