系统可靠性基础：串联、并联与混合系统模型解析

在工程实践中，一个完整的系统通常由多个独立的元器件组合而成。系统的整体可靠性（R_S）并非孤立存在，而是直接取决于其构成单元——即单个元器件的可靠性（R_i）。理解这种依赖关系，是进行可靠性设计与分析的基石。

串联系统：木桶效应的数学诠释

在许多应用场景中，系统的正常运行以其所有组件的正常运行为前提。任何一个组件的失效，都会导致整个设备的瘫痪。这种“一损俱损”的逻辑关系，就是典型的串联系统。例如，一辆汽车的可靠性，既依赖于发动机，也依赖于轮胎。尽管发动机和轮胎不直接相互作用，但在功能上它们构成了串联关系。

这种功能结构可以抽象为图2a所示的串联系统模型。

对于一个串联系统，其在特定时间 t 的系统可靠性，是所有元器件可靠性的乘积。这源于基础的概率论法则：

R<sub>S,serial</sub>(t) = R₁R₂...Rₙ = Π Rᵢ(t)

或者，我们也可以用失效概率 F 来表达（F = 1 - R）：

F<sub>S,serial</sub>(t) = 1 - Π [1 - Fᵢ(t)]

从这两个简单的关系式中，我们可以推导出几个至关重要的结论：

• 组件越多，系统可靠性越低：在元器件可靠性给定的情况下，增加串联组件的数量会指数级地拉低整个系统的可靠性。
• 必须提升组件可靠性：要保证系统的高可靠性，唯一的途径就是提升每一个元器件自身的可靠性。

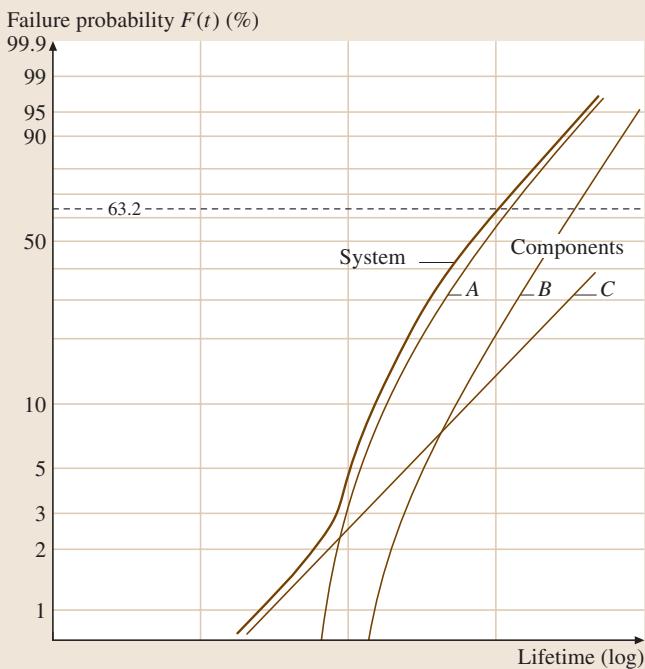图1. 串联系统可靠性与元器件可靠性的关系（以n=3为例）。系统可靠性曲线（粗线）始终低于最不可靠的那个元器件。在此图中，系统可靠性主要由元器件A或C决定，而可靠性较高的B对整体影响则小得多。

一个无法回避的事实是：串联系统的可靠性，绝不会优于其最薄弱的环节。

我们来看一个直观的例子。假设一个由10个元器件构成的系统，目标可靠性为0.9。为简化计算，我们假定所有元器件的可靠性 Rᵢ 相同。那么，每个元器件的可靠性必须达到：

Rᵢ = 0.9¹ᐟ¹⁰ ≈ 0.989

这是一个相当高的要求。如果其中9个组件的可靠性是0.989，而第10个组件的可靠性仅为0.8，那么整个系统的可靠性将急剧下降至：

Rₛ = 0.989⁹ × 0.8 ≈ 0.72

若我们将系统中的组件数量从10个增加到20个，为了维持0.9的系统可靠性，对单个组件可靠性的要求会从0.989进一步提升到0.995 (Rᵢ = 0.9¹ᐟ²⁰ ≈ 0.995)。

这个例子清晰地揭示了系统可靠性对元器件可靠性的高度敏感性，也说明了在工程设计中我们为何要对元器件施加如此严苛的可靠性要求。

在威布尔分布图（Weibull plot）中，这种关系可以被更直观地可视化。如图1所示，对于一个三组件系统，代表系统整体的威布尔分布曲线（粗线）总是位于所有元器件曲线的左侧，这意味着系统的寿命预期总是更短。这也引出了另一个有趣的工程问题：由于系统可靠性对元器件可靠性评估的敏感性，在进行威布尔分析时，是选择双参数还是三参数模型就显得尤为重要。如果一个场景本应使用三参数分布，却误用了双参数模型，往往会导致对失效概率的过高估计，进而造成设备设计的过度冗余（over-dimensioning）。尤其在机械工程领域，设备的强度与材料用量直接相关，这种过度设计会从经济和环境角度带来不必要的浪费。

并联系统与冗余设计

当系统中包含功能重复的元器件时，我们就引入了“冗余”（Redundancy）的概念。这些能够相互替代的组件，在系统结构中表现为并联关系，如图2b所示。

与串联系统截然相反，增加冗余的并联组件能够有效提升系统可靠性。这一点在并联系统的计算公式中得到了体现。在并联模型中，我们相乘的是各个组件的失效概率 F(t)，而非可靠性 R(t)：

F<sub>S,parallel</sub>(t) = F₁F₂...Fₙ = Π Fᵢ(t)

这个公式的逻辑在于，只有当所有并联的组件都失效时，系统才会整体失效。将其转换为可靠性函数 R(t) = 1 - F(t)，则得到：

R<sub>S,parallel</sub>(t) = 1 - [(1 - R₁)(1 - R₂)...(1 - Rₙ)] = 1 - Π [1 - Rᵢ(t)]

混合系统

在现实世界中，绝大多数系统都是串联与并联结构的结合体，即混合系统（如图2c）。对于这类系统，其可靠性可以通过布尔代数（Boolean algebra）的法则进行计算。原理上，就是将系统分解为若干个串联和并联的子系统，分别计算后再组合。

例如，对于图2c所示的功能结构，其系统可靠性 Rₛ 的计算方式如下：

Rₛ = R₁ × R₂ × [1 - (1 - R₃)(1 - R₄)] × R₅

其中 [1 - (1 - R₃)(1 - R₄)] 部分即为一个并联子系统的可靠性。

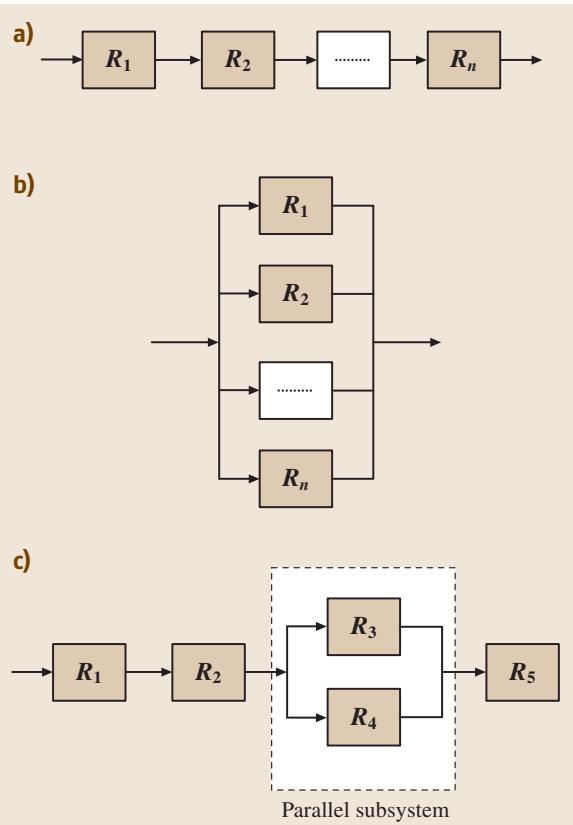图2. (a) 串联系统；(b) 并联系统；© 混合系统

可靠性工程的现实困境与未来趋势

尽管上述模型为系统可靠性分析提供了理论框架，但在日常的工程实践中，我们仍面临诸多挑战。

1. 元器件失效数据的匮乏：这是实践中最核心的难题。要运用上述模型进行计算，我们需要的不仅仅是一个简单的“设备寿命”值，而是能够描述其失效行为的完整威布尔参数，包括平均寿命和离散程度。然而，这类数据并未在公开数据库中得到充分记录和共享，少数例外是电子设备的失效率和金属部件的结构耐久性数据。获取精确、可靠的元器件失效数据，是进行有效系统可靠性预测的前提。这正是专业检测实验室的核心价值所在，通过系统性的实验设计和数据分析，为可靠性工程提供关键输入。 精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测材料可靠性测试，可靠准确。欢迎沟通交流，电话19939716636

2. 系统复杂性的与日俱增：当今的系统设计呈现出两大趋势：(a) 系统本身正变得越来越复杂；(b) 机械与电气组件被深度集成，共同实现系统功能，例如各类线控技术（X-by-wire）。这类机电一体化（Mechatronic）系统，正成为可靠性工程领域未来的主要挑战之一。

3. 新材料带来的未知数：挑战还来自于新材料的应用。许多机电一体化系统开始采用新型智能材料（Smart Materials）作为执行器或传感器，例如铁电/压电陶瓷、形状记忆合金等。尽管过去几十年学界对这些材料进行了大量研究，但它们在长期服役下的失效机理仍未被完全理解。特别是在复杂的服役条件（如电、机、热多场耦合应力）下，究竟会发生何种失效，以及其失效概率函数如何表征，这些问题至今仍是悬而未决的研究课题。