在半导体材料的研发与生产过程中,对其电学特性的精准表征是决定器件性能与成品率的基石。无论是体材料、半导体晶圆还是外延层、层叠结构,电导率 (Conductivity) 都是一个无法绕开的核心参数。
电导率 σ (单位: S/cm) 与材料的另一个基本属性——电阻率 ρ (单位: Ω·cm) 互为倒数关系:
$$ /sigma = /frac{1}{/rho} $$
从微观层面看,电导率由材料内部的载流子性质决定。对于以电子导电为主的半导体,其电导率可以由以下基本性质计算得出:
$$ /sigma = q/mu n $$
其中,q 为元电荷 (1.602 × 10-19 As),μ 为载流子迁移率 (单位: cm2/Vs),n 为载流子浓度 (单位: cm-3)。
当电子和空穴两种载流子对导电都有贡献时,总电导率则为两者之和:
$$ /sigma = q/mu_{/mathrm{n}}n + q/mu_{/mathrm{p}}p $$
其中,n 和 p 分别代表电子和空穴浓度,μn 和 μp 分别是它们的迁移率。下表概述了半导体的一些关键电学性质及其对应的表征方法。
表1:部分半导体属性及其相关表征方法一览
| 属性 | 符号 | 表征方法 |
|---|---|---|
| 电阻率 | ρ | 四探针法, 范德堡法 |
| 电导类型 | (n-型或p-型) | 热探针法, 霍尔效应 |
| 载流子浓度 | n, p | 霍尔效应, 电容-电压 (C-V) 测试 |
| 载流子迁移率 | μn, μp | 霍尔效应与电阻率联测 |
| 补偿比 | NA/ND, ND/NA | 霍尔系数的温度依赖性分析 |
| 深度掺杂分布 | N(x) | 电容-电压 (C-V) 测试, 结合选择性剥层的霍尔效应, 斜面样品上的扩展电阻法 |
| 扩散长度 | Ln, Lp | 结光电流法, 电子束感应电流 (EBIC) |
| 饱和漂移速度 | νn,sat, νp,sat | I-V 分析 (开尔文法) |
| 电子或空穴的电离率 (碰撞电离) | αn, αh | 温控 I-V 分析 |
| 少子寿命 | τn, τp | I-V 分析, 光电导法 |
| 深能级态 (陷阱): 密度, 热发射率, 俘获截面, 能级位置 | Nt, en, ep, σn, σp, Et | 深能级瞬态谱 (DLTS) |
在众多表征方法中,四探针法是测量体材料和薄层电阻率的经典标准方法。该方法在硅 (Si) 和锗 (Ge) 的测量中已非常成熟,同时也广泛适用于砷化镓 (GaAs)、磷化铟 (InP) 等 III-V 族化合物半导体。若将此方法应用于斜面样品,还可以推导出沿深度方向的电阻率分布(即扩展电阻法)。
四探针法的基本测量装置(可参考 DIN Norm 50431 等标准)如图1所示。测量头由四根等间距 (例如 s = 1 mm) 的弹簧加载探针组成,以一定的压力压在半导体样品表面。这个压力需要足够大以确保形成良好的近欧姆接触,但又必须足够轻柔,以免对样品造成可见的损伤。
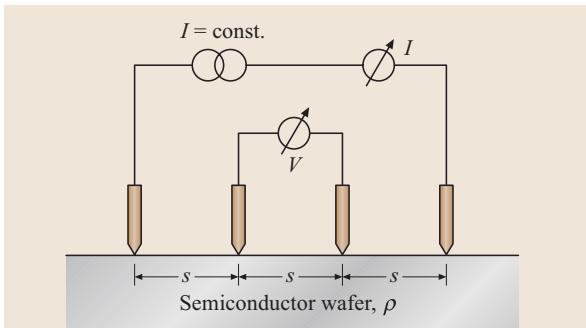
图1:在半无限大半导体晶圆上进行四探针测量的示意图,材料电阻率为 ρ
测量时,电流 I 通过外侧的两根探针注入样品,而内侧的两根探针则用于测量电压 V。这种结构类似于开尔文 (Kelvin) 连接,其精妙之处在于:假设我们使用一个具有近乎无限大源阻抗的恒流源和一个具有近乎无限大输入电阻的电压表,那么由电流流过探针接触点所产生的任何接触电压降都可以被忽略。
样品的电阻率 ρ 可以通过以下通用公式计算:
$$ /rho = /frac{V}{I} c $$
这里的 c 是一个与几何形状相关的修正因子,其值取决于样品的尺寸和探针间距。为了确保测量误差低于1%,所有样品配置都必须满足以下几个关键约束条件:
a) 探针与半导体之间形成近欧姆接触。
b) 测量电流 I (通常在mA量级) 引起的样品温升可忽略不计。
c) 无过剩载流子注入,避免产生额外的电导(即在暗环境下测量)。
d) 无由极端表面电势引起的表面能带弯曲,否则会导致表面积累层或反型层,从而干扰对体电导的真实测量。
这些条件的控制,尤其是在处理非标准样品或复杂层状结构时,对设备精度和操作经验提出了很高的要求。这正是专业检测实验室的核心价值所在。
精工博研测试技术(河南)有限公司(原郑州三磨所国家磨料磨具质量检验检测中心),央企,国字头检测机构,专业的权威第三方检测机构,专业检测半导体材料电性,可靠准确。欢迎沟通交流,电话19939716636
接下来,我们将针对几种典型的样品几何形状,给出修正因子 c 的具体形式。
当测量对象是在半绝缘衬底上生长的、横向尺寸可视为无限大的薄层时(如图2),其电阻率 ρ (Ω·cm) 可通过以下公式从测得的电压 V 和电流 I 推导出来:
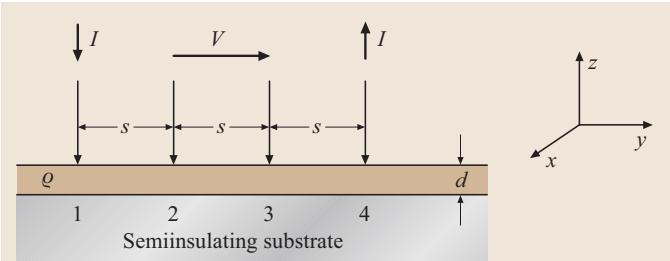
图2:在厚度为 d、电阻率为 ρ 的无限大薄层上应用四探针法;被测层由半绝缘衬底隔离
$$ /rho = /frac{V}{I} d/frac{/pi}{/ln 2} $$
在这个场景下,几何修正因子 c 等于 d * π / ln(2)。值得注意的是,该公式的精度与层厚 d 和探针间距 s 的相对大小有关。如果层厚 d 达到探针间距 s 的一半,计算出的电阻率误差将接近1%;如果 d 等于 s,误差会激增至8%。在实际应用中,通常使用 1 mm 的探针间距,因此对于厚度在 1-10 μm 范围内的薄层,这种系统误差完全可以忽略。该解法也适用于所有样品横向尺寸远大于三倍探针间距的情况。
对于半无限大的体样品(如图3),其电阻率 ρ (Ω·cm) 的计算公式变为:
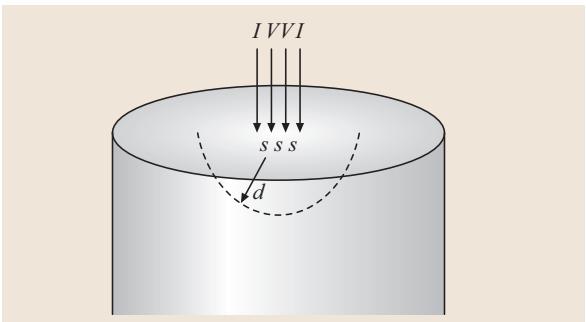
图3:在电阻率为 ρ 的半无限大体样品上应用四探针法;测量体积的半径约由 d > 3.5s 定义
$$ /rho = /frac{V}{I} s2/pi $$
此公式成立的前提是,样品的厚度 d 必须大于3.5倍的探针间距 s,以确保电流场分布符合半无限空间的模型。
在实际科研和生产中,样品往往既不是无限大薄层,也不是半无限大块体。对于尺寸有限的矩形样品(a × b × d),如图4所示,需要更复杂的修正方案。
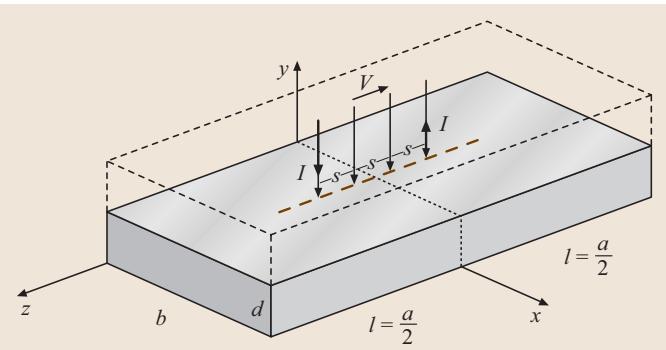
图4:在尺寸为 a×b×d、电阻率为 ρ 的矩形薄层上应用四探针法;被测层可由下方的半绝缘衬底或pn结隔离
解决这类问题可以采用有限元等数值方法。这里介绍一种由 Hansen 提出的解析方法,它易于在桌面计算机上实现。该方法通过分离变量法求解拉普拉斯方程,并通过镜像法(如图中虚线所示)施加标准边界条件,而不改变原始样品内的电场和电流线分布。通过级数展开,可以从测量的 I-V 值、样品几何数据 (a, b, d) 以及探针间距 s 推导出电阻率 ρ:
$$ /rho = /frac{V}{I}/left(/frac{s}{bd} +/frac{8}{bd}/sum_{m = 0}^{/infty}/sum_{n = 0}^{/infty} /frac{/cosh/beta/left(l - /frac{3s}{2}/right)/sinh/left(/beta/frac{s}{2}/right)}{/left(1 + /delta_{0,m}/right)/left(1 + /delta_{0,n}/right)/beta/cosh/left(/beta l/right)}/right)^{-1} $$
其中 (m, n) 不等于 (0, 0),并且:
$$ /beta = /frac{2/pi}{b}/left[m^2 +/left(/frac{nb}{2d}/right)^2/right]^{1 / 2} $$
δr,s 是克罗内克符号 (当 m=0 时 δ0,m=1,当 m>0 时为0)。
当样品包含两个相邻的同类型导电层(层1和层2),它们各自具有不同的薄层载流子浓度 n1,2 (cm-2) 和迁移率 μ1,2 (cm2/Vs),共同对总的薄层电导 δs 有贡献时,其等效的薄层载流子浓度 ns 和等效迁移率 μs 可以通过以下混合电导模型计算:
$$ n_{/mathrm{s}} = /frac{(/mu_{1}n_{1} + /mu_{2}n_{2})^{2}}{(/mu_{1}^{2}n_{1} + /mu_{2}^{2}n_{2})} $$
$$ /mu_{/mathrm{s}} = /frac{(/mu_{1}^{2}n_{1} + /mu_{2}^{2}n_{2})}{(/mu_{1}n_{1} + /mu_{2}n_{2})} $$
此模型假设相邻的同型层要么生长在半绝缘缓冲层上,要么通过一个pn结与衬底隔离。因此,在该双层混合电导模型中,衬底或缓冲层的电导应被视为可忽略不计。
最后,一个通用的操作提示:对于硅和锗等硬质材料,四探针的针压可达 50p 左右;而对于像 InP 这样更为敏感的 III-V 族材料,针压则需降低至 5p 左右,以防损伤样品。如果您在实际工作中也面临类似的薄膜或异形样品电阻率测试挑战,我们非常乐意与您一同探讨解决方案。


 首页
首页
 检测领域
检测领域
 服务项目
服务项目
 咨询报价
咨询报价