聚合物薄膜气体输运特性的动力学测量

通过对气体穿过均匀薄膜过程的动力学进行建模与测量，我们有机会在单次实验中，一举获得材料的溶解度（S）、扩散系数（D）和渗透系数（P）这三个核心输运参数。整个过程的物理基础，由菲克第二定律（Fick’s second law）所描述，它揭示了渗透物浓度（C）随时间和位置的变化关系。

$$ /frac{/partial C}{/partial t} = /frac{/partial}{/partial x}/left(D_{/mathrm{eff}}/frac{/partial C}{/partial x}/right) $$

该偏微分方程的解析解，强依赖于实验的初始条件、边界条件，以及一个关键变量——扩散系数（D）是否随浓度变化。当扩散系数是浓度的函数时，求解过程会变得相当复杂。然而，Crank和Park的研究表明，即便扩散系数实际上随浓度变化，基于恒定有效扩散系数（D_eff）假设得到的解，在许多情况下依然适用。这种近似处理足以精确地拟合大多数实验数据，但必须明确，由此得到的扩散系数应被理解为一个在整个浓度范围内的平均有效值。

恒定扩散系数的理想模型

在最简化的情景中，我们假设在整个目标浓度区间内，气体的扩散系数是一个常数。这个假设对于在橡胶态聚合物中低吸附性的渗透物通常是成立的。但这里需要一丝审慎，因为即便气体吸附行为仍然遵循亨利定律（即溶解度与压力无关），扩散系数也可能已经表现出对浓度的依赖性。

在一个典型的实验设定中，薄膜在初始时刻（t=0）具有均匀的初始浓度C₀。当t>0时，通过改变接触气体的压力，将薄膜的一个表面（x=0）暴露于恒定浓度C₂的环境中，而另一表面（x=l）则暴露于浓度C₁的环境中。在此边界条件下，菲克第二定律的解析解形式相当复杂：

$$ /begin{array}{l}{C = C_2 + (C_1 - C_2)/frac{x}{l}}// {+/frac{2}{/pi}/sum_{n = 1}^{/infty}/frac{C_1/cos n/pi - C_2}{n}}// {/times /sin /left(/frac{n/pi x}{l}/right)/exp /left(-Dn^2/pi^2 t / l^2/right)}// {+/frac{4C_0}{/pi}/sum_{m = 0}^{/infty}/frac{1}{2m + 1}/sin /left(/frac{(2m + 1)/pi x}{l}/right)}// {/times /exp /left[-D(2m + 1)^2/pi^2 t / l^2/right].} /end{array} $$

直接测量薄膜内部渗透物浓度随时间和位置的分布是极为困难的，因此在实践中很少采用。取而代之的是测量一个更易于操作的物理量：穿出薄膜的气体通量。通常有两种主流方法来监测这一动力学过程：瞬态渗透法和重量法（吸附或脱附）。

瞬态渗透法：时间滞后技术的应用

在瞬态渗透研究中，初始浓度C₀和下游浓度C₁均设定为零。在实验开始后，从薄膜下游侧（x=l）扩散出来的气体分子被收集在一个已知大小的封闭体积中。通过监测该封闭体积内气体累积的速率，可以方便地计算出气体通量[-D(∂C/∂x)_x=l]。在任意时刻t，穿过膜的总气体量Q_t由下式给出：

$$ /begin{array}{l}{Q_t = /int_0^t -D/Big(/frac{/partial C}{/partial x}/Big){x = l}/mathrm{d}t}// {= /frac{DtC_2}{l} -/frac{lC_2}{6} -/frac{2lC_2}{/pi^2}}// {/times /sum{n = 1}^{/infty}/frac{(-1)^n}{n^2}/exp /bigl (-Dn^2/pi^2 t / l^2/bigr),} /end{array} $$

当时间趋于无穷大（t → ∞），气体通量达到稳态时，上式可以简化为一个线性方程：

$$ Q_{t} = /frac{DC_{2}}{l}/left(t - /frac{l^{2}}{6D}/right) $$

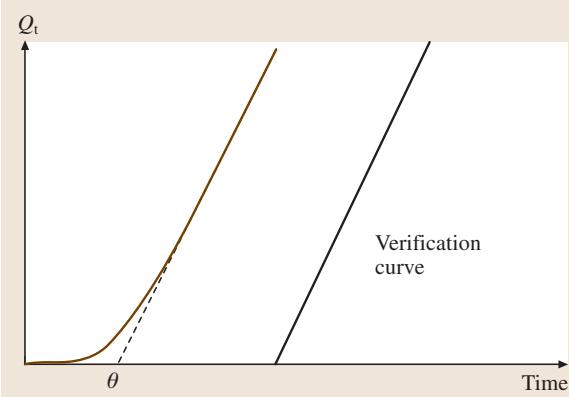图1. 瞬态渗透实验中累积渗透量Q_t随时间变化的典型曲线

典型的累积渗透量与时间的关系曲线如图1所示。当渗透过程进入稳态后，Q_t与时间t呈现线性关系。将这条直线外推至时间轴，其截距被定义为“时间滞后（time lag）”，用符号θ表示，其值为l²/6D。由此，扩散系数D可以通过一个非常简洁的公式计算得出：

$$ D = l^2 /6/theta $$

这套精妙的理论分析最早由Daynes在1920年提出。到了1939年，Barrer及其同事成功研制出一套能够精确测量聚合物中时间滞后和稳态流的系统。利用这种方法，渗透系数、扩散系数和溶解度系数得以在一次实验中被同时确定。

重量法：监测吸附与脱附动力学

另一种有效的方法是监测聚合物薄膜的重量变化，从而追踪气体进出薄膜的动态过程。在一个典型的重量法实验中，一块具有初始气体浓度C₀的聚合物薄膜被突然置于一个恒定气体压力p₂的环境中。这意味着在t>0时，薄膜的两个表面（x=0和x=l）的浓度瞬间达到与p₂相平衡的浓度C₂。

• 当C₂ > C₀时，发生吸附，渗透物分子向薄膜内部扩散。
• 当C₂ < C₀时，发生脱附，渗透物分子从薄膜中逸出。

这些过程的动力学由以下方程描述：

$$ /frac{M_{/mathrm{t}}}{M_{/infty}} = 1 - /frac{8}{/pi^2}/sum_{n = 0}^{/infty}/frac{1}{(2n + 1)^2}/exp /bigl [-D(2n + 1)^2/pi^2 t / l^2/bigr ] $$

其中，M_t和M_∞分别代表在时间t和达到平衡时，薄膜中吸附或脱附的渗透物总量。对于一个横截面积为A、厚度为l的薄膜，M_t和M_∞的定义如下：

$$ M_{/sf t} = /left|A/int_{0}^{l}C(x,t)/mathrm{d}x - C_{0}Al/right| $$

$$ M_{/infty} = |C_2 - C_0|Al $$

因此，通过测量样品重量随时间的变化，并将实验数据与上述动力学方程进行拟合，便可求得扩散系数。为了简化分析，可以采用两种近似方法：

1. 长时近似：当M_t/M_∞ > 0.7时，级数中的高阶项(n>0)可以忽略不计，方程简化为： $$ /ln /bigl (1 - M_{/sf t} / M_{/infty}/bigr) = /ln /frac{8}{/pi^2} -/frac{D/pi^2}{l^2} t $$ 此时，通过绘制ln(1 - M_t/M_∞)对时间t的曲线，可以从斜率中直接求出扩散系数D。

2. 短时近似：在吸附/脱附的初始阶段（M_t/M_∞ < 0.6），存在另一个解析解的简化形式： $$ /frac{M_{/sf t}}{M_{/infty}} = /left(/frac{16D}{/pi l^2}/right)^{1 / 2}t^{1 / 2} $$ 该式预测，分数吸收（或脱附）量与时间t的平方根成线性关系。因此，绘制M_t/M_∞对t^1/2的曲线，同样可以从斜率中计算出扩散系数D。

此外，通过平衡时的吸附/脱附量M_∞和初始浓度C₀，可以计算出材料的溶解度系数S_A：

$$ S_{/mathrm{A}} = /frac{1}{p_{2}}/Big(C_{0}/pm /frac{M_{/infty}}{Al}/Big) $$

式中，p₂是平衡时的气相压力，吸附过程取“+”号，脱附过程取“-”号。

无论是时间滞后法还是重量法，都需要精密的实验控制和准确的数据分析来保证结果的可靠性。特别是在处理复杂的非理想情况时，对理论模型的深刻理解和对实验数据的专业解读至关重要。 精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测高分子薄膜气体渗透性，可靠准确。欢迎沟通交流，电话19939716636

扩散系数可变时的复杂情况

在许多实际体系中，渗透物的扩散系数会随着其自身浓度的变化而变化。例如，对于在橡胶态或玻璃态聚合物中具有强吸附性的渗透物，当其浓度（或活性）足够高时，会引起聚合物的溶胀，进而改变聚合物的物理性质（如玻璃化转变温度、自由体积分数等），最终导致扩散系数的改变。

Frisch和Crank等学者已经对这种浓度依赖性扩散进行了深入的理论研究，并发展了相应的解析和数值方法。然而，严格来说，这些处理方法大多要求预先知道扩散系数与浓度之间的函数关系。相比之下，稳态测量方法（如前述章节所讨论）提供了一条无需预设扩散系数-浓度函数关系，便能可靠评估扩散、溶解和渗透系数的途径。

总而言之，测量聚合物薄膜气体输运性质的实验方法多种多样。但其核心原理大都归结为直接测量穿过薄膜的气体通量，或是测量薄膜对气体的吸收量（即溶解度）。扩散系数通常是基于前述理论，从渗透性和溶解度的测量结果中间接推导出来的。后续章节将介绍测量这些气体输运性质的通用策略。