聚合物膜气体输运特性：稳态渗透过程详解

日期：2025-07-23 浏览：3

聚合物膜气体输运特性：稳态渗透过程详解

在致密或无孔聚合物薄膜中，气体分子的输运过程通常遵循经典的溶解-扩散机制（Solution-Diffusion Mechanism）。这一过程可以分解为三个连续的步骤，如下图所示：首先，在高压侧（上游），气体分子溶解进入薄膜的表面；接着，在浓度梯度的驱动下，溶解的气体分子在聚合物基体中进行扩散；最后，这些分子在低压侧（下游）的表面脱附出来。当气体与聚合物之间不发生化学反应时，溶解的渗透质（Penetrant）在膜内的扩散步骤，便成为整个输运过程的速率控制步骤。

我们可以用菲克定律（Fick’s Law）来描述气体组分A沿x方向穿过薄膜的一维通量（NA）：

$$ N_{/mathrm{A}} = -D/frac{/mathrm{d}C_{/mathrm{A}}}{/mathrm{d}x} +w_{/mathrm{A}}(N_{/mathrm{A}} + N_{/mathrm{P}}) /tag{1} $$

在此式中，D 代表气体在薄膜中的扩散系数，CA 是溶解气体的局部浓度，而 wA 则是气体A在薄膜中的质量分数。Np 是膜本身的通量，通常视为零。因此，该方程可以简化为：

$$ N_{/mathrm{A}} = -/frac{D}{1 - w_{/mathrm{A}}}/frac{/mathrm{d}C_{/mathrm{A}}}{/mathrm{d}x} /tag{2} $$

稳态渗透 (Steady-State Permeation)

对于厚度为 l 的薄膜，气体A的稳态渗透系数 PA 定义为：

$$ P_{/mathrm{A}}/equiv /frac{N_{/mathrm{A}}l}{p_2 - p_1} /tag{3} $$

其中，p2 和 p1 分别是上游（高压）和下游（低压）的压力。渗透系数的常用单位是巴勒（Barrer），1 Barrer = 1 × 10^-10 cm³(STP)·cm / (cm²·s·cmHg)。

将公式(2)和(3)结合，并从 x = 0（此时浓度为 C2）到 x = l（此时浓度为 C1）进行积分，可以得到：

$$ P_{/mathrm{A}} = D_{/mathrm{A}}/frac{C_2 - C_1}{p_2 - p_1} /tag{4} $$

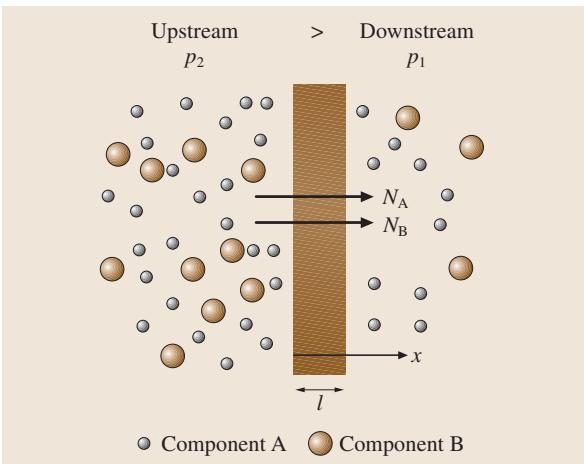
图1. 气体A和B穿过膜的输运过程示意图

这里的 DA 是在 C1 - C2 浓度范围内的浓度平均有效扩散系数：

$$ /begin{array}{l}{D_{/mathrm{A}} = /frac{1}{C_2 - C_1}/int_{C_1}^{C_2}/frac{D}{1 - w_{/mathrm{A}}}/mathrm{d}C}// {= /frac{1}{C_2 - C_1}/int_{C_1}^{C_2}D_{/mathrm{eff}}/mathrm{d}C,} /end{array} /tag{5} $$

式中，Deff 是局部有效扩散系数。

在实际操作中，直接测量气体的平均扩散系数颇具挑战。因此，研究人员通常会独立测量气体的渗透系数和溶解度，再通过计算间接推导出扩散系数。为了简化实验，通常将下游压力设置得远小于上游压力（p1 << p2），此时下游浓度也远小于上游浓度（C1 << C2）。在这种极限条件下，公式(4)简化为材料科学中一个极为重要的关系式：

$$ P_{/mathrm{A}} = D_{/mathrm{A}}/times S_{/mathrm{A}} /tag{6} $$

这里的 SA = C2 / p2，被称为表观吸附系数或渗透质A在聚合物中的溶解度。这个公式的精妙之处在于，它将复杂的渗透过程解耦为两个独立的物理量：动力学因素（扩散系数 DA）和热力学因素（溶解度系数 SA）。通过在上游压力 p2 下分别测量气体的渗透性和溶解度，我们就能计算出平均气体扩散系数 DA。需要明确的是，根据公式(5)，这个扩散系数是在 0 到 C2 浓度范围内的平均值。

要进一步获得在特定渗透质浓度 C2 下的局部有效扩散系数 Deff，则需要一个更为复杂的微分方程：

$$ D_{/mathrm{eff}}(C_2) = /left(P_{/mathrm{A}} + p/frac{/mathrm{d}P_{/mathrm{A}}}{/mathrm{d}p}/right){p_2}/left(/frac{/mathrm{d}p}{/mathrm{d}C_2}/right){p_2} /tag{7} $$

这个方程的求解，要求我们必须掌握渗透系数和溶解度随压力变化的详细数据。获取这些依赖关系是材料阻隔性能表征中的核心工作之一。

气体吸附等温线模型

聚合物中的气体吸附等温线，即气体在聚合物中的浓度 C 与气体压力 p 之间的关系，通常可以用一些经典模型来描述，如亨利定律（Henry’s law）、Flory-Huggins理论或双模吸附模型（dual-mode sorption model）。一旦测定了聚合物的气体吸附行为，就可以方便地计算出 dp/dC2 的值，代入公式(7)中。

1. 亨利定律 (Henry’s Law) 亨利定律描述了浓度 C 和压力 p 之间的线性关系：

$$ C = k_{/mathrm{D}}p /tag{8} $$

其中 kD 是溶解度系数，也称亨利定律常数。该定律通常适用于低浓度下（如 1 cm³(STP)/cm³ 聚合物）的轻质气体在橡胶态聚合物中的溶解。例如，在35°C下，N₂ 和 O₂ 在聚二甲基硅氧烷（PDMS）中的吸附行为在相当宽的压力范围内都遵循亨利定律。

2. Flory-Huggins 模型 对于在橡胶态聚合物中具有高溶解度的渗透质（如有机蒸汽），其浓度通常采用Flory-Huggins模型来描述：

$$ /ln a = /ln /phi_{2} + (1 - /phi_{2}) + /chi (1 - /phi_{2})^{2} /tag{9} $$

其中，a 是渗透质的活度（对于理想气体，a = p / p0，p0 是实验温度下渗透质的饱和蒸汽压），χ 是Flory-Huggins相互作用参数，φ2 是溶解在聚合物基体中渗透质的体积分数。体积分数 φ2 由下式给出：

$$ /phi_{2} = /frac{(C / 22414)V_{2}}{1 + (C / 22414)V_{2}} /tag{10} $$

这里的 V2 是渗透质在聚合物中的偏摩尔体积（cm³/mol），C 的单位是 cm³(STP)/cm³(聚合物)。当吸附气体浓度很低时（φ2 << 1），该模型可简化为亨利定律。而在高浓度下，该模型预测溶解度（即 C/p）会随压力升高而增大。例如，35°C下CO₂在聚环氧乙烷中的吸附行为就可以用此模型成功描述。

3. 双模吸附模型 (Dual-Mode Sorption Model) 该模型最初用于描述气体在玻璃态聚合物中的吸附。玻璃态聚合物同时包含平衡体积（对应亨利定律吸附位点）和非平衡的过剩体积（即微孔或朗缪尔吸附位点）。该模型表示为：

$$ C = C_{/mathrm{D}} + C_{/mathrm{H}} = k_{/mathrm{D}}p + /frac{C_{/mathrm{H}}'b p}{1 + b p} /tag{11} $$

在此模型中，C 由两部分构成：溶解在聚合物致密基区中的亨利模式浓度 CD，以及吸附在微孔中的朗缪尔模式浓度 CH。b 是朗缪尔亲和常数，表征渗透质与微孔之间的亲和力；CH' 是朗缪尔容量常数（单位：cm³(STP)/cm³ 聚合物），表征非平衡过剩体积的最大吸附容量。该模型也被扩展应用于描述杂化体系，如橡胶态聚合物与添加剂的共混物，其中添加剂可以是物理吸附气体的填料，或是与气体发生化学作用的溶解物种。

准确拟合这些模型，尤其是双模吸附模型，需要高质量、多压力点的渗透与吸附实验数据。这对于精确评估材料的阻隔性能和预测其在复杂工况下的行为至关重要。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测高分子材料气体阻隔性能，可靠准确。欢迎沟通交流，电话19939716636

渗透系数的压力依赖性

渗透系数对压力的依赖性通常采用经验方程来描述。例如，以下方程常用于描述橡胶态聚合物中气体渗透率的压力依赖性：

$$ P_{/mathrm{A}} = P_{/mathrm{A0}}(1 + m/Delta p) /tag{12} $$

其中 PA0 和 m 是常数，Δp = p2 - p1。

对于玻璃态聚合物，在 p1 = 0（即 Δp = p2）的条件下，常使用基于双模模型的以下方程：

$$ P_{/mathrm{A}} = k_{/mathrm{D}}D/bigg(1 + /frac{FK}{1 + bp_2}/bigg) /tag{13} $$

其中 K = CH'b / kD，而 D 和 F 是通过将模型与实验吸附和渗透数据拟合得到的常数。例如，研究人员可以通过将气体吸附等温线拟合到公式(11)来获得 kD、b 和 CH'，然后将不同上游压力下的渗透率数据拟合到公式(13)来获得 D 和 F。利用公式(12)或(13)，可以计算出 dPA/dp，再将其与从吸附模型中得到的 dp/dC2 一同代入公式(7)，即可计算出局部有效扩散系数 Deff。

膜的选择性

膜对气体A相对于气体B的理想选择性（αA/B）定义为它们的纯气体渗透系数之比：

$$ /alpha_{/mathrm{A / B}} = /frac{P_{/mathrm{A}}}{P_{/mathrm{B}}} = /left(/frac{D_{/mathrm{A}}}{D_{/mathrm{B}}}/right)/times /left(/frac{S_{/mathrm{A}}}{S_{/mathrm{B}}}/right) /tag{14} $$

这个表达式明确指出，膜的整体选择性是扩散选择性（DA/DB，反映了分子尺寸筛分能力）和溶解选择性（SA/SB，反映了聚合物对不同气体的亲和力差异）的乘积。

对于二元气体混合物，气体A对气体B的选择性（α*A/B）定义为：

$$ /alpha_{/mathrm{A / B}}^{*}/equiv /frac{y_{/mathrm{A}} / y_{/mathrm{B}}}{x_{/mathrm{A}} / x_{/mathrm{B}}} = /alpha_{/mathrm{A / B}}/frac{/Delta p_{/mathrm{A}} / x_{/mathrm{A}}}{/Delta p_{/mathrm{B}} / x_{/mathrm{B}}} /tag{15} $$

其中 yi 和 xi 分别是组分 i 在下游和上游气相中的摩尔分数，Δpi 是组分 i 穿过膜的压差。当低压侧压力远小于高压侧压力时，α*A/B 趋近于理想分离因子 αA/B。

上一篇:热导率、比热容与热扩散率：核心原理与测量技术选型指南

下一篇:聚合物中的导电现象及其物理基础

点击在线咨询

服务热线: