晶体材料的强化机制解析

晶体材料的流变应力，其本质由位错的运动所主导。基于这一核心原理，提升材料强度的路径可归结为两条截然不同的策略：一是近乎完美地消除所有位错，二是引入大量障碍物以阻碍位错的滑移。

第一条路径，即追求“无位错”的理想状态，在单晶须的制备中得到了验证。然而，这种方法极具局限性。随着晶须直径的增大，缺陷（包括位错）的引入变得不可避免，导致其强度急剧下降。因此，在工程实践中，我们更广泛地采用第二条路径——通过在微观结构中“设障”，有效钉扎位错。这催生了多种经典的强化技术，包括固溶强化、沉淀或弥散强化、加工硬化、细晶强化以及复相组织强化。以下将对这些阻碍位错运动的核心机制进行深入剖析。

固溶强化 (Solid-Solution Hardening)

当溶质原子（无论是间隙型还是替代型）进入基体晶格后，会因其尺寸效应或导致的弹性模量不均匀性，在局部产生晶格畸变。这种畸变场会与位错的应力场发生弹性相互作用，从而阻碍位错的运动。这种相互作用力是弹性的，位错在热激活的辅助下可以克服它。

其强化效果的增量（Δσ）可用以下经验公式来描述：

Δσ = Acⁿ

式中，A 是与材料相关的常数，c 代表溶质原子的浓度。指数 n 根据实验或理论推导，其值通常在 0.5 到 1.0 之间。简言之，溶质原子浓度越高，对位错的阻碍作用越强，材料的强度也越高。

加工硬化 (Workhardening)

如前所述，塑性变形过程会使材料内部的位错密度（ρ）急剧增加。新产生的可动位错在运动时，必须穿过由已有位错形成的复杂网络，即“位错林”。位错之间的相互作用分为两类：短程相互作用，如弹性交互、切割和反应等；以及由位错结构引发的内应力场导致的长程相互作用，典型的例子是位错在障碍物前塞积所产生的背应力。

无论是哪种模型，最终都导向一个相似的强化关系式，即 Bailey-Hirsch 关系：

Δσ = B√ρ

其中，B 为一个常数。该公式清晰地表明，材料的强度增量与位错密度的平方根成正比。

沉淀或弥散强化 (Precipitation or Dispersion Hardening)

在基体中弥散分布着细小的第二相粒子（沉淀相或弥散相）时，运动的位错线会与这些粒子发生相互作用。

当粒子较“软”时，位错线可以切过粒子继续前进，如图1(a)所示。其临界条件由下式给出：

Δσ = (aμb / λ)cos(φ/2)

这里，a 是常数，μ 是剪切模量，b 是位错的柏氏矢量大小，λ 是粒子的平均间距，而 φ 是位错线切过粒子所需的临界角。

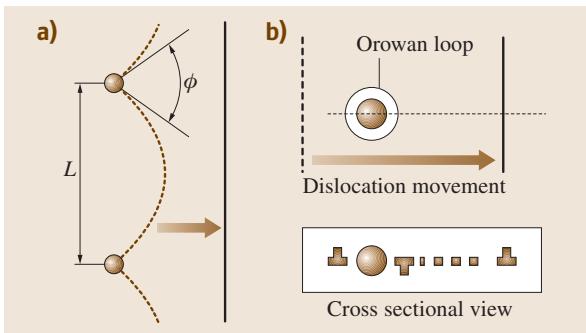
图1 (a) 切割机制与 (b) 奥罗万绕过机制示意图

当粒子非常“硬”，位错无法切过时（相当于临界角 φ = 0°），位错线会选择绕过粒子，并在粒子周围留下一个位错环，这个过程被称为奥罗万（Orowan）机制，如图1(b)所示。对于这种由强粒子主导的弥散强化，其强度增量可简化为：

Δσ = 2μb / λ

该式表明，第二相粒子的间距越小，对位错的阻碍作用越强，强化效果越显著。

细晶强化 (Grain-Refinement Hardening)

晶界是位错运动的天然强障碍。当位错运动至晶界时，其运动受阻并在此处塞积，从而在晶界附近产生显著的内应力，如图2所示。这种位错塞积所产生的背应力会阻碍后续位错的进一步运动，其原理与加工硬化中的长程相互作用类似。

塞积的位错数量与外加应力和滑移距离（即晶粒直径 d）有关，理论上可以推导出强化增量（Δσ）与晶粒尺寸的关系：

Δσ = kd⁻¹/²

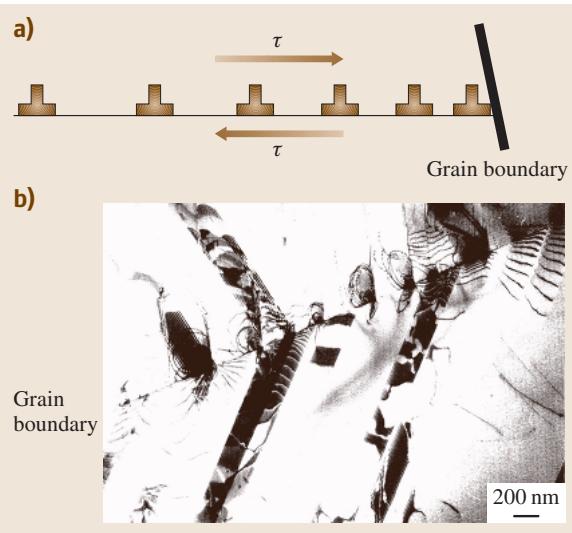
图2 (a) 晶界处的位错塞积模型与 (b) 高氮奥氏体钢的TEM显微照片

对于细晶强化的机理，还存在其他几种解释。例如，晶界附近由于局部内应力很高，会激活多个滑移系，导致该区域位错密度增加，其强化效果同样可以用 Bailey-Hirsch 关系（Δσ = B√ρ）来描述，最终也能推导出与上式形式相同的关系。另一种解释认为，为了缓解晶界处的高度局部应力，相邻晶粒的晶界可以作为位错源，发射出新的位错。

由于上述关系式最早由 Hall 和 Petch 基于大量实验数据提出，因此被称为霍尔-佩奇关系（Hall-Petch relation）。在实际材料中，细晶强化往往是多种效应叠加的结果，但霍尔-佩奇关系式能够相当准确地描述晶粒细化带来的强度提升。精确测定材料的晶粒度、位错密度和分布，对于验证和应用这些强化理论至关重要。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测材料微观结构与力学性能评价，可靠准确。欢迎沟通交流，电话19939716636

复相组织强化 (Duplex Structure Hardening)

当材料中第二相的尺寸与基体晶粒尺寸相当（即粗大的多相组织）时，奥罗万绕过等弥散强化模型便不再适用。在这种情况下，塑性变形会优先在较软的相中发生，导致应力在不同相之间重新分配，产生所谓的“相间应力”或平均内应力。

这种强化方式更接近于复合材料的强化原理。许多工程材料，如铁素体-珠光体钢、双相钢、α-β 黄铜等，都属于这一范畴。尽管已有微观力学模型来精确描述多相材料的变形行为，但在工程应用中，其流变应力通常可以用一个简单的混合法则来近似估算。对于一个两相合金：

σ = σ₁(1 - f) + σ₂f

式中，σ₁ 和 σ₂ 分别代表基体相和第二相的强度，f 是第二相的体积分数。

强化机制的叠加

在真实的工程材料中，上述强化机制往往不是独立作用，而是同时存在、相互叠加。因此，必须采用合适的叠加法则来估算材料的总强度。一个简化的叠加规则可以表示为：

σ = Σ(σᵢ)ᴺ

其中，σᵢ 代表第 i 种强化机制贡献的强度。当强障碍与弱障碍叠加时，指数 N 的值接近于 1；而当多种强障碍机制共同作用时，N 的值通常小于 1。