在当今的科研与工业设备中,电阻温度计(Resistance Thermometer)无疑是应用最广泛的温度传感器之一。其核心优势在于能够便捷地将温度信号转换为电子系统易于读取的电阻信号,从而轻松实现自动化温度控制闭环。在众多电阻温度计中,铂电阻温度计(Platinum Resistance Thermometer, PRT)尤为突出,它不仅是应用最广的类型,更是国际温标 ITS-90 中用于实现最高精度温度复现的内插仪器。当用于这一目的时,它被称为标准铂电阻温度计(Standard Platinum Resistance Thermometer, SPRT),其不同型号覆盖了从氢三相点(13.8033 K)到银凝固点(1234.93 K)的广阔温区。
金属材料的电阻源于导电电子在固体晶格原子或分子上的散射。其总电阻可以分解为两个部分:一部分是随温度变化的部分 R<sub>t</sub>,由晶格振动引起,随着内能增加而增大;另一部分是与温度无关的残余电阻 R<sub>0</sub>,由材料中的杂质和晶格缺陷造成。样品的总电阻便是这两部分之和:
$$ R(T) = R_t(T) + R_0 /tag{1} $$
这个在文献中被称为马西森定则(Mathiessen’s rule)的方程,可以进一步简化为一个更实用的形式:
$$ R(T) = R(0°C)(1 + αt) /tag{2} $$
其中,α 是电阻温度系数。从这个关系式可以看出,减少材料中的杂质或缺陷,会降低其在 0°C 时的电阻 R(0°C) 或残余电阻 R<sub>0</sub>,同时会增大电阻温度系数 α。这意味着,要制造性能优良的电阻温度计,就必须选用那些能够被高度提纯并能通过有效退火处理来消除内部缺陷的金属。
高纯度铂(Platinum)是目前最能满足马西森定则的材料,尽管卡伦德(Callendar)和后来的范杜森(van Dusen)发现其存在微小偏差。为了更精确地描述铂电阻与温度的非线性关系,公式(2)被修正为著名的卡伦德-范杜森方程(Callendar-van Dusen equation):
$$ R(T) = R(0°C)[1 + At + Bt^2 + C(t - 100)t^3] /tag{3} $$
此方程中的系数数量级大致为:A ≈ 4 × 10<sup>-3</sup> °C<sup>-1</sup>,B ≈ -6 × 10<sup>-7</sup> °C<sup>-2</sup>,以及 C ≈ 4 × 10<sup>-12</sup> °C<sup>-3</sup>。
然而,铂电阻温度计的这种理想性能表现,只有在不受其他外界因素干扰时才能成立。在实际应用中,必须极力避免应力、机械冲击、振动、压力、湿度和腐蚀等干扰效应。其中,部分效应(如应力)可能由非受控的温度变化自身引发,而其他效应则可以通过谨慎操作来规避。对于那些难以避免的环境因素,则必须通过密封和屏蔽的结构设计来将其影响降至最低。
为了满足不同场景的需求,铂电阻温度计发展出了多种形态,尤其是在作为ITS-90标准仪器时,主要有以下几种类型,如表1所示。
表1:标准铂电阻温度计(SPRT)的主要类型
| 温度计类型 | 适用温区 | 典型电阻值 |
|---|---|---|
| 铠装式温度计, 50–60 mm长 | 13.8–430 K | 25.5Ω |
| 长杆式温度计, 450 mm长 | 84–933 K | 25.5Ω |
| 高温长杆式温度计 | 0.01–962°C | 0.25Ω |
标准的SPRT通常将高纯度铂丝绕制成线圈,封装在玻璃或石英护套内,并置于铂金管中。这种结构设计的初衷是为了使铂丝处于一种无应力且免受污染的状态,但也使其对冲击、振动或其他任何机械应力变得极为敏感。因此,SPRT一方面是稳定性极高、不确定度低于 1 mK 的温度标准器,另一方面却完全不适用于环境恶劣的工业现场。
那么,如何在工业应用中获得更可靠的测温器件呢?答案是对铂丝的支撑结构进行强化。但这不可避免地会在温度变化时给铂丝带来更大的应力,从而将测量不确定度增加到 10 mK 左右。所有线绕式器件还面临一个共同的缺点:热接触不良。热量主要通过封装管内的惰性气体和引线传递,导致其时间常数长达数秒。
作为替代方案,厚膜铂电阻应运而生。这类传感器可以直接粘贴在待测样品表面,显著改善了热接触,缩短了响应时间。它们的标称电阻值通常为 100Ω,非常适合环境严苛的场合和温度控制回路。当然,这种结构也付出了代价:它们更容易受到应力和污染的影响,测量不确定度也相应增大到 100 mK 左右。
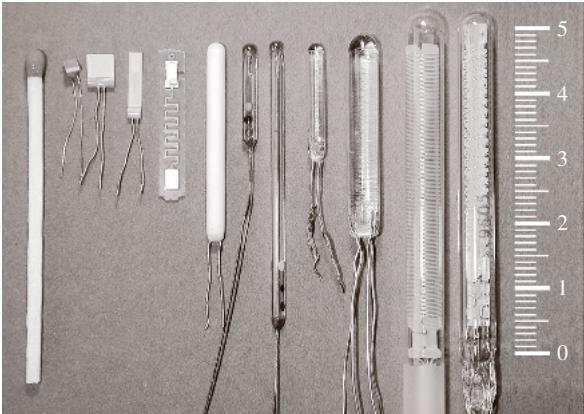
图1:(从左至右)三种厚膜 Pt-100 电阻;用于SMD贴片的 Pt-500 芯片电阻;陶瓷封装 Pt-100 电阻;两支玻璃封装 NTC 热敏电阻;玻璃封装 Pt-100 电阻;双支玻璃封装 Pt-100 电阻;长杆式 SPRT (Pt-25);铠装式 SPRT (Pt-25)
这些不同类型的电阻温度计大多已实现商业化生产,除非有极其特殊的需求,用户通常无需自行制作。
要将电阻信号转化为温度读数,需要精密的测量电路。目前主流的方案有两种:电位法(potentiometric method)和电桥法(resistance bridge),如图2所示。
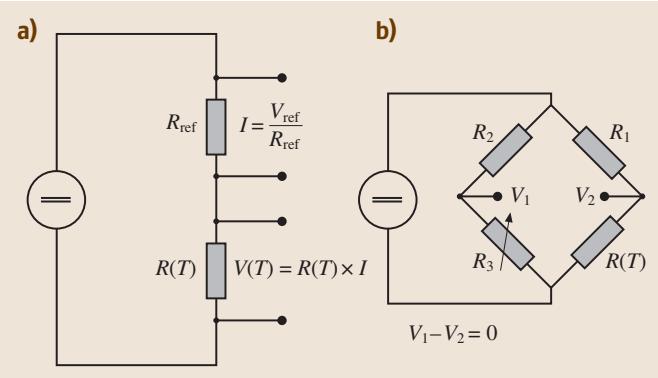
图2:电阻测量电路 (a) 电位法 (b) 电桥法
电位法是目前最常见的方案,尤其是在高精度电子元器件普及之后。其原理是将一个高精度的参考电阻 R<sub>ref</sub> 与待测的温度传感器串联。当一个恒定的电流 I 流过整个电路时,通过测量参考电阻两端的电压降,可以精确计算出电流值。接着,测量温度传感器两端的电压降 V(T),再次利用欧姆定律即可算出传感器的实时电阻 R(T)。
电桥法,特别是基于惠斯通电桥原理的电路,是另一种经典方法。电路由两个并联的支路构成,例如一个支路串联着电阻 R<sub>1</sub> 和传感器 R(T),另一支路串联着 R<sub>2</sub> 和 R<sub>3</sub>。在“平衡电桥”模式下,需要调节可变电阻 R<sub>3</sub>,直到两个支路中间点的电压差为零。这意味着在每个待测温度 T 下,都需要进行一次平衡调节。此时,传感器的电阻值由下式给出:
$$ R(T) = R_1(R_3 / R_2) /tag{4} $$
如果仅在某个特定温度(如 T<sub>0</sub>)下对电桥进行一次平衡,那么在其他温度下,电桥的输出电压 V<sub>1</sub> - V<sub>2</sub> 将不再为零。在 T<sub>0</sub> 附近的一个线性区间内,该输出电压与测量的温度成正比。
在实际测量中,连接传感器的导线本身也存在电阻,它会与传感器串联,引入误差。消除这一误差的最佳方法是采用四线制测量法。在这种配置下,两根独立的电压测量导线被连接到尽可能靠近传感器的位置。如果电压表的内阻足够大(接近无穷大),那么流过电压测量导线的电流就可以忽略不计,其自身的电压降也就可以忽略,从而精确测得传感器两端的真实电压。
如果成本或布线条件受限,可以采用两线制,但精度会降低。对于导线材料,应优先选择电阻温度系数低的材质,并确保在测量过程中导线所处环境温度保持恒定,以维持其电阻不变。
作为一种折中方案,三线制在成本和精度之间取得了平衡。它只在传感器的一端连接一根独立的电压导线,通过测量“传感器+一根电流导线”的总压降,再减去另一根电流导线的压降(单独测量或假设相等)来进行补偿。
实现高精度的温度测量,不仅仅是选用一个好的传感器,更是一个系统工程,需要对电路设计、布线、屏蔽和数据处理等各个环节进行细致的考量。这正是专业检测实验室的核心价值所在。
精工博研测试技术(河南)有限公司(原郑州三磨所国家磨料磨具质量检验检测中心),央企,国字头检测机构,专业的权威第三方检测机构,专业检测高精度温度测量,可靠准确。欢迎沟通交流,电话19939716636
除了铂电阻,还有其他材料可用于制造电阻温度计,以满足特殊应用场景的需求。
铑铁(Rhodium-Iron)温度计:这种含有0.5%铁的铑合金温度计,在 0.5 K 至 30 K 的极低温区比铂电阻更灵敏,同时其有效工作范围可延伸至室温。市面上有电阻值在 20-50Ω 的线绕式和厚膜式两种产品。
半导体热敏电阻(Thermistor):这类由半导体材料制成的电阻温度计,包括负温度系数(NTC)和正温度系数(PTC)两种。NTC热敏电阻的阻值与温度的关系遵循指数定律:
$$ R(T) = A /exp(B / T) /tag{5} $$
与铂电阻相比,NTC在 -100°C 到 +150°C 的温区内,灵敏度要高出100倍以上(可达 3-6%/°C),且体积更小、响应更快。然而,它们的稳定性远不如PRT,并且其电阻-温度关系呈高度非线性,难以在宽温区内进行精确拟合。因此,NTC非常适合用于控制回路和差分温度测量等对绝对精度要求不高但对灵敏度和响应速度要求很高的场合。
下一篇:晶体材料的强化机制解析


 首页
首页
 检测领域
检测领域
 服务项目
服务项目
 咨询报价
咨询报价