材料的动态加载：测试方法与机理分析

当加载或变形速度远超准静态条件时，我们便进入了动态加载的范畴。在材料科学与工程领域，理解材料在动态载荷下的响应至关重要，它直接关系到结构在冲击、碰撞或地震等极端事件中的安全性和可靠性。动态加载的评估主要涵盖三类关键测试：高速拉伸或压缩试验、冲击试验以及疲劳试验。本文将对这三种方法进行深入剖析。

高速拉伸与压缩试验

高速率应变测试旨在捕获材料在快速变形下的真实力学行为。常用的试验方法包括分离式霍普金森压杆（Split Hopkinson Pressure Bar, SHPB）、单杆法、力敏块式测试仪以及伺服液压加载机等。其中，应用最为广泛的是霍普金森分离杆法，该技术可实现拉伸或压缩两种模式下的冲击变形。

其基本原理如 图1 所示，试样被夹持在输入杆与输出杆之间。为避免应力波在试样中发生复杂的反射，试样的标距长度必须足够短。图2 展示了在 2×10³ s^-1 的高应变速率下测得的流变曲线。可以观察到，与降低试验温度的效果类似，高加载速率会显著提高材料的流变应力。

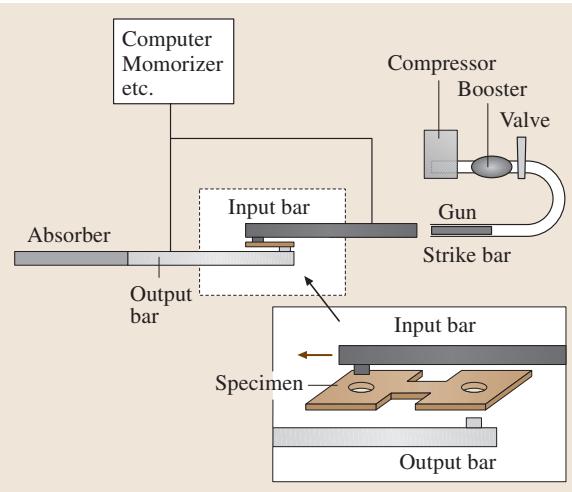
图1 基于霍普金森分离杆法的高速拉伸试验示意图

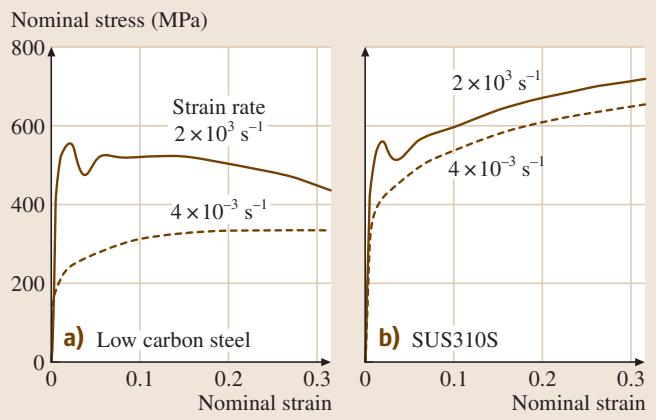
图2 高速变形（霍普金森分离杆拉伸试验）下的流变曲线：(a) 低碳钢 (b) 奥氏体钢

极高速度的变形过程近似于一个绝热过程，塑性变形产生的功会转化为热量，导致试样温度升高。对于流变应力具有较强温度依赖性的材料，如低碳钢，这种温升效应会削弱其加工硬化能力。这种独特的加工硬化行为，是高应变速率下室温变形与低应变速率下低温变形的核心区别。这些数据对于汽车的碰撞安全设计以及建筑等基础设施的抗震设计具有不可或缺的指导价值。

塑性变形过程中演化出的位错结构，也强烈依赖于试验温度和应变速率。如 图3 所示，对于低碳钢，在室温和低应变速率下变形时，会形成典型的位错胞结构。然而，在低温低应变速率或室温高应变速率条件下，观察到的则是平面位错阵列。那么，这两种路径在微观结构上究竟带来了何种差异？这正是高速力学行为研究的核心问题之一。

图3 铁素体钢拉伸变形（10%）后的位错结构：(a) 77K, 3.3×10^-3s^-1 (b) 295K, 2×10³s^-1 © 295K, 3.3×10^-3s^-1

冲击试验

冲击试验的目的是评估材料的韧性，即其在断裂前吸收能量的能力。加载方式多样，包括拉伸、压缩、弯曲和扭转。其中，最典型的当属采用三点弯曲模式的夏比（Charpy）冲击试验。如 图4 所示，试验时，一个摆锤下落并冲击一个矩形截面试样。对于韧性材料，通常会预制一个V型或U型缺口，以通过应力集中效应引导断裂。而对于陶瓷、铸铁等脆性材料，则无需引入缺口。

通过比较摆锤在冲击试样前后的势能差，可以计算出试样弯曲和断裂过程中所吸收的能量，以此量度其抗断裂能力。标准的金属材料冲击试验机可提供约300J的能量，而用于树脂或塑料的则为3J左右。另一种典型的设备是艾氏（Izod）冲击试验机，但目前已较少使用，其试样夹持方式与夏比试验不同（见 图4）。吸收能量 K 可通过以下公式计算：

K = WR(cosβ - cosα)

其中，W 是摆锤的重量，R 是摆臂的长度，α 和 β 分别是摆锤的起始角度和冲击后的最大摆起角度。

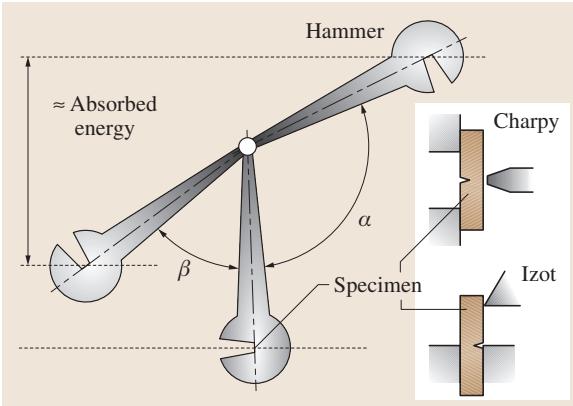
图4 冲击试验概要：夏比（Charpy）与艾氏（Izot）试验

一个有趣的现象是，某些在准静态测试中表现出韧性断裂的材料，在冲击载荷下却会发生脆性断裂。由于断裂模式对温度极为敏感，夏比冲击试验通常会在一系列不同温度下进行。将吸收的能量作为测试温度的函数绘制成图，便可得到如 图5 所示的曲线。以铁素体钢为例，吸收功会在某个特定温度区间发生急剧变化，该温度即为韧脆转变温度（Ductile-to-Brittle Transition Temperature, DBTT）。在较高温度下，试样发生韧性断裂，断口呈现典型的韧窝形貌。而在较低温度下，则观察到穿晶的解理面或晶间断裂面。DBTT的确定，既可以依据吸收功的大小，也可以通过断口上韧窝区域的百分比来判断。

冲击试验的结果是材料筛选的重要依据，但其数据很难直接用于机械设计的定量计算，例如确定设计应力。要获得定量的断裂抗性参数，则需依赖于基于断裂力学、使用预制裂纹试样的其他测试方法。

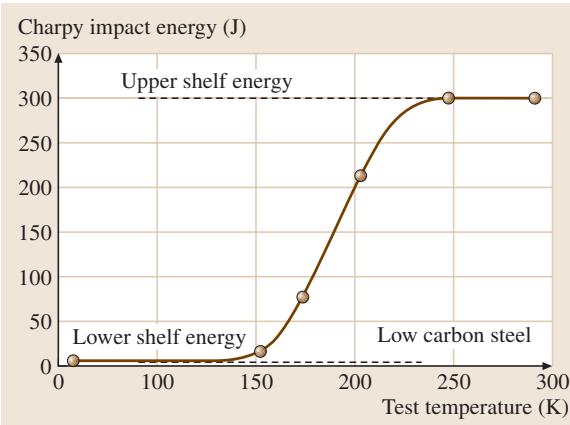
图5 夏比冲击试验观察到的韧脆转变行为

疲劳

疲劳是指材料在远低于其静态抗拉强度的循环应力作用下发生的断裂。迄今为止，已有多种疲劳测试方法被开发和应用。

旋转弯曲（四点弯曲）试验常被用来模拟车轴等部件的受力状态，其表面会承受反复的拉压应力波。试验结果通常被汇总在应力幅-断裂循环次数图（S-N曲线）中。如 图6 所示，施加的应力幅被绘制为失效循环次数的函数。在初始阶段，两者关系在对数坐标下近似线性，当循环次数达到 10⁶ - 10⁷ 左右时，曲线趋于水平，对应的应力水平被称为疲劳强度或疲劳极限 σ_w。在高于 σ_w 的应力下，材料的寿命由具体的循环周次决定，称为疲劳寿命。因此，疲劳强度和疲劳寿命是机械或结构设计的关键参数。

近期的超长寿命疲劳研究表明，某些材料即使在低于传统疲劳极限 σ_w 的应力下，经过极长时间的循环也可能发生断裂。对于老化的材料，这一点尤其需要纳入考量。

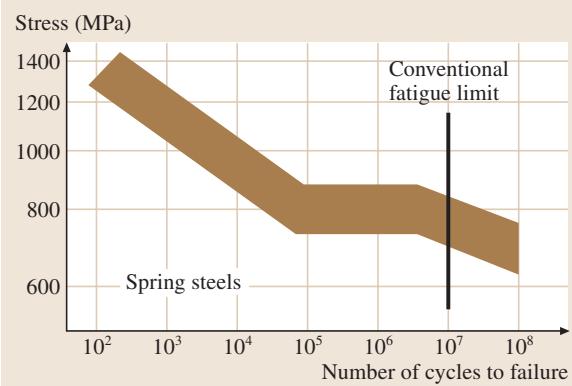
图6 疲劳断裂的应力幅-失效循环次数（S-N）曲线

平均应力对疲劳强度的影响可以通过 图7 所示的疲劳极限图来讨论。该图将 10⁷ 次循环下的应力幅绘制为平均应力的函数。构建此图时，需综合考虑材料的屈服强度 σ_s、抗拉强度 σ_B 以及通过拉伸试验（可视为四分之一疲劳循环）得到的真实断裂强度 σ_f。图中的阴影区域被评估为既能避免疲劳断裂，又能防止宏观屈服（弹性失效）的安全工作区。

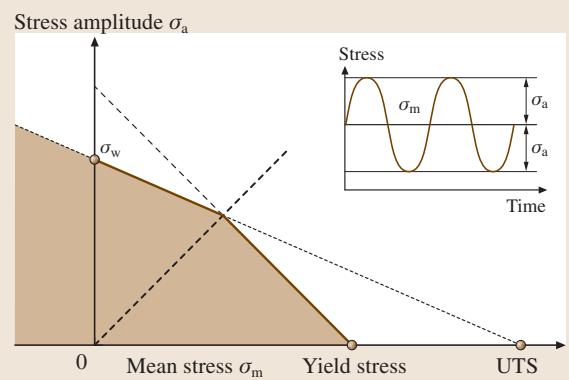
图7 考虑平均应力影响的疲劳极限图

疲劳断裂的机理可由 图8 示意。通常，疲劳裂纹萌生于材料表面或应力集中区域，如缺陷、脆性夹杂物等。若材料近乎无缺陷，滑移变形会优先在表层发生。在低于屈服强度的循环载荷作用下，局部滑移反复进行，导致表面形成微观的“侵入”和“挤出”。“侵入”可视为一种微裂纹，造成应力集中（疲劳裂纹萌生的第一阶段），并诱发裂纹尖端的局部塑性流动。随后，裂纹的扩展方向会从沿最大切应力方向转为垂直于拉应力方向，这个裂纹扩展区被称为第二阶段。

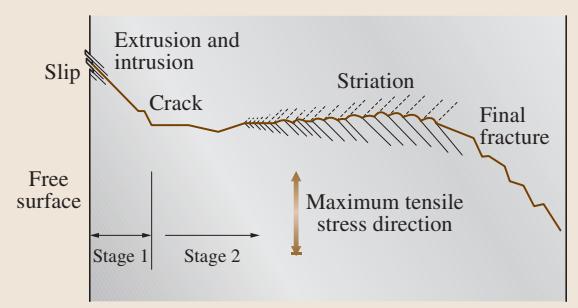
图8 疲劳断裂示意图：裂纹萌生、扩展与最终断裂

当裂纹长度增长到足以满足断裂力学给出的最终断裂条件时，瞬时断裂便会发生。该条件可表示为：

K_max ≥ K_th^F

其中，不等式左侧是最大应力强度因子 K_max (= ασ_max√πc)，α 是与试样几何相关的常数，σ_max 是施加的最大应力，c 是裂纹长度。右侧的 K_th^F 则是材料的抗疲劳断裂韧性。

第二阶段的裂纹扩展速率可以通过使用预制了尖锐缺口的试样来测量。在循环应力作用下，测量裂纹长度的变化，然后将扩展速率绘制为应力强度因子幅值 ΔK (= Δσ√πc) 的函数，如 图9 所示。在低 ΔK 区域，可通过连续减小 Δσ 来测量扩展速率。工程上，将裂纹扩展的下限定义为阈值应力强度因子 ΔK_th，该参数对材料的微观结构十分敏感。在曲线的中段，扩展行为可以用帕里斯（Paris）方程描述的线性关系来近似：

dc/dN = C(ΔK)^m

式中 C 和 m 均为材料常数。值得注意的是，第二阶段的裂纹扩展速率对微观结构不敏感。

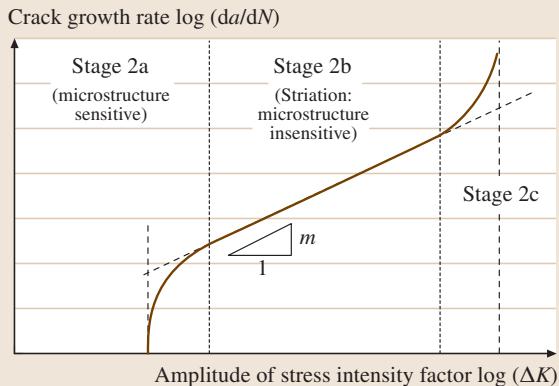
图9 疲劳裂纹扩展速率与应力强度因子幅值的关系

如果材料中初始裂纹的长度 c_i 已知（例如通过X射线透射等无损检测方法获得），那么结合上述的断裂条件和帕里斯方程，就可以预测材料的疲劳寿命 N_f。通过对帕里斯方程进行积分，我们得到：

N_f = ∫_ci^c_f [dc / C(αΔσ√πc)^m]

其中，最终裂纹长度 c_f 可由断裂条件 K_max ≥ K_th^F 计算得出。对于韧性材料，第二阶段的断裂面上会形成由循环加载引起的疲劳辉纹。因此，通过断口分析也可以反推裂纹的扩展速率。

获取精确的材料动态力学性能数据，尤其是进行复杂的疲劳寿命预测和失效分析，对试验条件控制和数据解读能力提出了极高要求。这正是专业检测实验室的核心价值所在。 精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测材料动态力学性能、疲劳与断裂分析，可靠准确。欢迎沟通交流，电话19939716636