材料准静态加载强度：从拉伸试验到多轴应力状态的全面解析

根据加载速率的不同，材料力学性能测试可分为准静态（或简称静态）测试与动态测试。在工程领域，准静态加载下的强度是衡量材料性能最基础、最核心的指标之一，其中，拉伸试验无疑是应用最广泛的手段。然而，当我们谈论材料的“强度”时，其内涵并非单一，必须厘清其在不同语境下的三种核心意义，以免混淆。

其一，当外加载荷较小时，材料的变形是可逆的，即处于弹性变形阶段。在此阶段，应力与应变成正比，遵循经典的胡克定律。拉伸应力与拉伸应变之间的斜率，即为杨氏模量（Young’s Modulus）。高杨氏模量的材料，我们称之为高刚度材料，意味着其抵抗弹性变形的能力强。

其二，当应力超过某一阈值，材料开始发生不可逆的塑性变形。塑性流动开始时的临界应力被称为屈服强度（Yield Strength），它与杨氏模量没有直接关联，表征的是材料抵抗塑性变形的能力。在工程设计中，如何精确定义屈服强度至关重要，通常采用0.2%残余应变对应的规定塑性延伸强度（Proof Stress）或下屈服强度作为评判标准。

其三，材料在应力作用下最终会发生断裂。由于断裂机制的多样性，抵抗断裂的强度（断裂强度）又不同于屈服强度。延性材料在经历显著的加工硬化和塑性失稳（如拉伸过程中的颈缩）后，通常呈现韧窝断裂。而脆性材料则几乎不发生塑性变形，直接发生脆性断裂，其抵抗脆性断裂的能力是强度的另一重要维度。此外，材料的断裂行为也受化学环境的显著影响。

拉伸试验

拉伸试验通常在室温下进行，应变速率控制在10^-4 ~ 10^-1 s^-1的范围内。试验流程、试样形状和尺寸需根据所测试的材料与产品，遵循ISO或其他相关标准。加载速率，即拉伸速率，应通过齿轮驱动或伺服液压式试验机精确控制在上述应变速率区间内。试验过程中，需要同步记录施加的载荷以及试样标距段的位移，从而得到载荷-位移图。该图可进一步转换为工程应力-应变曲线，有时甚至需要转换为真实应力-应变曲线。通过拉伸试验，我们可以获取一系列关键的力学性能参数，如屈服强度、抗拉强度、均匀伸长率、总伸长率、加工硬化指数（n值）、塑性应变比（r值）等。

延性材料的应力-应变曲线

标准拉伸试样的形貌及宏观变形行为如图1所示。试验中，根据需求，可使用应变片或引伸计监测标距长度的变化（ΔL），同时通过力传感器测量载荷（F）。基于试样的初始横截面积（A₀）和初始标距（L₀），可由下列公式计算出工程应力（σ）和工程应变（ε）：

σ = F / A₀ ε = ΔL / L₀

其中，σ的单位是Pa（即N/m²），ε为无量纲。

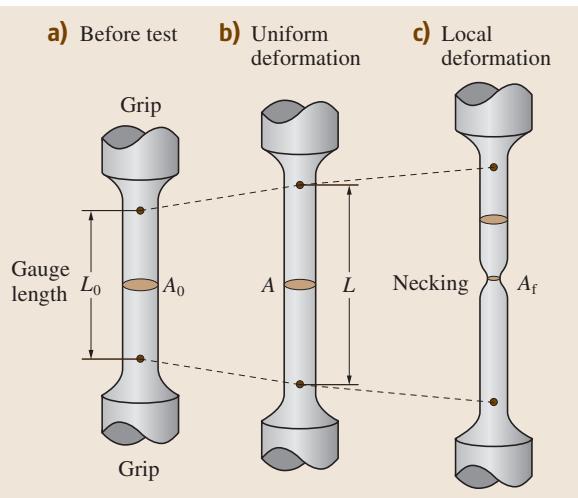图1 拉伸试样及宏观拉伸变形行为

图2展示了两种典型的工程应力-应变曲线：(a) 具有不连续屈服现象的曲线，和 (b) 具有连续屈服现象的曲线。大多数金属及合金材料呈现出(b)所示的连续屈服行为，而广泛使用的退火低碳钢则表现为(a)所示的不连续屈服。这些曲线清晰地展示了材料受力过程的三个主要区域：

1. 线弹性区：曲线初始阶段的线性部分。在此区域，应力与应变成正比，变形是完全可逆的。
2. 塑性变形区：当应力超过弹性极限，曲线偏离直线，材料进入塑性流动阶段。随着应变的增加，流动应力不断提高，这种现象称为加工硬化（Work-hardening）。此时若卸载，只有弹性应变能够恢复，而永久性的塑性应变则保留下来。在这一区域，塑性变形在整个标距段内是均匀发生的。通常假设塑性变形过程体积不变。
3. 颈缩与断裂区：当应力达到最大值，即抗拉强度（UTS或TS）后，材料发生局部塑性失稳，即颈缩现象（如图1©所示）。此时，维持材料继续变形所需的应力开始下降。颈缩发生后，变形集中于颈缩区域，此处的应力状态也从单轴拉伸转变为复杂的三轴应力状态。微孔在颈缩区中心形成、长大并相互连接，最终导致外围环状区域发生滑移分离，形成杯锥状（Cup-and-cone）断口。这是典型的延性断裂特征，其内部平坦区域由大量韧窝构成（如图3(a)所示）。

对于陶瓷等脆性材料，则观察不到颈缩现象。其流动曲线在达到断裂应力时便戛然而止，断裂通常发生在弹性变形阶段内。这类材料的断口形貌多为解理或穿晶断裂面（如图3(b)和3©所示）。

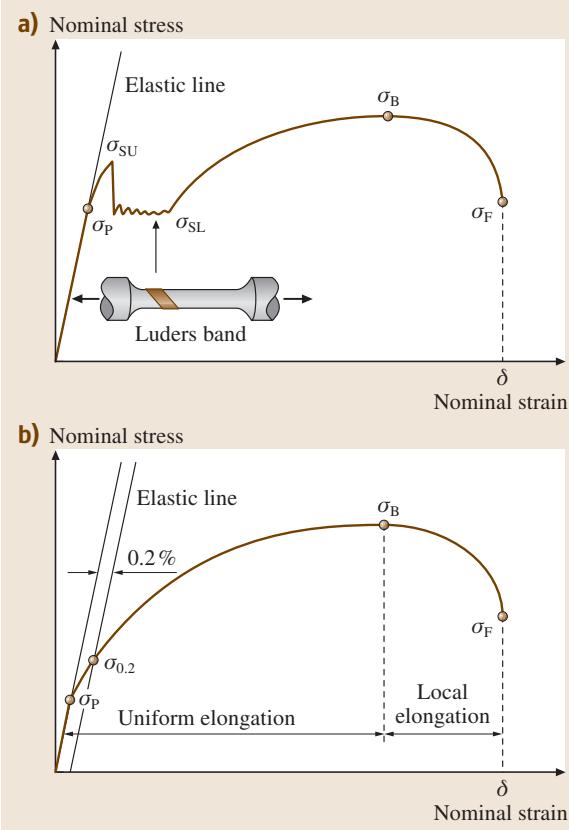图2 工程应力-应变曲线：(a) 不连续屈服 和 (b) 连续屈服

图3 断口形貌：(a) 韧窝断口, (b) 解理断口 和 © 沿晶断口

真实应力-应变曲线与加工硬化指数（n值）

在图2所示的均匀伸长阶段，塑性变形体积不变的假设近似成立。这意味着在拉伸过程中，试样标距段的横截面积（A）会随着伸长的增加而减小。因此，单位面积上承受的真实应力（σ*）应由下式给出，而非工程应力公式：

σ* = F / A

同样地，标距长度也在持续变化。因此，真实应变（ε*）被定义为：

ε* = ∫_l0^l dl / l = ln(l / l₀)

使用真实应变的一个优点是其具有可加性。例如，当长度从L_A变到L_B，再变到L_C时，从L_A到L_B的真实应变为ln(L_B/L_A)，从L_B到L_C的真实应变为ln(L_C/L_B)。两者之和ln(L_B/L_A) + ln(L_C/L_B) = ln(L_C/L_A)，等于从L_A到L_C的总真实应变。相比之下，工程应变不具备此特性。

基于体积不变假设（A₀L₀ = AL），我们可以建立工程应力/应变与真实应力/应变之间的转换关系：

σ* = σ(1 + ε) ε* = ln(1 + ε)

颈缩开始后，试样的几何形状和应力状态都变得复杂。如图1©和图4所示，颈缩区域的应力状态为复杂的三轴应力。根据Bridgman的分析，最小横截面处的拉伸应力（σ₀）可由下式给出：

σ₀ = (F / A) / [(1 + 2R / a)ln(1 + a / 2R)]

其中R和a的定义见图4。正是在这种三轴应力作用下，微孔在颈缩区中心形成，最终导致杯锥状断裂。

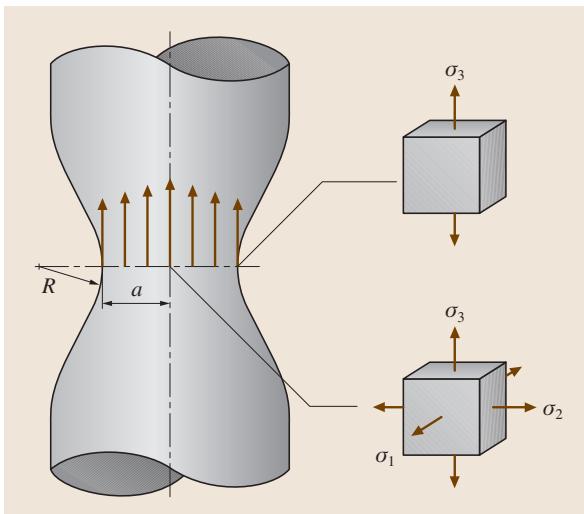图4 拉伸试验中颈缩区域的应力状态

图5展示了由工程应力-应变曲线转换得到的真实应力-应变曲线。该曲线表明，即使在发生局部变形后，材料的加工硬化仍在继续。颈缩的发生，本质上是横截面积减小导致的承载能力下降与加工硬化带来的强度提升之间相互竞争与平衡的结果。因此，真实应力（σ*）曲线与加工硬化率（dσ*/dε*）曲线的交点，即标志着颈缩的开始（见图5）。

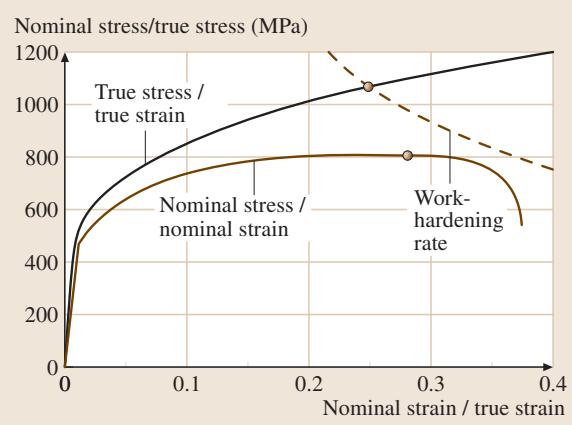图5 真实应力-应变曲线，图中绘制了加工硬化率以标示颈缩起始点

从拉伸试验中获取的关键性能参数

拉伸试验操作简便，却能提供极其丰富的材料力学性能信息，是理解材料力学行为最基础、最通用的方法。以下是几个关键的工程应用参数。

弹性极限与比例极限

绝大多数机械产品被设计在弹性变形范围内服役。弹性变形的严格界限由应力-应变曲线上的比例极限或弹性极限确定。比例极限是应力-应变关系偏离线性的点，而弹性极限则是在卸载后不产生永久变形的最大应力。这两个值的测定对所用应变测量方法的灵敏度非常敏感。在线弹性区域内，曲线的斜率即为杨氏模量（E），而横向应变与拉伸应变之比的绝对值则为泊松比（ν）。若以x₃为拉伸方向，则：

E = σ₃₃ / ε₃₃ ν = |ε₁₁ / ε₃₃| = |ε₂₂ / ε₃₃|

以钢材为例，其E值约为200 GPa，ν值约为0.3。钢的弹性应变通常小于1%，远小于其10%量级的均匀伸长率。需要强调的是，体积不变假设不适用于弹性变形。

屈服强度 (YS)

由于测量小于0.01的弹性应变需要应变片等特殊测量手段，因此在常规拉伸试验中，工程设计所用的屈服强度（YS）有特定的确定方法。对于图2(a)中低碳钢所表现出的不连续屈服，曲线上出现的上、下屈服点可直接用作工程屈服强度。由于上屈服点对拉伸速率非常敏感，因此下屈服强度应用更为普遍。在上屈服点之后，被称为吕德斯带的塑性变形区会在下屈服应力下扩展至整个试样标距段，此过程中的应变称为吕德斯伸长。

对于图2(b)中铝合金、奥氏体不锈钢等材料常见的连续屈服行为，通常采用规定塑性延伸强度，即0.2%的残余塑性应变所对应的应力值。其确定方法是在应力-应变曲线上，从横坐标0.2%应变点作弹性直线的平行线，该平行线与曲线的交点即为0.2%规定塑性延伸强度。这标志着宏观屈服的发生。尽管0.2%是工程上的通用选择，但在某些工业领域也会采用0.1%等其他标准。

抗拉强度 (TS)

图2中应力-应变曲线上的最高点对应的应力值即为抗拉强度（TS），也常被称为极限抗拉强度（UTS）。在允许发生塑性流动的极限设计中，抗拉强度被用作设计强度。

延性

描述材料延性的参数包括均匀伸长率、总伸长率和断面收缩率。均匀伸长率对应于抗拉强度点的应变，对冲压成形等塑性加工工艺至关重要。超过抗拉强度点后，材料开始发生颈缩。总伸长率则是指材料断裂时的总应变。总伸长率的值与所采用的标距长度有关。因此，有时也使用断裂应变（ε_f），定义为ε_f = ln(A₀ / A_f)，其中A_f是断裂后颈缩区的最小横截面积。传统上更常用断面收缩率（φ），定义为φ = [(A₀ - A_f) / A₀] × 100%。纯金属的极端情况是断裂成一个点，此时A_f = 0。

加工硬化指数 (n值)

图5所示的真实应力-应变曲线常可用Hollomon方程进行拟合：

σ* = K(ε*)ⁿ

其中，K为强化系数，n为加工硬化指数。通过选取两个测量点或对lnσ与lnε在适当应变范围内进行最小二乘法拟合，即可确定K和n值。n值是一个非常重要的参数，因为它与均匀伸长率直接相关。塑性失稳条件，即颈缩的起始点，可由下式给出：

dF = σdA + Adσ = 0

在体积不变的假设下，该方程可改写为σ* = dσ*/dε*，由此可得ε* = n。这意味着，加工硬化指数n值在数值上等于均匀塑性变形的真实应变。一个大的n值意味着材料具有优异的塑性成形能力。

准确测定材料的拉伸性能，包括加工硬化指数等关键参数，对于产品设计和质量控制至关重要。这不仅要求试验设备精度高，更需要对试验标准和数据解读有深刻的理解。这正是专业检测实验室的核心价值所在。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测金属材料拉伸性能，可靠准确。欢迎沟通交流，电话19939716636

兰克福德值 (塑性各向异性：r值)

另一个表征塑性成形性，同样通过拉伸试验获得的重要参数是r值，主要用于评价薄板金属材料。当拉伸应变达到10-20%时，测量试样的宽度应变（ε_w）和厚度应变（ε_t），r值由下式确定：

r = ε_w / ε_t

若采用体积不变假设，上式可变为：

r = ln(W₀ / W) / ln(LW / L₀W₀)

其中W₀、L₀和W、L分别代表拉伸试验前后的宽度和标距长度。对于薄板材料，精确测量宽度和长度远比测量厚度容易。对于各向同性材料，r值为1。然而，由于织构的存在，市售的工程材料在塑性流动中通常表现出各向异性。高r值的材料在深冲等加工过程中厚度减薄较小，因此备受青睐。为了获得高r值，精确的织构控制技术是关键。

压缩试验

压缩试验看似是拉伸试验的逆过程，但要获得可靠的应力-应变曲线，需要更高的试验技巧。图6展示了圆柱体压缩的示意图。试样的顶面和底面必须保持良好的平行度。试样与压头之间的摩擦必须通过石墨或MoS₂粉末等合适的润滑剂降至最低，否则如图6(b)所示的“鼓形”效应会变得严重，导致约束变形。如果压缩对中不佳，试样在很小的应变下就容易发生屈曲或弯曲。为避免屈曲，试样的长度与横截面积之比需要精心设计，通常直径（d₀）与高度（h₀）之比选在1.0-3.0之间。

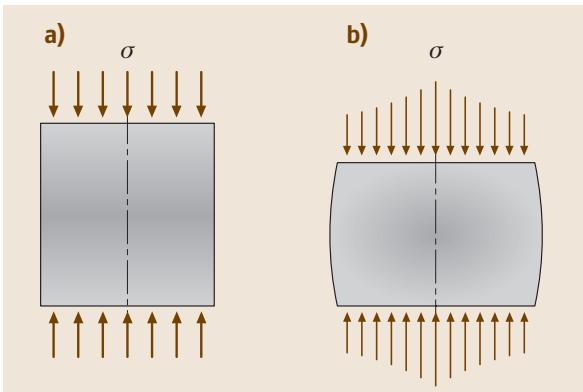图6 压缩试验及鼓形效应示意图

压缩试验得到的工程应力-应变曲线通常高于拉伸试验曲线，因为压缩过程中横截面积是增大的。因此，比较拉伸与压缩行为时，必须使用真实应力-应变曲线。如果材料是塑性各向同性的，那么如图7所示，两条真实应力-应变曲线应该重合。然而，如果材料中存在相或晶间残余应力（所谓的第二类残余应力），其压缩和拉伸的屈服强度会不同，这种现象被称为强度差异（SD）效应。

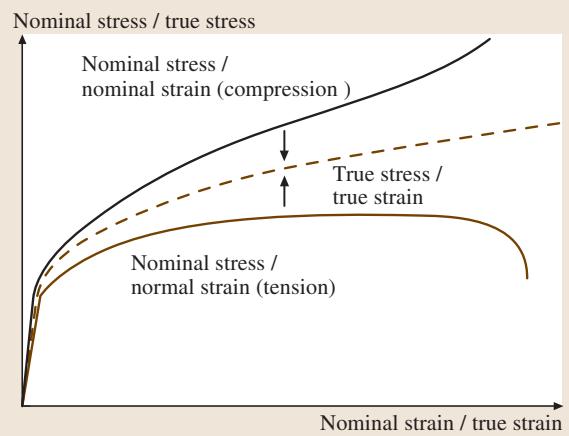图7 压缩与拉伸流动曲线的比较

一般而言，如图8所示，经过一定量的拉伸塑性变形后，材料在反向压缩时的流动应力（真实应力）会低于继续拉伸时的流动应力。这种现象被称为包申格效应（Bauschinger Effect, BE）。包申格效应的大小通常用BE应力或BE应变来量化。当应变路径改变时，即使在双轴或三轴应力状态下，流动应力也会降低。在应力空间中，屈服条件由一个屈服面来描述。材料经过塑性变形（加工硬化）后，屈服面会扩大并在应力空间中移动。这种移动可以是均匀扩大的各向同性硬化，也可以是屈服面形状大小不变、仅在应力空间中平移的随动硬化。包申格效应是理解零件塑性成形过程的关键，并且与材料的低周疲劳行为密切相关。

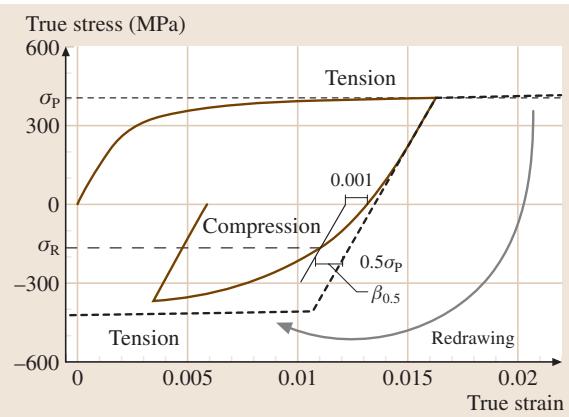图8 用于检验包申格效应（BE）的拉伸-压缩试验

硬度试验及其与强度的关系

硬度测试本质上是一种利用压头进行的局部压缩试验。压头由金刚石或高碳马氏体钢等高硬度材料制成。如图9所示，将压头压入被测材料表面，卸载后测量压痕尺寸。维氏硬度试验采用金字塔形金刚石压头，其压痕面积与施加载荷近似成正比，这意味着维氏硬度值对载荷不敏感。

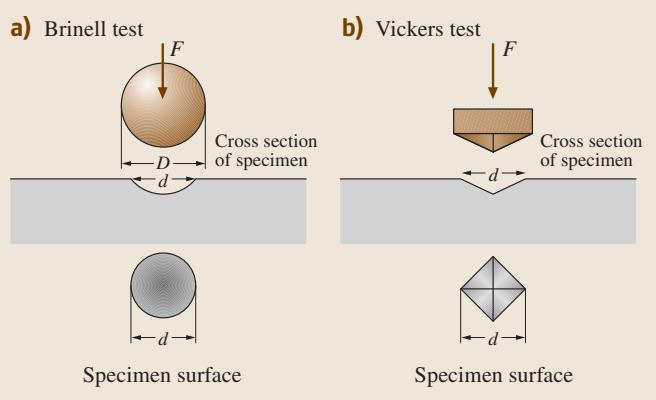图9 压痕法硬度试验

根据弹塑性分析，压痕下方塑性区的代表性塑性应变约为8%，因此硬度值应对应于简单拉伸或压缩试验中8%应变时的流动应力。图10显示了硬度与拉伸性能（屈服强度或抗拉强度）之间的关系，两者表现出极好的一致性。经验关系式 HV ≈ cY（其中系数c约为2.9-3.0）常被用来将维氏硬度（HV）与屈服或抗拉强度（Y）关联起来。因此，硬度测试是快速评估材料强度，尤其是工程产品强度的便捷方法。

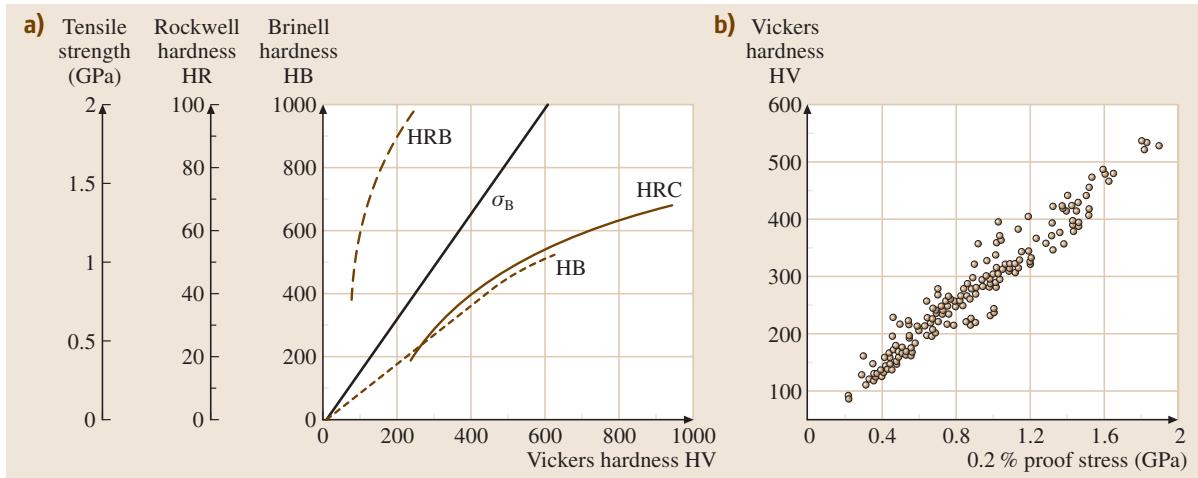图10 硬度与拉伸性能的关系

随着纳米硬度技术的发展，我们可以在更微观的尺度上探究强化机制。例如，图11展示了对回火马氏体钢在宽载荷范围内进行硬度测试的应用。工程材料常具有多尺度的非均匀微观结构，导致多尺度的非均匀塑性变形。回火马氏体由板条、块和包等结构单元组成，其强化机制是晶粒细化、位错密度、固溶碳和碳化物沉淀等多种因素的叠加。通过使用不同载荷范围的硬度计进行测试，可以如图11(b)所示，分离出不同强化机制的贡献。

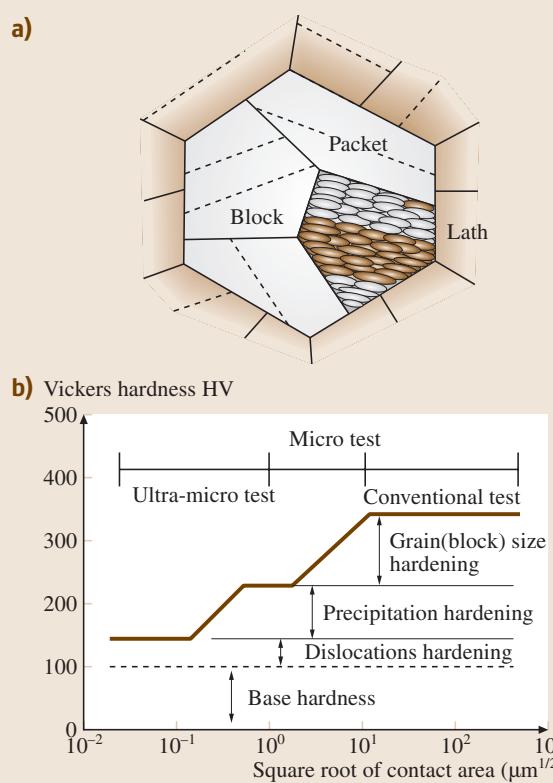图11 使用不同载荷的硬度测试研究回火马氏体钢的强化机制

弯曲试验

弯曲试验的示意图如图12所示，常用于测量脆性材料的强度或延性材料的弯曲成形性。试验分为三点弯曲和四点弯曲两种。三点弯曲操作简单，但四点弯曲更受青睐，因为它能在试样中心区域产生恒定的弯矩M。如图12(a)所示，当矩形试样弯曲时，其横截面上会产生应力应变分布，上表面受压，下表面受拉，中间存在一个应力为零的中性面。在弹性变形阶段，应变ε与曲率半径ρ的关系为：

ε = y / ρ

应力与应变成正比，最大应力σ可通过下式计算：

σ = 6M / (bh²)

其中b和h分别为试样的宽度和厚度。弹性阶段的应力分布如图12(b)所示。当弯矩M达到屈服弯矩M = σ_sbh²/6后（σ_s为屈服强度），应力分布从图12(b)向图12©转变，塑性区从中性面向外扩展。

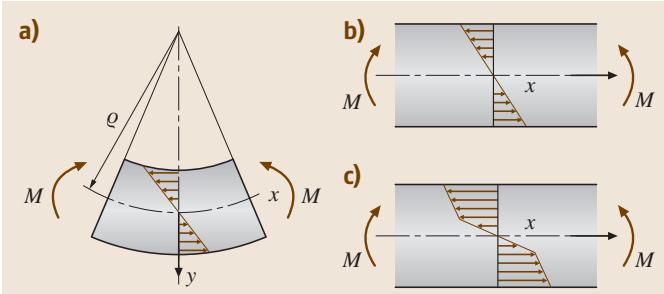图12 弯曲试验：(a) 变形示意图, (b) 弹性变形应力分布, © 弹塑性变形应力分布

扭转试验

剪切变形可视为拉伸与压缩双轴变形的组合。扭转试验尤其适用于线材和棒材。图13展示了扭转试验的示意图（a）以及圆棒横截面上的切应力分布（b）。工程切应变γ与扭转角θ和棒长L相关：

γ = rθ / L

考虑应力平衡，扭矩T产生的最大切应力τ为：

τ = 16T / (πd³)

其中d为圆棒直径。与弯曲试验类似，屈服后应力分布会发生变化，如图13©所示。

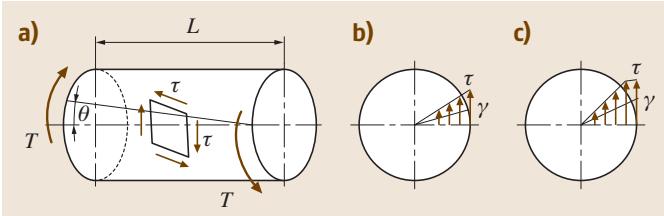图13 扭转试验：(a) 变形示意图, (b) 弹性变形应力分布, © 弹塑性变形应力分布

多轴应力下的屈服准则

拉伸和压缩试验是在单轴加载下进行的。然而，实际工况通常是复杂的三轴应力状态，可用一个包含六个分量的应力张量来描述。通过坐标变换，可以找到一个主应力坐标系，使得所有切应力分量为零，只剩下三个主应力σ₁, σ₂, σ₃。

在一般应力条件下，最常用的两个屈服准则是Tresca准则和von Mises准则。

• Tresca准则（最大切应力理论）：认为当最大主应力与最小主应力之差达到某一临界值时，材料开始屈服。即 |σ₃ - σ₁| = 2k = σ_s。
• von Mises准则（形状改变比能理论）：认为当单位体积的畸变能达到临界值时，材料开始屈服。该准则可表示为： [(σ₁ - σ₂)² + (σ₂ - σ₃)² + (σ₃ - σ₁)²] = 2σ_s²

通常，材料的实际屈服行为介于这两个准则之间。为了方便工程应用，通常将一般应力状态投影到单轴拉伸的情况，计算出一个等效应力（σ_eq）。根据von Mises准则，等效应力为： σ_eq = {[(σ₁ - σ₂)² + (σ₂ - σ₃)² + (σ₃ - σ₁)²] / 2}^1/2

图14展示了在拉伸与扭转复合加载下的屈服面。

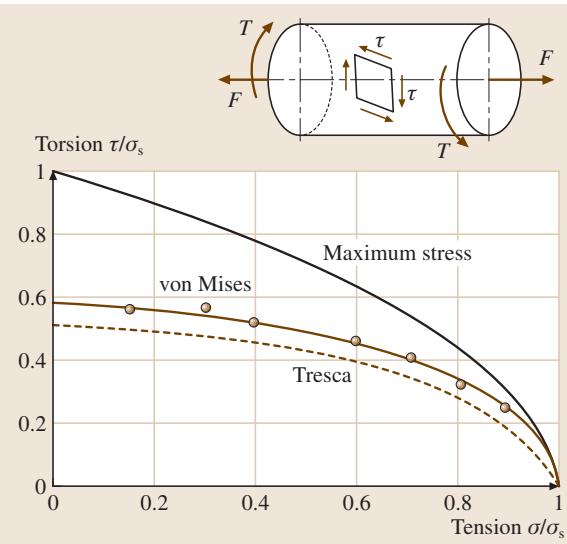图14 拉伸与扭转复合应力下的屈服面

蠕变试验

塑性变形和断裂通常表现出时间依赖性。当外加载荷保持恒定时，试样会随时间缓慢地发生塑性变形，这种现象称为蠕变。蠕变在高温下（T > 0.3T_m，T_m为材料熔点）尤为显著。如图15所示，恒温恒载下的蠕变曲线通常分为三个阶段：

1. 瞬态蠕变（第一阶段）：加载后，应变速率随时间逐渐减小。
2. 稳态蠕变（第二阶段）：蠕变速率达到一个近似恒定的最小值。
3. 加速蠕变（第三阶段）：蠕变速率急剧增加，最终导致试样断裂。

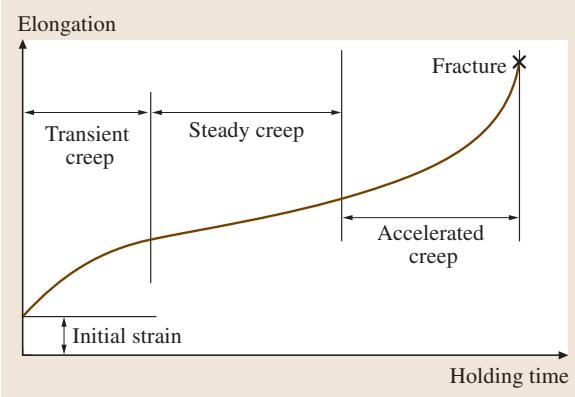图15 恒定载荷和温度下的典型蠕变变形行为

蠕变试验方法多样，包括恒应力蠕变、扭转蠕变、拉扭复合蠕变等。为了将在不同温度下获得的蠕变数据进行整合，常使用Larson-Miller参数：

λ = T(20 + log t_r) × 10^-3

其中t_r为断裂时间。通过该参数，可以将不同温度下的应力-断裂时间数据很好地汇总到一条σ-λ主曲线上。

应力松弛

塑性变形的时间依赖性还体现在应力松弛现象上。当试样被拉伸到一定应变（进入塑性区）并保持总应变恒定时，随着时间的推移，部分弹性应变会转化为塑性应变，导致试样内部的应力（弹性应变）逐渐降低。测量应力松弛行为需要高灵敏度的应变检测器，因为弹性应变的变化非常微小。本质上，这是一种应变速率极低且随时间连续递减的特殊拉伸试验。