表面形貌评定的参数化方法及其统计学基础

在表面形貌的测量领域，除了直接生成表面高度扫描图的方法外，还存在一系列旨在获取可测量参数的技术。这些参数并不逐点描绘形貌，而是表征表面宏观或微观形貌的某种平均属性。其根本出发点在于，光波与表面的一切相互作用现象，都深刻地受到表面微观几何结构的影响。基于这一原理，技术人员发展出了依赖镜面/漫反射、散斑及偏振等光学现象的测量方法。

所谓的积分法（integral methods），正是这一思路的集中体现。它将表面粗糙度作为一个整体进行测量和量化，其操作核心是建立在表面统计学、相关性分析和频域分析之上的一系列参数。这种统计性描述的最大优势在于，它能用最少数量的参数来描绘一个轮廓或整个表面的核心特征，从而实现高效、精炼的表征。

对表面形貌进行统计分析，会衍生出形形色色的参数，其中很多并未被通行的ISO标准所覆盖。除了纯粹的统计量，我们还能从给定表面高度函数 h(x) 的自相关函数（ACF）和自协方差函数（ACVF）中获得更深层次的信息。对于零均值函数而言，ACF与ACVF是等同的。另一个极其重要的工具是功率谱密度函数（PSDF）。

从物理意义上讲，这些统计函数为我们提供了独特的视角：

• 功率谱密度函数 (PSDF)：它将复杂的表面轮廓分解为不同空间频率的简单正弦波的叠加，揭示了表面在不同尺度上的粗糙度分量。
• 自相关函数 (ACF)：它描述了表面轮廓上一个点与相隔一定距离的另一点之间的相关程度，能够有效识别表面是否存在周期性或重复性的结构。

这两个核心函数在数学上通过傅里叶变换相关联，其具体表达如下：

PSDF(k_x) = L^-1 |∫₀^L h(x)exp(-ik_xx)dx|²

ACF(τ) = L^-1 ∫₀^L h(x)h(x + τ)dx = (1/2π) ∫_-∞^∞ PSDF(k_x)exp(ik_xτ)dk_x

对粗糙表面光散射现象的简化理论处理，通常基于惠更斯-菲涅尔原理，如下图所示。

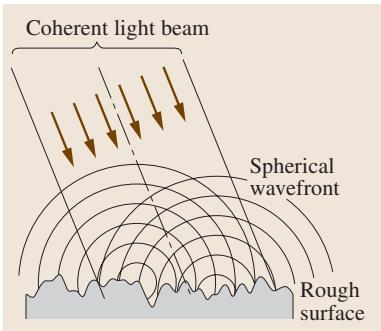
图1 惠更斯-菲涅尔原理：粗糙表面光散射现象的理论基石

在这里，有一个至关重要的观点需要强调：无论采用何种测量方法，其获得的数据必然受限于测量仪器自身的感知范围（sensing regime）。任何处于该范围之外的样品特性，仪器都无法“看到”，自然也无法体现在数据中。这就解释了一个长期困扰工程师的问题：为何两台经过最佳程序充分校准的仪器，在测量同一块样品时，其结果仍可能无法达成一致。仪器的感知能力边界（正如Stedman图所定义的那样）是无法逾越的内在限制。

这种对仪器内在限制的深刻理解，以及对复杂统计参数的精确解读，构成了高质量表面形貌分析的核心。它要求操作者不仅熟悉设备，更要洞悉其背后的物理原理与数据处理逻辑。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测表面粗糙度与形貌分析，可靠准确。欢迎沟通交流，电话19939716636

当然，除光学方法外，也存在基于电容或其他原理的参数化测量方法，但它们已超出了本章的讨论范畴。