磁共振波谱学：从基本原理到材料结构解析

磁共振波谱（Magnetic Resonance Spectroscopy, MRS）是一类基于原子核或电子自旋的磁共振现象建立的实验方法。它在固体材料的缺陷与杂质研究、分子结构分析乃至微观结构表征等领域，扮演着不可或缺的角色。

当电子和原子核具有角动量 ħS（其中 ħ 为普朗克常数）时，便会伴生一个磁矩 μ：

μ = γħS

这里的 S 代表自旋量子数，对于电子自旋，其值为 s = 1/2；对于电子轨道角动量，为 j；而对于核自旋，则为 I（通常是 1/2 的各种倍数）。系数 γ 被称为磁旋比，其定义为：

γ ≡ ge / 2mc

在此式中，g 是 g-因子（一个范围在 1-3 之间的无量纲常数，取决于角动量的来源），m 是粒子的质量，e 是电子电荷，c 是光速。

从量子力学的视角看，当一个自旋或磁矩置于强度为 B₀ 的静磁场中时，它会分裂成一系列分立的本征能态。以最简单的 S = 1/2 系统为例，自旋会分裂为两个能级，如 图1a 的能级图所示。这两个能级间的能量差为 ħωL，其中 ωL 是拉莫尔角频率：

ωL = γB₀

在磁共振实验中，样品除了承受主静磁场 B₀ 外，还会受到一个垂直于 B₀ 且频率恰好为拉莫尔频率的微弱交变磁场。这个交变场能够共振地诱导自旋在两个能级间跃迁。图1a 中实心圆的数量代表了各个能级的粒子布居数。在热平衡状态下，低能级（自旋向上）的粒子数总是多于高能级（自旋向下）的粒子数，因此，当施加共振电磁波时，自旋系统会净吸收电磁波的能量。

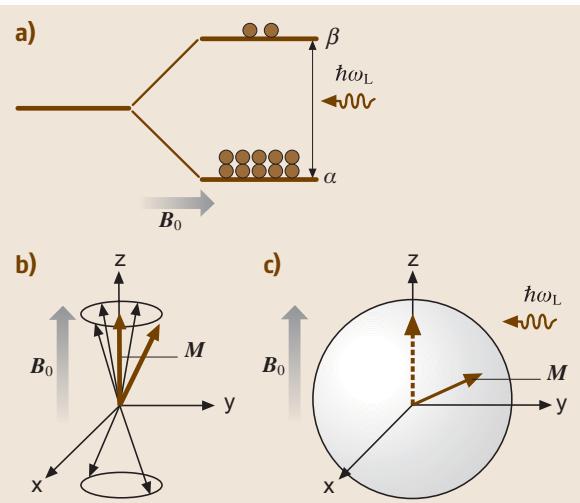
图1 a-c. 一个 S = 1/2 系统的磁共振现象的 (a) 量子力学图像与 (b), © 经典矢量模型。(a) 热平衡时，塞曼分裂的低自旋能态 α 的粒子布居数多于高能态 β，施加共振电磁波引起能级间跃迁，导致净能量吸收。(b) 经典模型中，宏观磁化强度 M 是热平衡下各个自旋磁矩随机进动的平均结果。© 发生共振时，自旋磁矩被“聚束”起来，合成的磁化矢量开始向下翻转，在真实空间中描绘出一条螺旋轨迹。

换个角度，用经典物理的矢量模型来理解，一个磁矩在静磁场中会围绕磁场方向（通常定义为 z 轴）以拉莫尔频率进行旋进，如 图1b 所示。然而，在热平衡状态下，这种旋进是无法被直接探测到的，因为每个自旋的旋进相位都是随机的（非相干的）。在包含海量自旋的宏观样品中，这些随机旋进的横向分量会相互抵消，最终只剩下因低能级布居数稍多而产生的净 z 轴磁化分量。磁共振的一个直观图像是：在共振微波的作用下，原本杂乱的自旋变得步调一致（相干），它们合成的宏观磁化矢量（如 图1c 所示）开始向下翻转，并描绘出一条螺旋线轨迹。尽管这个经典矢量模型在电子自旋共振（ESR）或电子顺磁共振（EPR）中较少使用，但它在阐释核磁共振（NMR）现象时却反复被援引。（尽管EPR和ESR在教科书中常被混用，但在本文中，ESR泛指包括EPR在内的整套方法学。）

磁共振技术之所以能提供丰富的材料结构信息，其根本在于自旋之间存在着多种来源的相互作用。这些复杂的相互作用行为，可以通过一个有效的自旋哈密顿量 H 来形式化地描述：

H = B₀γ'eS - 2SJ'eS + SA'I - B₀γnI + IJnI + IQI + ...

这里，S 和 I 分别是总电子自旋和总核自旋的量子算符。公式中的各个项分别代表了不同的物理相互作用：

• 张量磁旋比 γ'e 和 γn（或对应的张量 g-因子）描述了塞曼分裂。
• J'e 描述了电子自旋间的直接交换相互作用。
• A 描述了电子与原子核之间的超精细相互作用，它反映了自旋所处的化学环境（如各向异性的晶体场）。
• Jn 描述了核自旋间的间接相互作用。
• Q 描述了当原子核 I > 1/2 时，其电四极矩与原子核位置的电场梯度之间的核四极矩相互作用。

由于电子和原子核的质量差异巨大，导致 γ'e >> γn。这意味着，电子自旋受核自旋的影响很小，仅仅是微扰；但正是这种微扰（主要来自哈密顿量的第三项 SA'I），使得EPR谱图中呈现出信息量极大的精细结构。反之，电子自旋的存在会对核自旋状态产生巨大影响，这使得顺磁性样品的NMR谱图变得异常复杂，难以解析。

当样品中不存在电子自旋时，情况则大不相同。核自旋与环境的相互作用非常微弱，因此原子核拥有很长的自旋寿命——这个量用于描述一个建立起来的自旋相干态能在多长时间内得以维持。换言之，核自旋的寿命对原子核的动态运动极为敏感，一旦原子核开始运动（例如在固体中扩散），其自旋寿命就会缩短。NMR的这一独特性质，使其成为研究固体中杂质扩散和分子结构解析的强大工具。要精确解析这些由复杂相互作用和动态过程产生的谱图，往往需要深厚的专业知识和丰富的实践经验。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测磁共振波谱分析，可靠准确。欢迎沟通交流，电话19939716636

除了EPR和NMR，磁共振波谱学还包含一个广泛的技术家族。例如，光探测磁共振（ODMR）、磁圆偏振发射（MCPE）和磁圆二色吸收（MCDA）可以看作是EPR的光谱学版本。而μ子自旋共振（μSR）和扰动角关联（PAC）则可被视为应用于奇异粒子或放射性粒子的特殊核磁共振技术。这些衍生方法进一步拓展了磁共振技术在不同科学领域的应用边界。