解码晶体结构：从离子半径比到配位多面体的微观构筑法则

在离子晶体的微观世界中，原子并非随意堆砌，而是遵循着严谨的几何与能量最优化原则。一个中心阳离子被多少个阴离子所包围，并形成何种空间构型，这不仅是基础的化学问题，更直接决定了材料的宏观物理化学性质。这个核心参数，我们称之为配位数。

例如，在常见的氯化钠（NaCl）晶体中，每个Na⁺离子都被6个等距的Cl^-离子包围，形成一个正八面体结构。因此，Na⁺的配位数就是6。这些围绕中心阳离子、在空间上构成特定几何形态的阴离子，其中心连线所构成的多面体，即为配位多面体。配位数为4，通常对应正四面体；配位数为6，则对应正八面体。

显而易见，配位数决定了配位多面体的基本形态。那么，这个看似简单的数字背后，究竟隐藏着哪些决定性的物理化学规则？

核心法则：离子半径比的几何约束

在理想的离子晶体中，决定一个阳离子能“容纳”多少个阴离子的首要因素，是阳离子与阴离子的半径之比（r⁺/r^-）。这个比值本质上是一个空间几何问题：在维持体系稳定的前提下，一个大球周围最多能堆积多少个小球，并保证所有小球都能与中心大球紧密接触。

表1 离子半径比（r⁺/r^-）与配位数及配位多面体的关联

我们以配位数为6的八面体构型为例，推导其临界的离子半径比。当阳离子恰好能被6个相互接触的阴离子包围时，体系达到最紧密的稳定状态。取其中一个通过4个阴离子和1个阳离子中心的截面（如图1所示），可以建立如下几何关系：

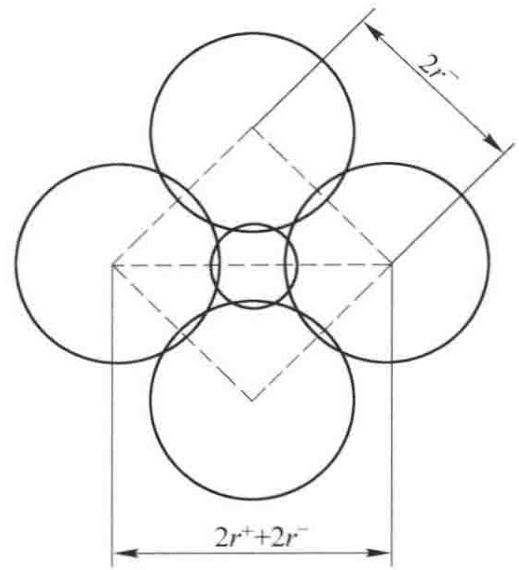图1 计算r⁺/r^-临界值的几何图解

根据勾股定理，正方形对角线长度等于边长的√2倍。图中，正方形的边长为2r^-，对角线长度为2r⁺ + 2r^-。

(2r^-)² + (2r^-)² = (2r⁺ + 2r^-)²

简化后得到：

√2 * (2r^-) = 2r⁺ + 2r^-

两边同除以2r^-，整理可得：

r⁺/r^- = √2 - 1 ≈ 1.414 - 1 = 0.414

这个0.414就是八面体配位（配位数为6）的临界半径比。当r⁺/r^-小于此值时，阳离子太小，无法同时接触6个阴离子，体系不稳定，倾向于形成更低配位数的结构（如四面体）；当大于此值时，阳离子则能稳定地填充在八面体空隙中。

回到最初的NaCl例子，已知Na⁺半径(r⁺)为0.098 nm，Cl^-半径(r^-)为0.181 nm。计算其半径比：

r⁺/r^- = 0.098 / 0.181 = 0.54

这个值恰好落在0.414 ~ 0.732的区间内，完美地解释了为何Na⁺在NaCl晶体中稳定地以6配位形式存在，形成八面体构型。这正是离子半径比法则的威力所在——它为晶体结构的稳定性提供了简洁而强大的几何判据。

深入硅酸盐体系：理论与现实的交汇

离子半径比法则是预测晶体结构的有力工具，在硅酸盐等复杂体系中同样适用。在硅酸盐晶体中，主要的阴离子是O^2- (r^- ≈ 0.132 nm)。我们可以据此预测常见阳离子的配位情况。

• Si⁴⁺：其半径 r⁺ = 0.039 nm。r⁺/r^- = 0.039 / 0.132 = 0.296。该值介于0.225 ~ 0.414之间，因此Si⁴⁺的配位数是4，形成极其稳定的[SiO₄]四面体。这是几乎所有硅酸盐矿物结构的基本骨架。
• Al³⁺：其半径 r⁺ = 0.057 nm。r⁺/r^- = 0.057 / 0.132 = 0.432。这个值非常接近0.414的临界点，理论上应为6配位（八面体）。事实上，Al³⁺确实常以6配位存在，但它也时常会取代Si⁴⁺的位置，进行4配位。
• Mg²⁺：其半径 r⁺ = 0.078 nm。r⁺/r^- = 0.078 / 0.132 = 0.59。这明确指向了6配位。然而，在某些结构（如尖晶石）中，也观察到了4配位的Mg²⁺。

在实际材料开发中，准确判断Al³⁺究竟是以四面体还是八面体配位存在，往往直接影响材料性能。如果您在实际工作中也面临类似的物相鉴定挑战，我们非常乐意与您一同探讨解决方案。

表2 硅酸盐中主要阳离子的配位数 (r_O^2- = 0.132 nm)

表3 常见阳离子与氧配位时的配位数

超越几何：影响晶体结构的深层因素

离子半径比模型为我们提供了第一层近似，但现实世界的复杂性远不止于此。当理论预测与实验观察出现偏差时，我们需要引入更深层次的因素来解释。

一个晶体结构的最终形态，可以看作是一个由多个变量决定的函数：

结构 (s) = f (组分及比例 (Σn), 离子半径 (r⁺, r^-), 极化率 (α))

1. 组分与化学计量比 (Σn)：这是最基本的决定因素。MgO (AB型) 和 SiO₂ (AB₂型) 的化学式不同，其晶体结构自然迥异。
2. 相对大小 (r⁺, r^-)：即我们讨论的离子半径比。即便化学式类型相同（如MgO和CaO均为AB型），但由于Mg²⁺ (0.078 nm) 和 Ca²⁺ (0.106 nm) 的半径不同，导致它们的配位数和晶体结构也不同。
3. 极化效应 (α)：这是修正理想离子模型的关键。当阳离子电场足够强，或阴离子本身易变形时，阴离子的电子云会被拉向阳离子，发生“极化”。这使得离子键带上了一部分共价键的成分，偏离了纯粹的静电吸引和刚性球模型。

一个经典的例子是NaCl和CuCl。两者的离子比例均为1:1，半径比也极其接近（NaCl为0.54，CuCl为0.53），理论上都应是6配位。但Cu⁺的极化能力远强于Na⁺，强烈的极化作用导致其配位数从理论的6降至实际的4。

温度和压力也会影响离子半径，进而改变配位数，但通常极化效应的影响更为显著。因此，要精确表征一种材料的真实结构，尤其是在存在多种可能构型或复杂取代的情况下，单纯的理论计算是不够的。这正是专业检测实验室的核心价值所在。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），专业的权威第三方检测机构，专业检测晶体结构分析央企背景，可靠准确。欢迎沟通交流，电话19939716636

终极体现：同质多象与性能差异

当化学组成完全相同，仅因形成时的温度、压力等条件不同而呈现出多种晶体结构时，这种现象被称为同质多象。这是上述所有影响因素综合作用的最终体现。

最著名的例子莫过于碳（C）的两种同素异形体：金刚石和石墨。前者是等轴晶系，碳原子以sp³杂化形成坚固的四面体网络，硬度极高；后者是六方晶系，碳原子以sp²杂化形成层状结构，层间作用力弱，质地柔软。

同样，SiO₂在不同温度压力下，可以形成石英、鳞石英、方石英等多种变体，每种变体都有其独特的晶体结构和物理性质。理解这些微观结构法则，不仅是材料科学的基础，更是调控材料性能、开发新材料、进行质量控制的根本依据。