对道路、桥梁及隧道等混凝土结构进行质量评估,其核心指标——如厚度、强度和弹性性能——的精确测量至关重要。传统的取芯破坏性试验方法,不仅成本高昂、耗时费力,更会对结构本身造成不可逆的损伤。因此,发展高效、可靠的无损检测(NDT)技术,一直是工程界追求的目标。超声波法,凭借其穿透性和对材料力学性能的敏感性,为此提供了极具潜力的解决方案。
然而,将超声波技术应用于混凝土并非易事。混凝土是一种典型的非均匀介质,其内部粗骨料的存在会对超声波产生强烈的声散射,严重干扰有效信号的传播与接收。这使得利用超声波精确检测混凝土厚度、评估其内部性能成为一项公认的技术难题。攻克这一难题,主要从两个方向展开:一是提升超声波换能器的性能,二是开发先进的信号处理算法,以从复杂的噪声中提取出有用的底波反射信号。
精确测量混凝土路面或支护结构的厚度,是评判工程质量的基础。面对声散射的挑战,研究人员开发了多种方法来提升检测的准确性。
对于厚度在20cm左右的混凝土,可以采用一种特殊设计的宽带窄脉冲超声波换能器。这种探头工作在厚度振动模式(即 K<sub>t</sub> >> K<sub>P</sub>),中心频率约200kHz,脉冲响应极短(约1个周期),带宽则达到约2倍频程。其核心优势在于时间分辨率高,且径向的直达波信号较弱,这使得从混凝土界面反射的回波信号更容易被识别。
检测时,采用一发一收的布置方式(如图1)。首先测定混凝土的声速 c,再测量超声波从发射到接收到界面反射回波的时间 t。混凝土的厚度 L 可通过以下几何关系计算得出:
L = 0.5 * √(c²(t - t₀)² - d²)
其中:
d:两个探头之间的距离t₀:系统的零读数或仪器延迟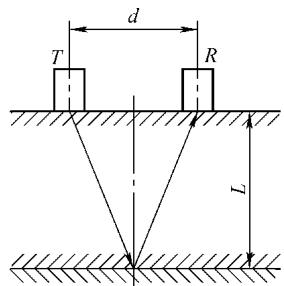
图1 窄脉冲直探头法示意图
在实际接收到的波形(如图2)中,可以清晰地分辨出发射耦合信号(E)、沿表面传播的直达波(D)以及关键的底面反射波(R)。
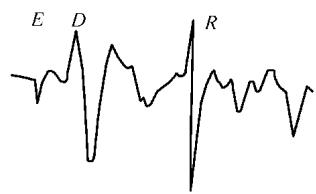
图2 窄脉冲直探头法接收波形图
当混凝土厚度超过20cm时,声散射效应愈发严重,简单的直读法难以奏效。此时,必须借助信号处理技术。脉冲相关法便是其中一种有效手段。该方法的物理基础是:尽管骨料散射具有随机性,但来自同一底面的反射波形具有高度的相似性(相关性)。
具体操作是,先从一个信号质量较好的样本中提取一个理想的底面反射波,将其作为“母波”序列。然后,将这个母波与其他实际接收到的、混杂着噪声的回波信号(子波)进行互相关运算。运算结果中,相关峰值最强的位置就对应着底面反射波的准确到达时间,从而可以计算出厚度。如图3所示,这种方法能够有效锁定底波位置,测量误差可控制在5%以内。
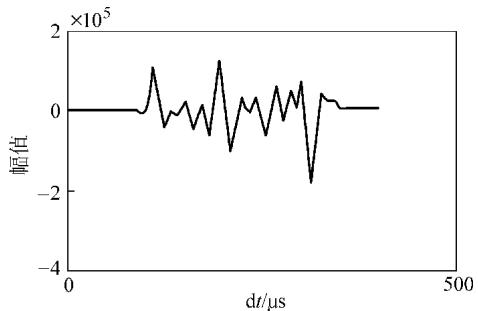
图3 互相关运算输出序列
分离谱法是另一种高级信号处理技术,其原理基于散射波和反射波在频域上的不同表现。在一个理想化的混凝土模型中(如图4),来自大量骨料的散射回波会因干涉效应,其信号幅度随频率变化而剧烈起伏。相比之下,来自平整底面的反射回波,其幅度对频率变化的依赖性要小得多。
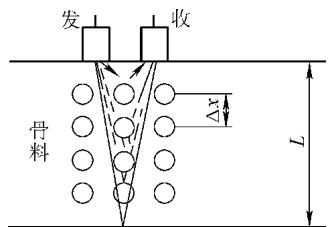
图4 混凝土路面结构层的理想化模型
利用这一特性,可以设计一套处理流程(如图5)。首先用时窗截取包含底面反射和散射信号的波段,接着让信号通过一组中心频率不同的带通滤波器(例如,从50kHz到175kHz,间隔25kHz,采用FIR数字滤波器设计)。对各滤波器的输出进行幅度归一化补偿,最后进行极小化处理。处理后的输出序列中(如图6),最高峰值的位置便清晰地指向了底面反射波。该方法的测量误差可以控制在3%至5%。
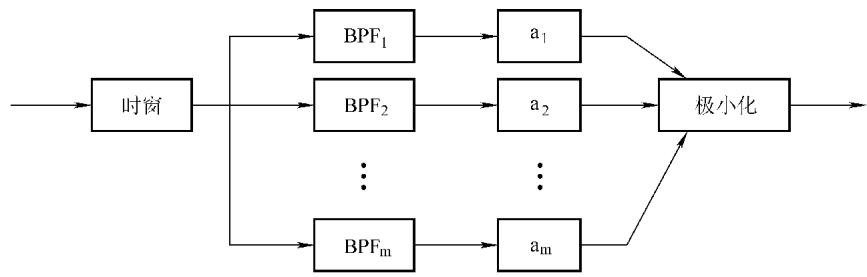
图5 分离谱法系统框图
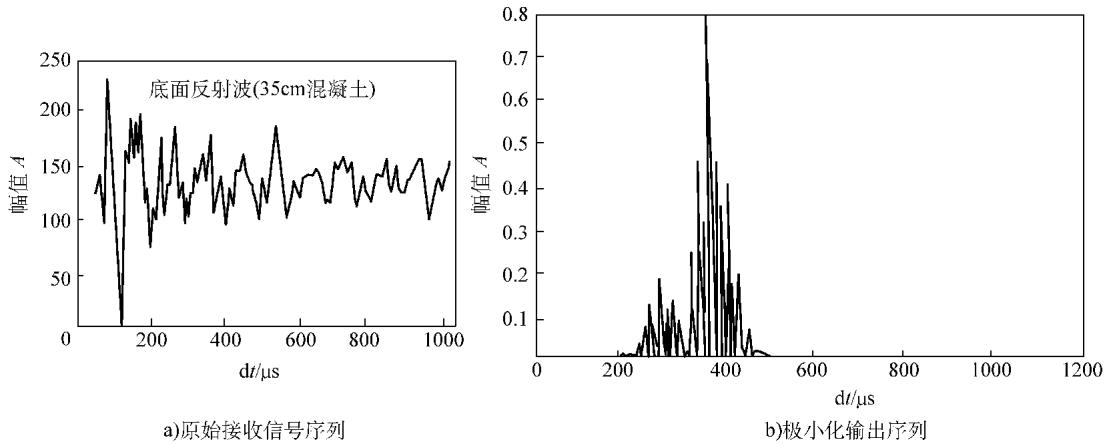
图6 原始接收信号(a)与极小化输出序列(b)对比
要获得信噪比高、结果可靠的图谱,对信号处理算法的选择、滤波器参数的配置都有极高要求。这正是专业检测实验室的核心价值所在。
精工博研测试技术(河南)有限公司(原郑州三磨所国家磨料磨具质量检验检测中心),央企,国字头检测机构,专业的权威第三方检测机构,专业检测混凝土无损检测,可靠准确。欢迎沟通交流,电话19939716636
除了几何尺寸,材料的力学性能,如动弹性模量(E<sub>d</sub>)和泊松比(ν),对评估结构承载能力和耐久性同样关键。这些参数与超声波在固体中的传播速度(纵波速度c<sub>p</sub>、横波速度c<sub>S</sub>、表面波速度c<sub>R</sub>)之间存在明确的物理关系:
c<sub>p</sub> = √[(E<sub>d</sub>/ρ) * (1 - ν) / ((1 + ν)(1 - 2ν))]
c<sub>S</sub> = √[(E<sub>d</sub>/ρ) * 1 / (2(1 + ν))]
c<sub>R</sub> = [(0.87 + 1.12ν) / (1 + ν)] * √[(E<sub>d</sub>/ρ) * 1 / (2(1 + ν))]
其中 ρ 是材料密度。通过这些基本关系式可以推导出,只要测得 c<sub>p</sub> 和 c<sub>S</sub>,或 c<sub>p</sub> 和 c<sub>R</sub>,就可以联立求解出动弹性模量 E<sub>d</sub> 和泊松比 ν。
在路面现场,通常采用平测法(如图7),同时测量纵波速度 c<sub>p</sub> 和表面波速度 c<sub>R</sub>。当纵波换能器置于路面时,接收到的波形中,最先到达的是纵波(图7中标记1),随后振幅突然增大的部分是表面波(初至点标记2,第一个峰值点标记3)。
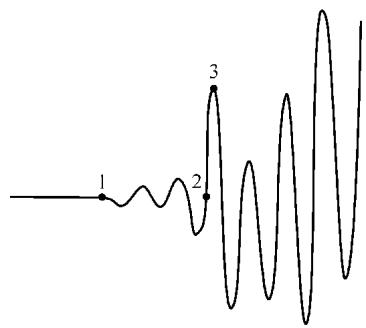
图7 平测法接收波形
为了消除仪器零读数和材料不均匀性的影响,实践中采用多点平测法。通过在不同距离上进行测量,绘制声时-距离曲线(如图8)。该图上会呈现出两条斜率不同的直线,其斜率的倒数分别对应纵波和表面波的速度。由此求得 c<sub>p</sub> 和 c<sub>R</sub> 后,即可计算出路面混凝土的动弹性模量和泊松比。
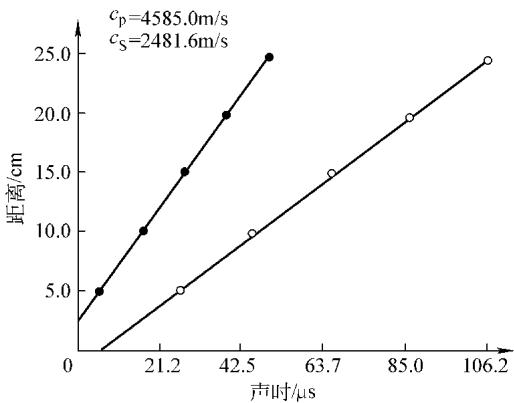
图8 声时-距离曲线
表1展示了在某高速公路上,利用超声波法测定的结果与传统取芯法的对比,同时给出了计算得到的动弹性模量和泊松比。
表1 高速公路水泥混凝土路面动弹性模量和泊松比的测量结果
| 桩号位置 | 超声波法-回弹值 | 超声波法-厚度/cm | 超声波法-抗折强度/MPa | 取芯法-厚度/cm | 取芯法-抗折强度/MPa | 动弹性模量/(10³MPa/m²) | 泊松比 |
|---|---|---|---|---|---|---|---|
| K298+223 | 38.8 | 23.9 | 5.62 | 23.8 | 5.87 | 44.4 | 0.26 |
| K300+865 | 39.5 | 22.9 | 5.88 | 22.7 | 6.07 | 44.8 | 0.27 |
| K301+500 | 42.0 | 22.5 | 5.45 | 22.8 | 5.13 | 49.5 | 0.25 |
| K303+915 | 34.9 | 25.4 | 4.90 | 25.5 | 4.73 | 46.1 | 0.26 |
| K304+601 | 40.4 | 25.9 | 6.40 | 26.0 | 6.54 | 46.5 | 0.26 |
| K305+030 | 42.6 | 24.4 | 5.20 | 23.8 | 5.09 | 48.1 | 0.25 |
| K306+190 | 48.4 | 22.7 | 5.65 | 22.9 | 6.13 | 47.1 | 0.24 |
| K309+850 | 46.6 | 22.7 | 6.15 | 22.0 | 6.38 | 45.5 | 0.24 |
| K310+345 | 44.1 | 22.6 | 5.82 | 23.6 | 5.57 | 48.4 | 0.24 |
| K312+850 | 46.3 | 27.5 | 6.50 | 28.9 | 6.78 | 48.1 | 0.25 |
抗折强度是路面混凝土工程质量的核心验收指标。传统方法依赖于制作标准试件进行破坏性试验,但试件的养护条件和密实度很难与实际路面完全一致,导致其代表性存疑。而现场取芯进行劈拉试验,又会破坏路面结构。
超声波-回弹综合法为现场无损评估抗折强度提供了新途径。该方法结合了超声波声速(反映材料内部致密性)和回弹值(反映表面硬度)两个参数,通过建立经验回归公式来预测抗折强度。
为建立可靠的回归模型,研究人员根据工程要求(如设计抗折强度4.5MPa,坍落度1-2.5cm)和常用配合比(如425/525水泥,石灰石/花岗岩碎石等),在室内制作了大量试件,并在不同龄期(7d, 28d)进行试验。通过对试验数据进行回归分析,可建立如下形式的抗折强度回归公式:
f<sub>cu</sub><sup>c</sup> = 1.4554 × 10<sup>-5</sup> * R<sup>0.434</sup> * c<sup>1.3239</sup>
其中:
f<sub>cu</sub><sup>c</sup>:混凝土抗折强度 (MPa)R:回弹值c:超声波声速 (m/s)该经验公式的相关系数为0.88,标准误差为7.5%,表明其具有良好的预测精度。从表1的数据对比中也可以看出,在高速公路现场,采用该综合法检测的抗折强度与取芯法的结果相当接近,验证了其在实际工程中应用的有效性和可靠性。


 首页
首页
 检测领域
检测领域
 服务项目
服务项目
 咨询报价
咨询报价