非线性超声波技术：深入洞察材料微观损伤的窗口

在无损检测领域，传统的线性超声波方法通过测量声速、衰减等参数来评估材料的宏观缺陷，其应用已相当成熟。然而，当损伤处于萌芽阶段，例如材料内部出现微裂纹、位错累积或性能发生早期退化时，线性声学参数的变化往往微乎其微，难以有效检出。那么，是否存在一种能够放大这些细微变化的检测手段？非线性超声波法正是为此而生。

它与常规线性超声波的根本区别在于，它利用了材料本身固有的非线性响应。当一束足够强的超声波（基波）在试件中传播时，它不再是完美的正弦波，而是会发生畸变。这种畸变意味着能量从基频 ω₀（振幅 A₀）向其高频谐波，如二次谐波 2ω₀（振幅 A₂）、三次谐波 3ω₀ 等转移。

这种谐波的产生，本质上是材料应力-应变关系偏离理想线性（胡克定律）的一种宏观体现。其微观根源在于晶格的非谐性振动、位错运动、以及晶界、界面等微观缺陷的存在。这些微观结构的变化，恰恰是材料在承受力学或环境作用下发生损伤的早期征兆。因此，通过精确捕捉谐波信号的强度，我们便能反向推断材料内部的微观损伤状态，实现对早期失效的灵敏预警。

量化非线性：β参数的物理意义与测量

为了定量描述材料的非线性程度，我们引入了非线性参数 β。这个参数构筑了从微观物理到宏观测量的桥梁。

从材料本构关系出发，β 可由二阶弹性模量 C_ij 和三阶弹性模量 C_klm 的组合来定义。例如，对于各向同性材料中的纵波，其关系式为：

β = 3 + (C₁₁₁ / C₁₁)

这个定义揭示了 β 直接关联于材料更高阶的弹性行为，而三阶弹性常数对微观结构的变化极为敏感。

从实验测量的角度，β 参数也可以通过基波和二次谐波的位移振幅 A₁ 和 A₂ 来表达，这为实际检测提供了可操作的路径：

β = 8A₂ / (K²zA₁²)

式中，A₁ 和 A₂ 分别是基波和二次谐波的振幅；z 是超声波的传播距离（通常为试样厚度）；K 是超声纵波的波矢，由基频 ω₀ 和纵波相速度 C_l 决定 (K = ω₀ / C_l)。这个公式的价值在于，它将一个抽象的材料非线性度，转化为了几个可以被精确测量的物理量之间的关系。

高精度测量方案：激光干涉法

要准确捕获由非线性效应产生的微弱谐波信号，对测量技术提出了极高要求。激光干涉仪为此提供了一种理想的解决方案，其原理如图1所示。

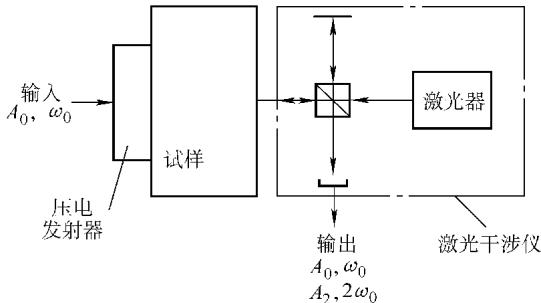
图1 用激光干涉仪进行非线性超声波试验的原理图

激光干涉仪发出的光束被分为两路：一束作为测量光射向试样表面并反射，另一束作为参考光从参考镜反射。当超声波到达试样表面引起瞬态位移时，测量光束的光程会发生微小改变，导致其与参考光束重新组合后的干涉信号强度发生相应变化。

相较于传统的压电或电容换能器，激光干涉法具备显著优势：

• 非接触式测量：避免了接触式探头带来的耦合剂影响和负载效应。
• 高空间分辨率：通过聚焦透镜，激光光斑直径可达微米量级（典型值为20μm），只需极小的平整区域即可进行测量，并能实现对声场的逐点扫描。
• 信号关系简单：当表面位移远小于激光波长时，所测得的光信号强度与真实位移之间存在简单的线性关系，便于信号解调和准确定量。

应用实例：淬火钢微观结构变化的灵敏表征

非线性超声测量的威力在材料性能评估中已得到证实，例如用于检测高温合金的脆化、铝板胶接质量等。下面我们通过一个淬火马氏体钢的案例，来直观感受其对微观结构变化的敏感性。

实验研究了不同碳含量的淬火钢试样，其非线性参数 β 和传统纵波速度 C_l 的变化如表1所示。

表1 在淬火状态马氏体钢试样中，碳含量对非线性超声波参数 β 和纵波速度 C_l 的影响

注：C_l0 和 β₀ 为9310钢的参考值。

从数据中可以清晰地看到，随着碳含量从0.1%增加到0.40%，纵波速度 C_l 的相对变化仅为0.6%，几乎不敏感。然而，非线性参数 β 的相对值却增大了11%。

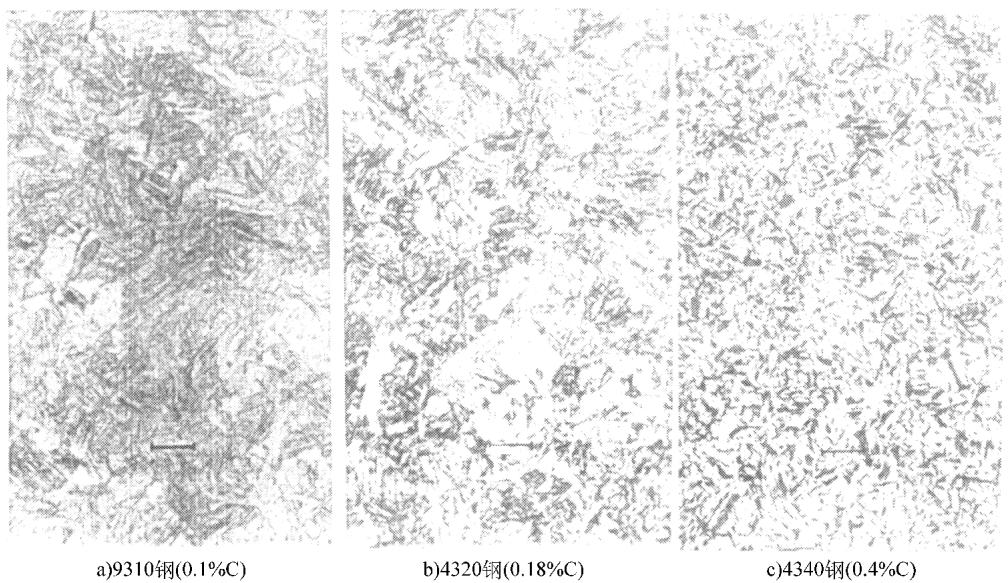
图2 淬火状态钢试样的光学显微照片（放大1000×，图中水平黑线相当于10μm）

结合X射线衍射分析，这种差异得到了解释：碳含量的增加导致淬火后马氏体中的位错密度（N）显著增高（从1.5×10¹¹/cm²增至3.6×10¹¹/cm²），从而引起了更大的内应力。这清晰地表明，非线性参数β能够捕捉到传统声速测量所忽略的、由位错和内应力引发的微观结构演化。

要获得可靠的非线性声学参数，对实验系统的搭建、信号的激发与接收、以及数据的解译都有着极高的专业要求。这正是专业检测实验室的核心价值所在。 精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测材料非线性声学参数，可靠准确。欢迎沟通交流，电话19939716636

附录：常用弹性常数换算表

为便于工程计算和理论分析，下表列出了各向同性材料常用弹性常数之间的换算关系。

表2 弹性常数换算表