在辐射物理与探测技术领域,理解射线如何与物质发生相互作用是所有应用的基础。无论是进行无损检测、材料分析,还是设计辐射屏蔽,其核心都离不开对粒子或光子穿行于介质中能量损失、方向偏转等一系列物理过程的精确把握。本文将深入探讨两种常见的射线——β射线(高速电子流)和γ射线(高能光子流)——与物质相互作用的核心机理、关键差异及其在实践中的意义。
在同位素应用中,我们通常遇到的β射线是能量上限约2 MeV的高速电子。由于携带电荷且质量轻,β粒子穿行在物质中时,其路径并非一条直线,而是经历一系列复杂的相互作用,最终能量耗尽而被吸收。这个过程主要涉及能量损失和散射两大机制。
β粒子在物质中“减速”主要通过两种方式:电离损失和辐射损失。这两种机制的相对重要性取决于β粒子的能量和吸收物质的原子序数。
电离损失 (Ionization Loss) 这可以看作是β粒子与物质原子核外电子的非弹性碰撞。在碰撞中,β粒子将一部分能量转移给原子电子,导致后者被激发或直接被“撞”出原子,形成电离。这个过程是β粒子在低能量段最主要的能量损失方式。有趣的是,在特定吸收物质中,产生一个电子-离子对所需的平均电离能是一个基本恒定的值,与入射β粒子的能量无关。例如,在空气中,这个值大约是30 eV。
辐射损失 (Radiative Loss) 当高速运动的β粒子掠过原子核附近时,会受到原子核强大的库仑场作用而发生偏转,即产生加速度。根据经典电磁理论,带电粒子加速运动会辐射电磁波,这种现象被称为韧致辐射(Bremsstrahlung,德语意为“刹车辐射”)。韧致辐射产生的光子能量谱是连续的,从零一直延伸到β粒子的最大能量。与电离损失不同,辐射损失的效率与两个因素密切相关:它与吸收物质原子序数(Z)的平方成正比,也与β粒子自身的能量成正比。这意味着,对于重元素(如铅)和高能β粒子,辐射损失会变得尤为重要。
下图直观地展示了电子在不同物质中,这两种能量损失机制的相对关系。
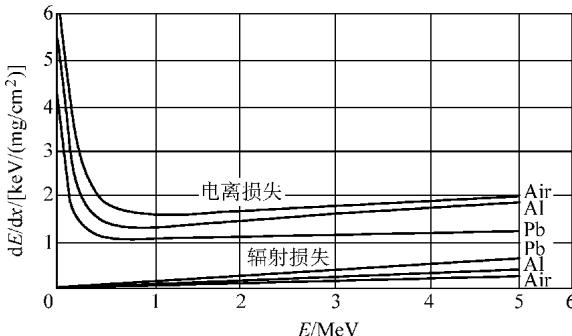 图1 电子的辐射损失和电离损失
图1 电子的辐射损失和电离损失
除了能量损失,β粒子还会与原子核库仑场发生弹性散射。在此过程中,粒子只改变运动方向,几乎不损失能量。由于β粒子质量极小,单次散射的角度可能非常大,且在被完全吸收前会经历多次散射。散射的剧烈程度同样与物质的原子序数(Z)和粒子能量有关:Z越大,粒子能量越低,散射效应就越强烈。在某些低能β射线与高Z材料的相互作用中,散射系数甚至可达百分之几十,这是在实际应用中绝不能忽视的因素。
综合了电离、激发、辐射和多次散射等一系列过程后,β粒子最终耗尽能量被物质吸收。它在物质中走过的总路程被称为射程 (Range)。但由于其路径是曲折的,射程这个概念并不像宏观物体那样严格。同时,来自同位素源的β射线能量本身就呈连续谱分布,因此我们通常用其最大能量(Emax)对应的最大射程来表征其穿透能力。
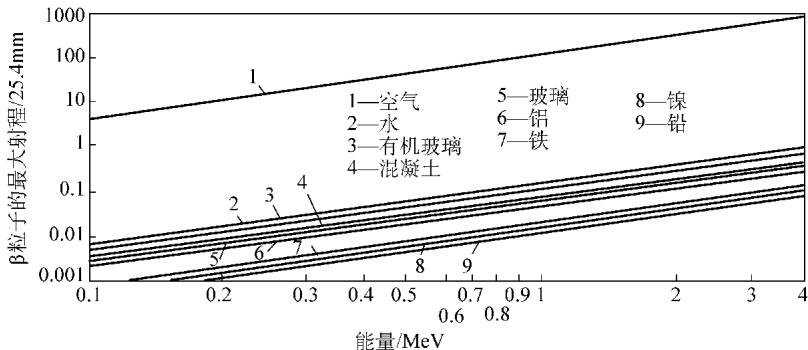 图2 几种物质中β粒子最大射程与能量的关系
图2 几种物质中β粒子最大射程与能量的关系
当吸收物质的厚度远小于β射线的射程时,其强度衰减近似遵循指数规律:
I = I₀ * e<sup>-μ<sub>m</sub>ρx</sup> = I₀ * e<sup>-μ<sub>m</sub>x<sub>m</sub></sup> (1)
此公式中:
I₀ 和 I 分别是穿透物质前后的β粒子强度。ρ 是物质的密度,x 是物质的厚度。μ<sub>m</sub> 是质量吸收系数 (μ<sub>m</sub> = μ/ρ),它描述了单位质量厚度的物质对射线的吸收能力。x<sub>m</sub> 是质量厚度 (x<sub>m</sub> = ρx),这是一个非常有用的参数,因为它在一定程度上消除了材料密度的影响。实验表明,质量吸收系数μ<sub>m</sub>与吸收体的原子序数Z和相对原子质量A的比值(Z/A)成正比,并随Z的增加而缓慢增加。它与β射线最大能量E<sub>max</sub>的关系可通过以下经验公式估算:
μ<sub>m</sub> = 22 / E<sub>max</sub><sup>1.33</sup> (2)
其中 μ<sub>m</sub> 的单位是 cm²/g,E<sub>max</sub> 的单位是 MeV。
表1给出了不同能量的β射线在铝中的吸收系数值。
表1 不同能量β射线在铝中的线吸收系数μ和质量吸收系数μm
| Emax /MeV | μm /(cm²/g) | μ /cm⁻¹ | Emax /MeV | μm /(cm²/g) | μ /cm⁻¹ |
|---|---|---|---|---|---|
| 0.15 | 256 | 692 | 1.2 | 9.9 | 26.7 |
| 0.20 | 182 | 492 | 1.4 | 7.9 | 21.3 |
| 0.30 | 98 | 264 | 1.6 | 6.5 | 17.5 |
| 0.40 | 59 | 159 | 1.8 | 5.7 | 15.4 |
| 0.50 | 39 | 105 | 2.0 | 4.9 | 13.2 |
| 0.60 | 29 | 78.5 | 2.2 | 4.6 | 12.4 |
| 0.70 | 23 | 62.1 | 2.4 | 4.1 | 11.1 |
| 0.80 | 18.6 | 50.2 | 2.6 | 3.8 | 10.2 |
| 0.90 | 15.3 | 41.3 | 2.8 | 3.6 | 9.7 |
| 1.00 | 13.0 | 35.1 | 3.0 | 3.3 | 8.9 |
另一个实用概念是半吸收厚度 (Δ1/2),即能将β射线强度减弱一半所需的质量厚度。
Δ<sub>1/2</sub> = ln(2) / μ<sub>m</sub> = 0.693 / μ<sub>m</sub> (3)
同样,它也有一个与最大能量相关的经验公式:
Δ<sub>1/2</sub> = 0.032 * E<sub>max</sub><sup>1.33</sup> (4)
表2 不同能量β射线在Al中的半吸收厚度 Δ1/2
| Emax /MeV | Δ1/2 /(mg/cm²) | Emax /MeV | Δ1/2 /(mg/cm²) | Emax /MeV | Δ1/2 /(mg/cm²) | Emax /MeV | Δ1/2 /(mg/cm²) |
|---|---|---|---|---|---|---|---|
| 0.15 | 2.7 | 0.60 | 24 | 1.2 | 70 | 2.2 | 150 |
| 0.20 | 3.8 | 0.70 | 30 | 1.4 | 87 | 2.4 | 168 |
| 0.30 | 7.0 | 0.80 | 37 | 1.6 | 107 | 2.6 | 180 |
| 0.40 | 11.7 | 0.90 | 45 | 1.8 | 121 | 2.8 | 195 |
| 0.50 | 17.5 | 1.00 | 53 | 2.0 | 140 | 3.0 |
γ射线与X射线本质上都是电磁辐射,只是产生机制不同。它们与物质的相互作用方式和β射线有着本质区别。γ射线不带电,穿透力更强,其相互作用是概率性的。在能量低于30 MeV的范围内,主要通过以下三种效应将其能量转移给物质:
当一个γ光子与物质原子作用时,它会把全部能量交给某个束缚态的轨道电子,光子自身则完全消失。获得能量的电子(称为光电子)脱离原子。光电子的动能 Eₑ 为:
Eₑ = hν - Eᵢ (5)
其中 hν 是入射γ光子的能量,Eᵢ 是该轨道电子的结合能。
光电效应的发生概率(截面)对能量和物质类型极为敏感:它近似与吸收体原子序数Z的四次方成正比,与γ光子能量的三次方成反比。这意味着,光电效应在低能区和高Z材料中占据绝对主导地位。
康普顿效应是γ光子与原子核外(通常是较外层)电子发生的非弹性散射。在此过程中,光子只将一部分能量转移给电子,使其成为反冲电子,而散射后的光子则以更低的能量和新的方向继续前进。这与光电效应的“全盘吸收”截然不同。反冲电子的能量 Eₑ 与散射角 θ(散射光子与入射光子方向的夹角)有关:
Eₑ = (hν)²(1 - cosθ) / [m₀c² + hν(1 - cosθ)] (6)
当散射角 θ = 180° 时,反冲电子获得最大能量:
Eₑₘₐₓ = hν / [1 + m₀c² / (2hν)] (7)
康普顿效应的截面近似与吸收体的原子序数Z成正比,且在很宽的中等能量范围内(约0.5 MeV至5 MeV)对能量变化不敏感,是中能区最主要的相互作用方式。
当γ光子的能量足够高(必须大于一个正负电子对的静止质量之和,即 2m₀c² ≈ 1.022 MeV)时,它在原子核的库仑场附近可能直接转化为一个电子和一个正电子。这个过程被称为电子对效应。入射光子的能量减去产生电子对所需的能量(1.022 MeV)后,剩余的能量转化为正负电子对的动能。
电子对效应的截面大致与吸收体原子序数Z的平方成正比,并随入射光子能量的增加而线性增加。因此,它在高能区(> 10 MeV)和高Z材料中成为主导。
由于γ射线的相互作用是概率性的,那些未与物质发生作用的光子会保持原有能量和方向穿过吸收层。因此,γ射线没有确定的“射程”,只有强度的衰减 (Attenuation)。其强度变化同样遵循指数衰减规律:
I = I₀ * e<sup>-μx</sup> = I₀ * e<sup>-μ<sub>m</sub>x<sub>m</sub></sup> (8)
这里的吸收系数 μ 或 μ<sub>m</sub> 的物理意义与β射线的不同,它代表的是光子发生上述三种相互作用的总概率。总吸收系数是三种效应吸收系数的总和:
μ = μ<sub>ph</sub> + μ<sub>c</sub> + μ<sub>p</sub> (9)
其中,μ<sub>ph}、μ<sub>c</sub> 和 μ<sub>p</sub> 分别代表光电效应、康普顿效应和电子对效应的吸收系数。
下图清晰地展示了在不同能量下,三种效应对总吸收系数的贡献。
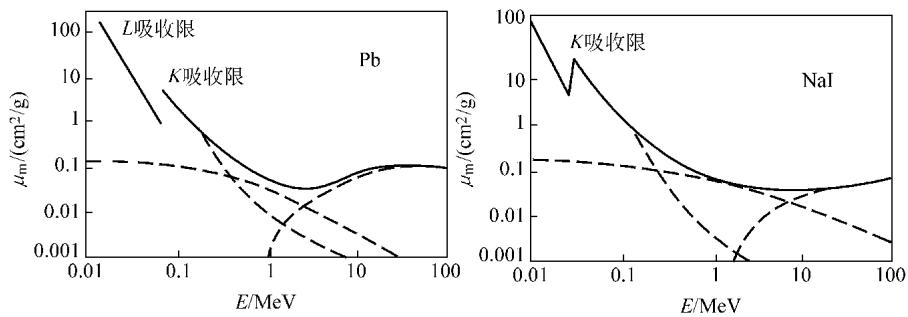 图3 某些材料的吸收系数与γ射线能量的关系
图3 某些材料的吸收系数与γ射线能量的关系
从图中可以看出,要精确评估材料对特定能量γ射线的屏蔽或吸收效果,必须准确掌握其在该能量下的质量衰减系数。这不仅需要理论计算,更依赖于高精度的实验测量。因此,要获得一张信噪比高、结果可靠的图谱,对样品制备、设备参数配置都有极高要求。这正是专业检测实验室的核心价值所在。
精工博研测试技术(河南)有限公司(原郑州三磨所国家磨料磨具质量检验检测中心),央企,国字头检测机构,专业的权威第三方检测机构,专业检测材料γ射线衰减系数测定,可靠准确。欢迎沟通交流,电话19939716636
同样,γ射线的半吸收厚度 (Δ1/2) 指的是能将其强度减弱一半的质量厚度:
Δ<sub>1/2</sub> = ln(2) / μ<sub>m</sub> = 0.693 / μ<sub>m</sub> (10)
以下表格提供了部分常见单质和材料对不同能量γ射线的质量衰减系数,这些数据是进行辐射防护设计和剂量学计算的重要依据。
表3 部分单质对不同能量γ射线的质量衰减系数 (单位: cm²/g)
| 光子能量 Eγ/MeV | Al (铝) | Si (硅) | Ti (钛) | Fe (铁) | W (钨) | Pb (铅) |
|---|---|---|---|---|---|---|
| 0.01 | 26.3 | 33.2 | 110.0 | 170.0 | 4.7 | 128.0 |
| 0.015 | 7.79 | 10.1 | 35.6 | 56.8 | 137.0 | 108.0 |
| 0.02 | 3.39 | 4.37 | 15.7 | 25.6 | 64.3 | 85.2 |
| 0.03 | 1.11 | 1.41 | 4.90 | 8.09 | 22.4 | 29.9 |
| 0.04 | 0.562 | 0.690 | 2.20 | 3.59 | 10.5 | 14.2 |
| 0.05 | 0.366 | 0.435 | 1.20 | 1.93 | 5.90 | 7.88 |
| 0.06 | 0.277 | 0.319 | 0.760 | 1.20 | 3.67 | 4.94 |
| 0.08 | 0.202 | 0.223 | 0.402 | 0.592 | 7.80 | 3.37 |
| 0.10 | 0.170 | 0.183 | 0.270 | 0.368 | 4.39 | 5.52 |
| 0.15 | 0.138 | 0.144 | 0.163 | 0.194 | 1.58 | 2.01 |
| 0.20 | 0.122 | 0.127 | 0.131 | 0.144 | 0.780 | 0.994 |
| 0.30 | 0.104 | 0.108 | 0.104 | 0.110 | 0.320 | 0.398 |
| 0.40 | 0.0926 | 0.0961 | 0.0905 | 0.0936 | 0.190 | 0.229 |
| 0.50 | 0.0844 | 0.0875 | 0.0817 | 0.0839 | 0.136 | 0.159 |
| 0.60 | 0.0779 | 0.0808 | 0.0750 | 0.0768 | 0.108 | 0.123 |
| 0.80 | 0.0683 | 0.0705 | 0.0656 | 0.0668 | 0.0799 | 0.0875 |
| 1.00 | 0.0614 | 0.0635 | 0.0588 | 0.0598 | 0.0655 | 0.0703 |
| 1.50 | 0.0500 | 0.0517 | 0.0479 | 0.0487 | 0.0498 | 0.0517 |
| 2.00 | 0.0431 | 0.0448 | 0.0417 | 0.0425 | 0.0436 | 0.0453 |
| 3.0 | 0.0355 | 0.0367 | 0.0351 | 0.0361 | 0.0403 | 0.0416 |
| 4.00 | 0.0310 | 0.0324 | 0.0318 | 0.0331 | 0.0400 | 0.0416 |
| 5.00 | 0.0283 | 0.0296 | 0.0299 | 0.0315 | 0.0406 | 0.0424 |
| 6.00 | 0.0266 | 0.0279 | 0.0288 | 0.0305 | 0.0416 | 0.0436 |
| 8.00 | 0.0243 | 0.0257 | 0.0275 | 0.0298 | 0.0439 | 0.0459 |
| 10.00 | 0.0232 | 0.0244 | 0.0273 | 0.0298 | 0.0465 | 0.0485 |
表4 部分材料对不同能量γ射线的质量衰减系数 (单位: cm²/g)
| 光子能量 Eγ/MeV | 空气 | 二氧化硅 | 水 | 聚苯乙烯 | 有机玻璃 | 混凝土 |
|---|---|---|---|---|---|---|
| 0.01 | 4.99 | 19.0 | 5.18 | 2.13 | 3.25 | 26.9 |
| 0.015 | 1.55 | 5.73 | 1.58 | 0.755 | 1.06 | 8.24 |
| 0.02 | 0.752 | 2.49 | 0.775 | 0.424 | 0.551 | 3.59 |
| 0.03 | 0.349 | 0.859 | 0.370 | 0.259 | 0.298 | 1.19 |
| 0.04 | 0.248 | 0.463 | 0.267 | 0.217 | 0.234 | 0.605 |
| 0.05 | 0.208 | 0.318 | 0.227 | 0.199 | 0.208 | 0.392 |
| 0.06 | 0.188 | 0.252 | 0.206 | 0.188 | 0.193 | 0.295 |
| 0.08 | 0.167 | 0.194 | 0.184 | 0.173 | 0.176 | 0.213 |
| 0.10 | 0.154 | 0.169 | 0.171 | 0.163 | 0.164 | 0.179 |
| 0.15 | 0.136 | 0.140 | 0.151 | 0.145 | 0.146 | 0.144 |
| 0.20 | 0.123 | 0.126 | 0.137 | 0.132 | 0.133 | 0.127 |
| 0.30 | 0.107 | 0.108 | 0.119 | 0.115 | 0.115 | 0.108 |
| 0.40 | 0.0954 | 0.0959 | 0.106 | 0.103 | 0.103 | 0.0963 |
| 0.50 | 0.0870 | 0.0874 | 0.0968 | 0.0938 | 0.0941 | 0.0877 |
| 0.60 | 0.0805 | 0.0808 | 0.0896 | 0.0868 | 0.0871 | 0.0810 |
| 0.80 | 0.0707 | 0.0707 | 0.0786 | 0.0763 | 0.0765 | 0.0709 |
| 1.00 | 0.0636 | 0.0636 | 0.0707 | 0.0685 | 0.0678 | 0.0637 |
| 1.50 | 0.0518 | 0.0518 | 0.0575 | 0.0558 | 0.0559 | 0.0519 |
| 2.00 | 0.0445 | 0.0447 | 0.0494 | 0.0478 | 0.0480 | 0.0448 |
| 3.00 | 0.0358 | 0.0366 | 0.0397 | 0.0383 | 0.0385 | 0.0365 |
| 4.00 | 0.0308 | 0.0317 | 0.0340 | 0.0327 | 0.0329 | 0.0319 |
| 5.00 | 0.0275 | 0.0287 | 0.0308 | 0.0290 | 0.0292 | 0.0290 |
| 6.00 | 0.0252 | 0.0266 | 0.0277 | 0.0263 | 0.0266 | 0.0270 |
| 8.00 | 0.0223 | 0.0241 | 0.0243 | 0.0228 | 0.0232 | 0.0245 |


 首页
首页
 检测领域
检测领域
 服务项目
服务项目
 咨询报价
咨询报价