疲劳裂纹扩展速率 (da/dN) 的原理与试验方法解析

日期：2025-07-23 浏览：9

疲劳裂纹扩展速率 (da/dN) 的原理与试验方法解析

在材料科学与工程领域，尤其是在结构完整性评估和寿命预测中，精确理解疲劳裂纹的扩展行为至关重要。构件在循环载荷作用下，其内部的微小缺陷会逐渐演变为宏观裂纹，并以一定的速率向前扩展，直至最终导致结构失效。这一过程的核心驱动力，源于裂纹尖端区域循环塑性应变的累积。

自上世纪60年代Paris等人开创性地使用断裂力学方法来表征疲劳裂纹扩展以来，学术界和工业界已经发展出一套成熟的理论与测试体系。其核心思想在于，将裂纹扩展速率 da/dN（每次载荷循环下裂纹的扩展长度）与应力强度因子范围 ΔK 建立关联。

ΔK 定义为在一个载荷循环中，应力强度因子 K 的最大值 K_max 与最小值 K_min 之差，通常只考虑其正值部分：

$$ /begin{array}{rl} & {/Delta K = K_{/mathrm{max}} - K_{/mathrm{min}} = (1 - /mathrm{R})K_{/mathrm{max}}/quad /mathrm{for}/quad /mathrm{R}/geq 0}// & {/Delta K = K_{/mathrm{max}}/quad /mathrm{for}/quad /mathrm{R}/leq 0} /end{array} $$

其中，R 为应力比 (R = σ_min/ σ_max = K_min/ K_max)。

金属材料典型的疲劳裂纹扩展行为，在 da/dN vs. ΔK 的双对数坐标系下，呈现出一条标志性的“S”形曲线，如下图所示。

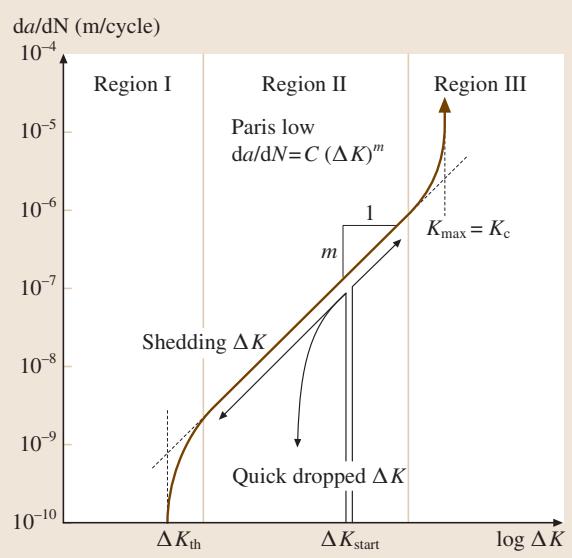
图1. 应力强度因子范围 ΔK 与裂纹扩展速率 da/dN 的关系示意图

这条曲线清晰地揭示了裂纹扩展的三个阶段：

区域 I：门槛区 (Threshold Region)。当 ΔK 低于一个临界值，即疲劳裂纹扩展门槛值 ΔK_th 时，裂纹扩展速率极其缓慢，甚至在工程上可以认为裂纹停止扩展。ΔK_th 是材料抵抗疲劳裂纹萌生的一个关键下限指标。
区域 II：稳定扩展区 (Stable Growth Region)。在中间的 ΔK 值范围内，log(da/dN) 与 log(ΔK) 呈现出近似线性的关系。这个区域的扩展行为主要由 ΔK 控制，对应力比 R 的敏感度较低。这一关系可用经典的Paris公式来描述：

$$ /mathrm{da} / /mathrm{d}N = C(/Delta K)^{m} $$

此即大名鼎鼎的Paris定律。其中，C 和 m 是通过实验确定的材料常数，它们共同构成了材料在疲劳载荷下的“性能指纹”。
区域 III：失稳扩展区 (Unstable Growth Region)。当 ΔK 进一步增大，裂纹扩展会急剧加速。即便外部施加的应力幅 Δσ 保持不变，裂纹的快速延伸也会导致 ΔK 迅速攀升，形成正反馈。最终，当循环中的最大应力强度因子 K_max (= ΔK / (1 - R)) 达到材料的断裂韧性 K_c 时，裂纹将转入失稳断裂，此时 da/dN 趋于无穷大。

基于 ASTM E647 标准的测试方法学

为了确保测试数据的可靠性与可比性，美国材料与试验协会（ASTM）自1978年起便发布了基于断裂力学的疲劳裂纹扩展速率测量标准，即 ASTM E 647。以下是对该标准核心内容的提炼与解读。

1. 标准试样

标准规定了两种主要试样类型：紧凑拉伸试样（Compact Tension, C(T)）和中心裂纹拉伸试样（Middle Tension, M(T)）。

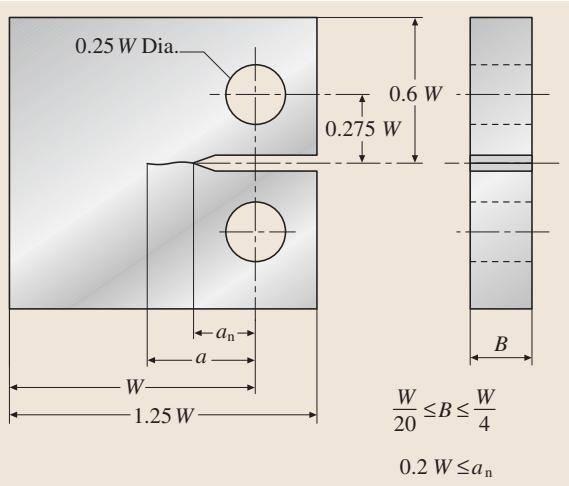
图2. 紧凑拉伸C(T)试样

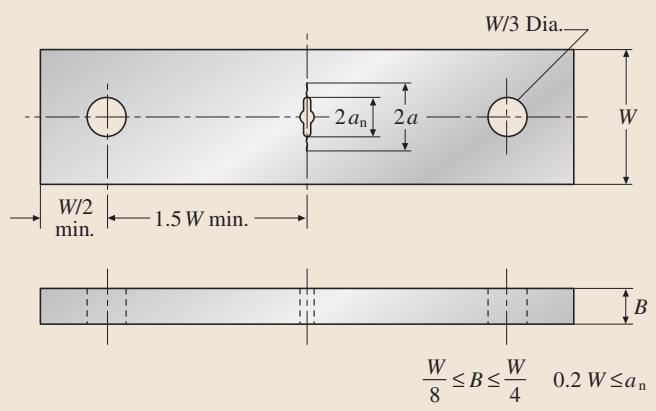
图3. 中心裂纹M(T)试样

C(T)试样：推荐用于拉-拉加载模式。其构型与断裂韧性测试中的C(T)试样基本一致，但对厚度 B 的要求有所放宽。
M(T)试样：可用于拉-拉或拉-压加载。

一个重要的区别在于，疲劳裂纹扩展速率测试不强制要求满足平面应变状态。因此，试样厚度可以更灵活地选择。实际上，较薄的试样有时反而更优，因为它可以避免产生不规则的“拇指状”裂纹前缘，从而降低裂纹长度测量的误差。

2. 预制疲劳裂纹

测试的起点并非机械加工的尖锐缺口，而是在此基础上通过疲劳加载引入一条“自然”的、锋利的初始裂纹，即预制疲劳裂纹。这一步至关重要，其目的是消除加工缺口对后续 K 值标定和裂纹扩展行为的干扰。

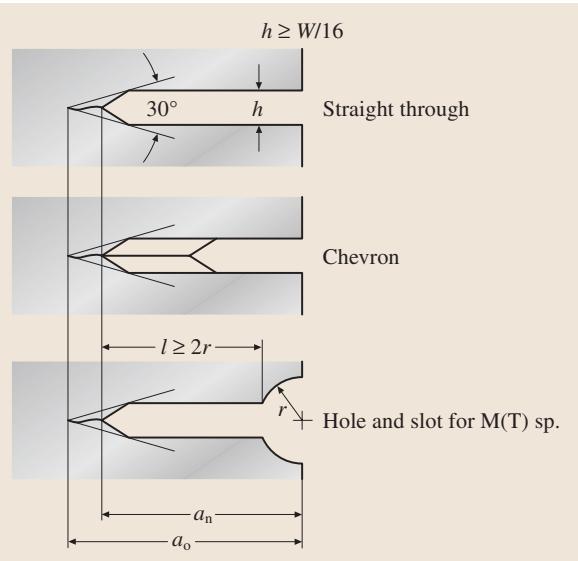
图4. 从机加工缺口预制疲劳裂纹的示例。(a) ΔK递增测试, (b) ΔK递减测试

标准对此有严格规定：

几何形状：加工缺口的轮廓必须位于以疲劳预裂纹尖端为顶点、夹角为30°的线内。
长度：预裂纹长度不应小于 0.1B、h 或 1mm 中的最大值。
加载水平：预制裂纹过程中的 K_max 必须低于后续正式测试的初始 K_max。特别是在测量门槛值 ΔK_th 附近的数据时，建议预裂纹的扩展速率低于 10^-8 m/cycle。
平直度：在试样前后表面测量的预裂纹尺寸差异不得超过 0.25B。

3. 裂纹扩展的监测与加载程序

在受控的载荷幅值下，需要精确测量裂纹长度随加载循环次数的变化（即 a-N 曲线）。常用方法包括：

目测法：使用移动显微镜直接观测。
柔度法：通过监测特定载荷下的裂纹开口位移变化来反推裂纹长度。
电位法：利用裂纹扩展导致试样电势差变化的原理进行测量。

标准推荐将目测法与柔度法或电位法之一结合使用，以确保精度。所有方法的最小分辨率要求优于 0.1mm 或 0.002W（W为试样宽度）中的较大者。

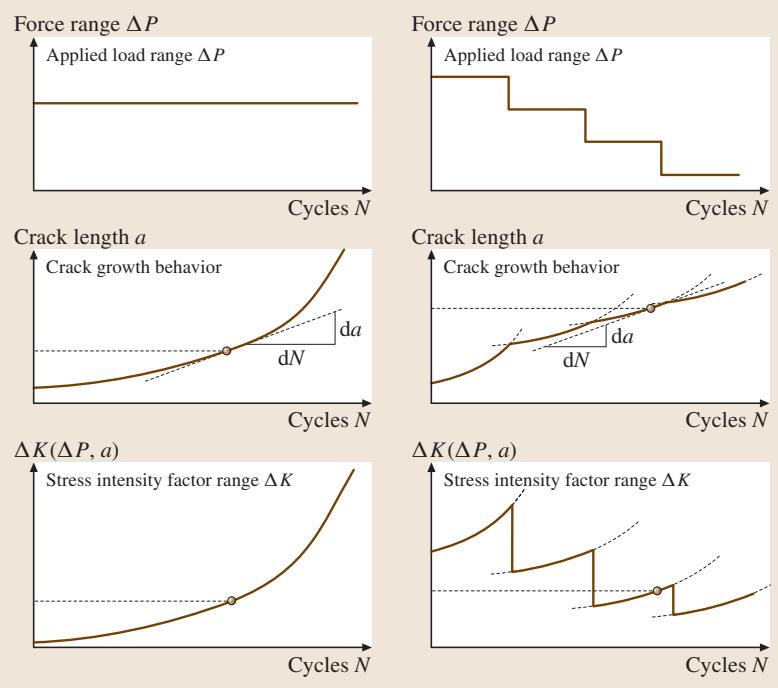
图5. 施加载荷与裂纹扩展及应力强度因子范围的对应关系

根据目标测量的 da/dN 范围，可以选择两种加载程序：

ΔK 递增法：保持载荷范围 ΔP 不变。随着裂纹 a 的增长，ΔK 会自然增加。此法适用于测量高于 10^-8 m/cycle 的速率，操作相对简单。
ΔK 递减法：用于测量低于 10^-8 m/cycle 的低速率区，尤其是门槛值 ΔK_th。测试从较高的 ΔK 开始，随着裂纹的扩展，逐步减小载荷 ΔP（即“载荷卸减”）。载荷的卸减必须足够平缓，以避免载荷历史效应对结果产生干扰。通常，每一步的载荷减小量不超过前一步最大载荷 P_max 的10%，且每一步减载后，裂纹需至少扩展0.5mm。

不恰当的载荷卸减可能导致测得的 da/dN-ΔK 曲线偏离材料的真实属性，这主要是由于前序较高载荷在裂纹尖端留下的塑性区产生了应变硬化和残余压应力，从而人为地提高了材料的抗疲劳扩展能力，导致结果偏于保守。获取准确可靠的低速率区数据，对实验操作提出了极高的要求。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测材料疲劳裂纹扩展速率，可靠准确。欢迎沟通交流，电话19939716636

4. 数据处理与分析

从实验得到的 a-N 数据，需要通过数值方法计算出 da/dN。标准推荐了两种方法：

割线法 (Secant Method)：计算 a-N 曲线上相邻两个数据点之间的直线斜率。 $$ (/mathrm{da} / /mathrm{d}N){/tilde{a}} = (a{i + 1} - a_i) / (N_{i + 1} - N_i) $$ 计算得到的速率是 a_i 到 a_i+1 区间内的平均速率，因此对应的 ΔK 值应使用该区间的平均裂纹长度 ã = (a_i+1 + a_i)/2 来计算。此法简单直接，但容易引入数据散射。
增量多项式法 (Incremental Polynomial Method)：对一组连续的数据点（通常为3到9个）进行二阶多项式拟合。 $$ /hat{a}i = b_0 + b_1(N_i - C_1) / C_2 + b_2/Big[(N_i - C_1) / C_2^2/Big] $$ 然后通过对拟合的多项式求导来计算在中心点 N_i 处的瞬时裂纹扩展速率。 $$ (/mathrm{da} / /mathrm{d}N){/hat{a} i} = b_1 / C_2 + 2b_2(N_i - C_1) / C_2^2 $$ 此方法通过数值平滑，通常能得到离散度更小的数据。

5. 数据有效性与应用考量

所有数据点都必须满足线弹性断裂力学（LEFM）的适用条件。标准给出了相对宽松的试样尺寸要求，以确保试样在测试过程中整体上处于弹性状态。

最终得到的 da/dN-ΔK 关系和 ΔK_th 值，是进行结构损伤容限设计和寿命预测的基石。通过对Paris公式进行积分，可以预测已知初始缺陷尺寸的构件在服役载荷下扩展至临界尺寸所需的循环次数。

然而，在应用这些数据时，还必须审慎考虑两个复杂但至关重要的因素：

裂纹闭合效应 (Crack Closure Effect)：在拉-拉循环加载中，即使名义载荷为拉应力，裂纹尖端后方的区域也可能因为塑性变形、断口粗糙度或腐蚀产物等原因而提前接触，产生残余压应力。这种“闭合”现象会屏蔽掉一部分外加载荷，使得驱动裂纹扩展的有效应力强度因子范围 ΔK_eff 小于名义上的 ΔK。忽略此效应会高估材料的 ΔK_th，导致不安全的设计。
小裂纹效应 (Small Crack Effect)：当结构中的初始裂纹尺寸与材料微观组织尺度相当时（通常小于0.5-1.0mm），其扩展行为可能与基于标准试样（长裂纹）测得的规律显著不同。小裂纹的扩展速率通常比相同 ΔK 下的长裂纹更快，甚至可以在低于 ΔK_th 的条件下扩展。这可能源于微观组织的不连续性以及断裂力学连续介质假设的局限性。