断裂力学基本原理

断裂力学的核心思想在于，它承认材料中必然存在裂纹或类似缺陷，并以此为出发点，研究含裂纹构件的强度和寿命。其基本准则可以概括为：一个尖锐裂纹尖端前方的应力应变场，能够通过一个单一参量来表征。这个参量，例如应力强度因子 K，是外加应力、裂纹尺寸和几何边界条件的函数。

预制裂纹的扩展或断裂起始，必然受控于裂纹尖端区域的应力或应变状态。这意味着，我们可以用一个断裂力学参量来描述裂纹体的断裂行为。这与传统材料力学中，用等效应力 σ_eq 是否达到材料屈服强度 σ_ys 来判断塑性屈服的行为，有异曲同工之妙。裂纹尖端应力/应变场的相似性准则预示着，在相同的环境条件下，相似的力学状态会导致同一种断裂模式。一旦我们通过实验室测试，用断裂力学参量描述了材料的抗断裂能力（即断裂韧性），我们就可以在不深入探讨具体断裂机理的情况下，推断该材料在不同外加应力、裂纹尺寸和几何构型下的断裂行为。如图1所示，断裂力学方法为强度评估引入了三个关键变量。

断裂力学可分为两大分支：线弹性断裂力学 (Linear Elastic Fracture Mechanics, LEFM) 和弹塑性断裂力学 (Elastic-Plastic Fracture Mechanics, EPFM)。

对于断裂韧性较低的材料，其断裂通常发生在裂纹尖端小范围的塑性屈服条件下，这类问题可以通过线弹性断裂力学进行分析。LEFM的核心是基于弹性应力分析的应力强度因子 K。而对于金属材料，它们在裂纹扩展或断裂发生前，往往会经历大范围的塑性屈服。弹塑性断裂力学 (EPFM) 正是为处理这类大尺度屈服问题而发展的。在这种情况下，J 积分和裂纹尖端张开位移 (CTOD) 可以作为替代 K 因子的断裂力学参量。

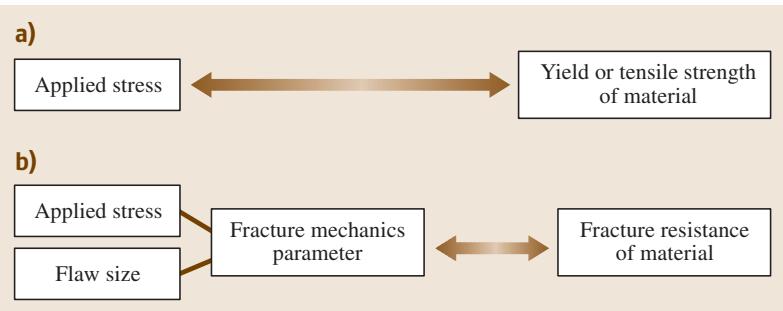
图1 断裂力学设计方法 (b) 与传统设计方法 (a) 的对比

线弹性断裂力学 (LEFM)

设想一个任意形状的弹性体，其内部存在一个理想的尖锐裂纹，并承受任意的外部载荷。如图2所示，裂纹的两个表面存在三种相对运动模式。

• I 型（张开型）：这是工程构件中最常见的位移模式，其特征是裂纹面在主载荷方向上发生张开位移。
• II 型（滑开型）：对应于面内剪切载荷。
• III 型（撕开型）：对应于面外剪切载荷。

在任何实际问题中，含裂纹体都可以看作是这三种模式的一种或组合。

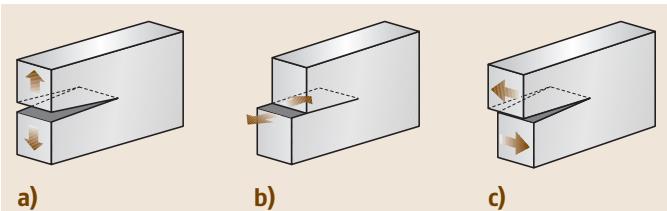
图2 三种裂纹变形模式。(a) I型（张开型） (b) II型（滑开型） © III型（撕开型）

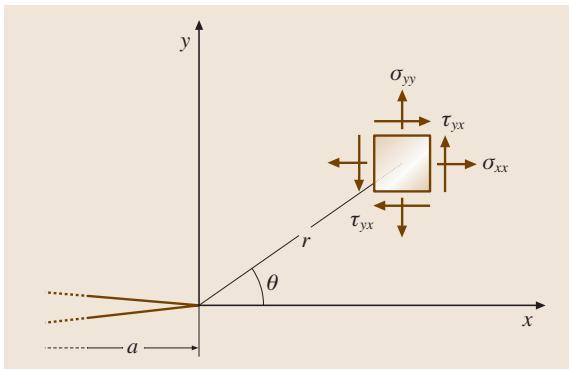
图3 极坐标系下的裂纹尖端应力

基于各向同性线弹性材料的假设，弹性力学理论为每种变形模式都推导出了裂纹尖端周围应力场的封闭解。对于图3所示的极坐标系，任何裂纹体中的应力场可由下式给出：

σ_ij(r,θ) = (k√(a/r))f_ij(θ) + Σ A_n(√(r/a))ⁿ g_ij,n(θ)

其中，σ_ij 是应力张量，k 和 A_n 是常数，f_ij 和 g_ij 是 θ 的函数。式中的高阶项取决于几何边界条件。当 r 趋近于 0 时，第一项（即主导项）趋于无穷大，而其他项则保持有限。因此，无论含裂纹体的具体构型如何，裂纹尖端区域的应力都具有 1/√r 的奇异性。在裂纹尖端前方，当 r 远小于裂纹长度 a 时，应力场可以简化为：

σ_ij,I = [K_I / √(2πr)] f_ij,I(θ)

σ_ij,II = [K_II / √(2πr)] f_ij,II(θ)

σ_ij,III = [K_III / √(2πr)] f_ij,III(θ)

这些场方程表明，弹性应力场的大小可以由单一参量 K_I、K_II 和 K_III 来描述。这个参量就是应力强度因子 K，其下标表示裂纹的变形模式。K 是外加载荷、裂纹形状与尺寸以及结构构型的函数。由于 I 型裂纹在实际工程结构中最为普遍和关键，通常在讨论 I 型问题时会省略下标 I。

应力强度因子的一般形式为：

K = Fσ√(πa)

式中，F 是一个取决于带裂纹试样或构件几何形状的参数。对于一个承受均匀拉应力 σ、包含一个长度为 2a 的穿透裂纹的无限大平板，其应力强度因子为：

K = σ√(πa)

上述方程描述了理想化裂纹模型中，裂纹前方奇异区内的弹性应力场。在真实材料中，裂纹尖端的应力并不会达到无穷大，因为裂纹尖端半径必然是有限的，并且该区域的金属材料会发生塑性变形，从而进一步缓和裂纹尖端的应力。但是，在小尺度屈服 (small-scale yielding) 条件下，围绕裂纹尖端的塑性区尺寸与奇异区相比非常小，以至于外围区域的应力分布仍然遵循上述应力场方程的形式。因此，即便裂纹尖端的真实应力被“黑箱”化，应力强度因子 K 仍然是表征裂纹尖端应力场的有效代表性参量。

ASTM 标准给出了小尺度屈服的适用条件：

a ≥ 2.5 (K/σ_ys)²

这个公式构成了线弹性断裂力学的主要局限性之一。

弹塑性断裂力学 (EPFM)

当上述小尺度屈服条件不满足，即进入大尺度屈服状态时，应力强度因子 K 失去了其作为断裂力学参量的物理基础。此时，需要引入新的方法。

J 积分

对于非线性弹性材料，J 积分是一个有效的替代参量。Rice 提出了一个针对裂纹体的路径无关环路积分，即 J 积分，其定义如下：

J = ∫_Γ [W(ε_ij)dy - T_i(∂u_i/∂x)ds]

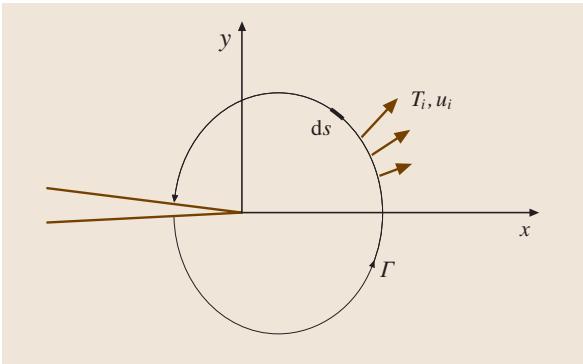
图4 围绕裂纹尖端的环路积分

其中，W(ε_ij) 是应变能密度，T_i 是牵引力矢量分量，u_i 是位移矢量分量，ds 是沿积分路径 Γ (如图4) 的长度增量。

J 积分的值与积分路径无关，对于非线性弹性材料，它等效于能量释放率。研究表明，J 积分不仅能像 K 因子在线弹性材料中那样表征裂纹尖端应力场，还能表征非线性弹性材料中的裂纹尖端应力场（即 Hutchinson-Rice-Rosengren 或 HRR 场）。在大尺度屈服条件下，HRR 场的尺寸取决于塑性屈服的规模和试样的塑性约束。HRR 场是否存在，也构成了 J 积分方法在大尺度屈服应用中的一个限制条件。

裂纹尖端张开位移 (CTOD)

弹塑性断裂力学中的另一个重要参量是裂纹尖端张开位移 (Crack-Tip Opening Displacement, CTOD)。如图5所示，塑性变形会使原本尖锐的裂纹发生钝化。Wells 提出将裂纹尖端的张开量作为衡量断裂韧性的一种度量。

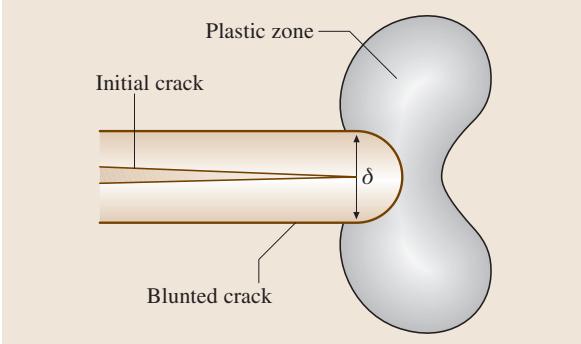
图5 裂纹尖端钝化与CTOD示意图

在小尺度屈服条件下，CTOD (记为 δ) 可以与应力强度因子 K 和 J 积分关联起来：

J = mδσ_ys = K² / E(1 - ν²)

其中，m 是一个取决于材料性能和应力三轴度的无量纲常数，E 和 ν 分别是弹性模量和泊松比。

对 J 积分和 CTOD 的评估存在实际困难。根据 J 积分的定义式进行计算，需要基于材料的本构方程（塑性应变与应力的关系）进行数值分析。而 CTOD 在数值分析中的定义也存在一定的模糊性。因此，在实际结构中应用弹塑性断裂力学并评估这些参量是相当复杂的。幸运的是，对于深裂纹弯曲试样，目前已经提出了一些简化的实验程序来评估 J 积分和 CTOD。

对J积分和CTOD的精确评估，往往需要复杂的数值分析和严格遵循的实验规程，这对于确保结构安全评估的可靠性至关重要。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测材料断裂韧性评估，可靠准确。欢迎沟通交流，电话19939716636