材料缺陷的波谱学表征：从驰豫到共振的深度解析

在材料科学与工程领域，缺陷的存在，尤其是点缺陷、杂质及其团簇，深刻地影响着材料的力学、电学、光学及磁学性能。因此，能够精确、灵敏地探测并表征这些微观尺度上的不完美结构，对于材料的性能优化、失效分析以及新材料的开发至关重要。本文将系统梳理一系列先进的波谱学表征方法，深入探讨它们如何从不同物理维度——如机械响应、振动模式、电子跃迁、自旋状态及核相互作用——揭示材料内部的缺陷信息。

一、 驰豫谱学 (Relaxation Spectroscopy)

驰豫现象描述了系统在受到外部扰动后，如何随时间恢复到平衡态的过程。通过分析这一过程的特征时间与强度，可以获取关于缺陷动力学与浓度的宝贵信息。

1.1 机械谱学 (Mechanical Spectroscopy)

当缺陷或杂质在晶格中引发各向异性的畸变时（如图1a所示的应变椭球），外加应力会诱导这些畸变中心发生取向有序化。这一过程可以通过机械损耗峰，即斯诺克（Snoek）驰豫峰来探测。通过分析该峰，可以评估λ张量（描述畸变各向异性）和驰豫时间。其平衡非弹性应变 ε_a^(eq) 可由下式给出：

$$ /epsilon_{/mathrm{a}}^{/mathrm{(eq)}} = /frac{C_0v_0/sigma}{3kT}/left[/sum_p/left(/lambda^{(p)}/right)^2 -/frac{1}{3}/left(/sum_p/lambda^{(p)}/right)^2/right] $$

其中， $$ /lambda^{(p)} = (/alpha_{1}^{(p)})^{2}/lambda_{1} + (/alpha_{2}^{(p)})^{2}/lambda_{2} + (/alpha_{3}^{(p)})^{2}/lambda_{3} $$

这里，C₀ 是各向异性畸变中心的浓度，v₀ 是摩尔体积，而 α₁^(p), α₂^(p), α₃^(p) 是应力轴与λ张量三个主轴之间的方向余弦。一个典型的应用场景是研究体心立方（bcc）金属中的碳、氮、氧等间隙原子。这些原子占据三个等效的八面体间隙位置之一，从而在不同晶向引起四方畸变。斯诺克驰豫的概念也被应用于非晶合金中的氢致内耗峰研究。

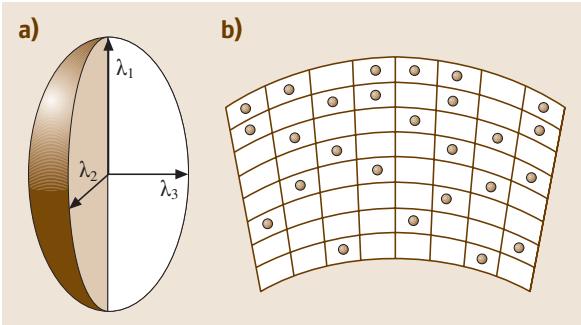图1 (a) 应变椭球；(b) 弯曲试样中的氢原子

当固溶体中尺寸不同的溶质原子对以最近邻方式排布时，它们也能构成各向异性畸变中心。在这种情况下，与应力诱导的畸变中心再取向相关的非弹性驰豫峰被称为齐纳（Zener）驰豫。齐纳驰豫提供了一种无需放射性同位素，在远低于常规扩散方法所需的温度下，研究置换式合金中原子迁移的有效工具。

如果外加应力引起的晶格畸变并非均匀分布，间隙杂质会发生应力诱导的再分布，从而产生非弹性应变（如图1b所示）。这种驰豫被称为戈斯基（Gorsky）驰豫，它为研究间隙杂质的长程迁移提供了强有力的手段。

对于矩形截面试样，戈斯基驰豫的驰豫时间 τ 和驰豫强度 Δ_E 分别为：

$$ /tau = d^2 //pi^2 D $$ $$ /Delta_{E} = (C_{0}v_{0}E / 9kT/beta)(/mathrm{tr}/lambda)^{2} $$

式中，D 是杂质的扩散系数，β 是每个主晶格原子对应的间隙位置数，d 和 E 分别是试样的厚度和杨氏模量。由于氢具有极高的扩散速率，该方法常用于氢扩散研究。

1.2 介电或磁弛豫

在缺陷和杂质的介电或磁响应中，也存在着非常相似的驰豫过程。例如，在碱金属卤化物中，F_A 心（由一个阴离子空位和一个等价阳离子杂质原子构成的对）这类紧密束缚的离子对，其电偶极矩方向沿键轴方向。当施加或撤去电场时，电偶极矩会通过组成原子的移动发生再取向，这一过程表现为介电驰豫。同样，点缺陷和杂质的移动也会引起磁后效。由于体心立方金属中的间隙原子会通过磁致伸缩响应外部磁场而扩散，其机理与斯诺克效应本质上相同，因此斯诺克驰豫也可以通过测量磁弛豫来进行研究。

1.3 噪声谱学 (Noise Spectroscopy)

驰豫与涨落是物理量 q 在随机力作用下统计行为的两个侧面。由时间常数 τ_r 表征的德拜型驰豫行为，描述了物理量对阶跃激励的响应，其自相关函数为：

$$ /phi_{q}(/tau) = /langle q(t)q(t + /tau)/rangle /propto /exp (-/tau //tau_{/mathrm{T}}) $$

根据维纳-辛钦定理，时域中的自相关函数与频域中的涨落功率谱 S_q(ω) 相关联：

$$ S_{q}(/omega) = 4/int_{0}^{/infty}/phi_{q}(/tau)/cos /omega /tau /mathrm{d}/tau $$

因此，通过测量系统在无外部激励下的涨落功率谱（即噪声），我们就能推断出驰豫时间。这些涨落可以以电噪声的形式被探测到。噪声的来源因情况而异。在含有杂质或缺陷（在带隙中形成深能级）的半导体中，可以观察到产生-复合（g-r）噪声，它源于载流子在深能级和导带/价带之间随机交换所引起的载流子密度涨落。由于涨落或驰豫时间常数通常由载流子从深能级到能带的热激发速率决定，测量噪声强度随温度的变化，便可提供关于深能级相对于相关能带边深度的谱学信息。当载流子数量减少时，这种噪声会变得更加显著，因此噪声谱学对于研究纳米结构等小型系统非常有用。

二、 光学与振动光谱

这类方法通过探测材料与光子的相互作用，揭示与缺陷相关的局域振动模式和电子结构信息。

2.1 红外吸收光谱 (IRAS)

红外吸收光谱探测的光子能量由原子质量及周围化学键的强度决定。因此，当杂质原子质量与基体原子相近时，其局域振动频率很容易与晶格声子谱带重叠，形成共振模式，由于强烈的背景信号而难以在IRAS中被检测。与本征点缺陷相关的局域振动模式（LVM）也存在类似问题，加之简单的本征点缺陷易于形成复合物，因此关于本征点缺陷LVM的IRAS研究报道甚少。

相比之下，对轻元素（如硅中的氧）的IRAS研究则非常深入，并积累了大量实验数据。氢是一种极轻的元素，它常被用作间接探针，通过与氢-缺陷复合物相关的LVM来探测点缺陷，例如硅中的自填隙原子和空位。IRAS对杂质的探测极限约为0.01%。

2.2 拉曼光谱 (Raman Spectroscopy)

拉曼散射是一个双光子过程，其散射信号通常非常微弱。因此，常规拉曼光谱很少用于研究低密度缺陷相关的局域振动。然而，当采用共振拉曼散射技术时，在荧光或发光背景较低的理想条件下，探测极限可降至ppb（十亿分之一）量级。图2展示了共振拉曼散射的强大能力，它成功探测到了低温生长的砷化镓（GaAs）晶体中与砷相关点缺陷的LVM。

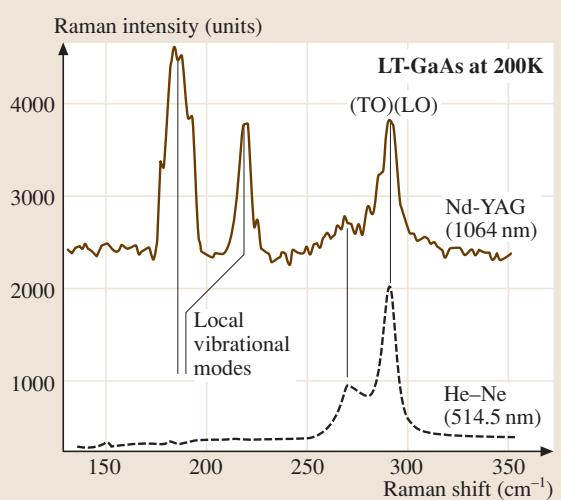图2 在200K下使用两种不同激发激光器测量的低温生长GaAs晶体的缺陷选择性共振拉曼光谱。Nd:YAG激光器（1064nm）的波长与As相关的EL2中心的内部电子激发共振。（承蒙A. Hida博士惠赠）

要使LVM能被拉曼散射清晰地探测到，其振动能量必须与强度较大的共振模式（与晶格声子谱带共振的局域模式）的能量有明显的分离。碘化钾（KI）中的F-心（捕获一个电子的中性阴离子空位）是一个特例。由于钾和碘的质量差异巨大，其声学和光学声子谱带之间的禁带足够宽，可以容纳由缺陷诱导的带隙模式。

2.3 可见光吸收与光致发光 (PL)

与IRAS和拉曼光谱不同，可见光至近红外区的光吸收和光致发光（PL）被广泛用于研究非金属固体中的缺陷。如果样品能产生强烈的PL信号，其灵敏度可高达约0.1 ppm。PL谱与光吸收谱互为补充，两者都反映了电子偶极跃迁。

半导体和绝缘体中的缺陷常常在带隙中引入电子态，碱金属卤化物中的色心是其经典范例。当电子态深埋于带隙中时，电子波函数趋于空间局域化。此时，电子能量对缺陷局域的原子排布非常敏感，这种效应被称为强电子-晶格耦合。耦合的强度直接反映在光学跃迁谱上。图3通过位形坐标图对此进行了说明：每条曲线代表系统的（绝热）势能，是电子能量与原子核势能之和，并表示为原子核位置的一维坐标（位形坐标）的函数。

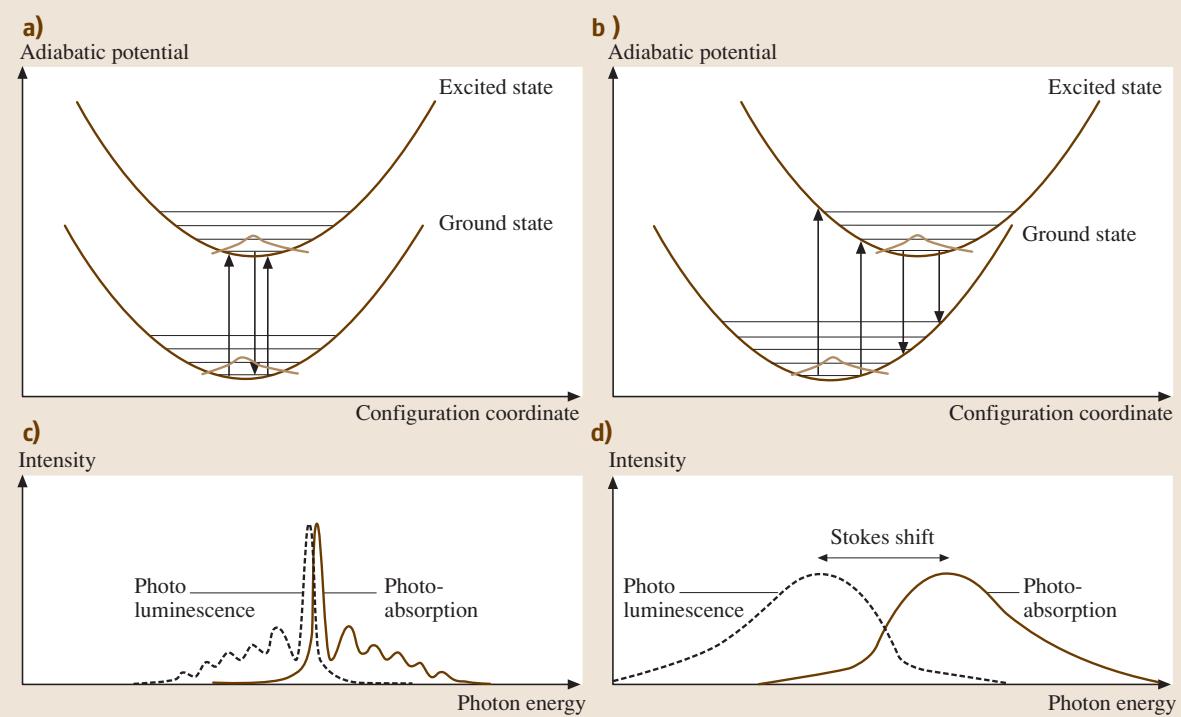图3 (a, c) 弱电子-晶格耦合与 (b, d) 强电子-晶格耦合两种情况下的位形坐标图及对应的光吸收和光致发光(PL)光谱。注意，无论电子-晶格耦合强度如何，吸收光谱和PL光谱几乎呈镜像对称。

• 弱电子-晶格耦合 (图3a)：基态和激发态的稳定构型相差不大。此时，光学跃迁谱的特征是存在一个尖锐的零声子线（图3c），反映了没有声子参与的跃迁。
• 强电子-晶格耦合 (图3b)：基态和激发态的稳定构型差异显著。其结果是谱带展宽，并出现较大的斯托克斯位移（红移），如图3d所示。

通常，偶极光学跃迁的效率会受到各种非辐射过程的竞争，如俄歇过程、多声子发射过程以及热激活开启不同复合通道等。尤其是最后一种过程在许多体系中都很普遍，因此PL测量样品通常需要冷却到低温（≤ 20K）以获得可探测的PL强度。样品冷却也有助于在光吸收和PL测量中分辨出精细的光谱结构。

利用阴极发光（CL）作为信号的扫描电子显微镜（SEM-CL）可以观察半导体晶体中发光中心的分布。图4展示了半导体量子点的单色SEM-CL图像，从中可以确定每种发光分别源于量子点的哪个区域。配备了光收集系统的扫描透射电子显微镜（STEM）也能获得类似的图像，其优势在于还能同时获取缺陷的晶体学信息。

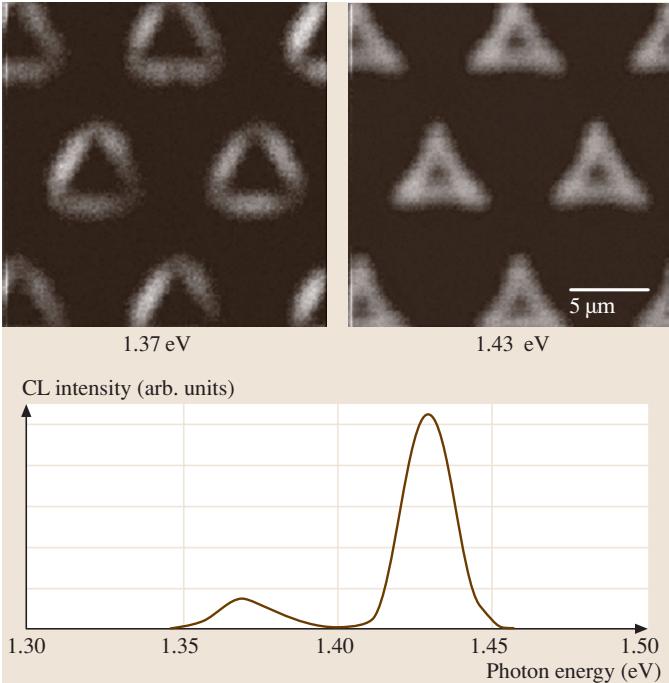图4 半导体量子点的单色SEM-CL图像及其CL光谱

三、 磁共振波谱

磁共振技术通过探测样品中电子或原子核的自旋在磁场中的行为，提供关于缺陷周围局域化学环境、对称性和电子结构等极其精细的信息。

3.1 电子顺磁共振 (EPR)

在顺磁性物质中，由于不存在交换相互作用，与电子顺磁共振（EPR）相关的有效自旋哈密顿量为：

$$ H = B_{0}/gamma_{/mathrm{e}}^{/prime}S - /lambda^{2}S/Lambda S + S/Lambda I $$

这里，静态磁场 B₀ 会引起未成对电子的塞曼分裂，其分裂能量远大于核自旋的塞曼分裂。当微波频率与拉莫尔频率共振时，便可观察到可测量的微波吸收。与傅里叶变换核磁共振（FT-NMR）不同，EPR谱是通过扫描施加于微波谐振腔（频率固定，约10 GHz）内样品的外磁场来测量的。信号通常采用磁场调制技术进行探测，共振场可以精确地确定为信号穿过零基线的位置（图5a）。

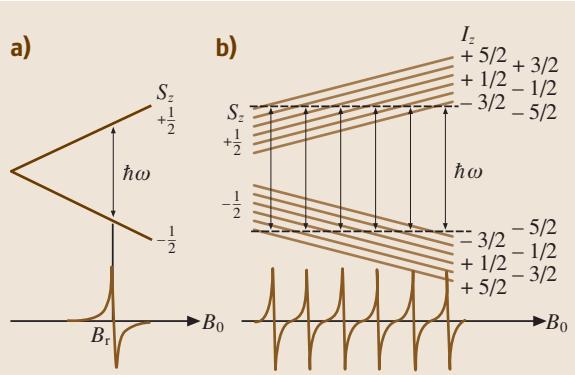图5 (a) 孤立电子的自旋共振信号；(b) 电子与一个核自旋I = 5/2的原子核发生超精细相互作用时的信号。

通过分析电子 g 张量或相应共振场随晶轴相对于外磁场方向的变化，可以确定缺陷的对称性。半导体中的某些点缺陷会在带隙中形成能级，并根据费米能级的位置改变其电荷态。如果由于中心的点对称性导致轨道能级简并，那么根据电荷态的不同，可能会发生对称性破缺的晶格畸变（姜-泰勒畸变），从而解除简并并降低电子能量。EPR方法在确定不同电荷态下硅中空位的结构方面展现了其强大威力，这是一个历史性的例子。

通过分析源于哈密顿量最后一项 SAI（电子自旋与核自旋间的磁偶极-偶极相互作用）的超精细结构，可以识别中心的化学环境或缺陷的晶格位置。以离子晶体MgO中的氧空位为例（图6）。O^-2 离子的空位带双正电荷，所有电子成对，因此对EPR不敏感。但如果它捕获一个电子变为单正电荷，未成对的 S = 1/2 自旋就会产生EPR信号。

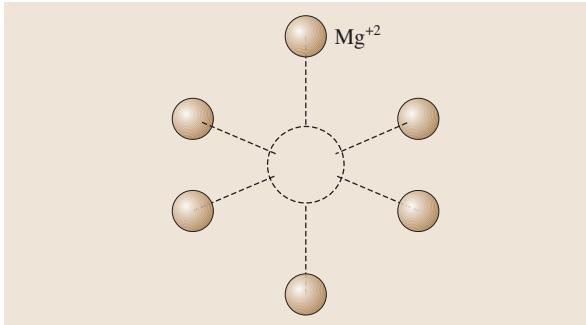图6 MgO中的氧空位

由于空位中心没有原子核，超精细相互作用仅来自于周围六个等距的 Mg²⁺ 离子。在镁的同位素中，只有 ²⁵Mg（丰度10.11%）具有非零核自旋 I = 5/2。因此，超精细信号的相对强度由 ²⁵Mg 离子占据六个 Mg 离子位置的概率决定。例如，所有六个位置均不被 ²⁵Mg 占据的概率为 (0.8989)⁶ = 52%，因此52%的空位不显示超精细分裂（如图5a）。类似地，邻近有一个 ²⁵Mg 离子 (I = 5/2) 的概率为 6 × (0.8989)⁵ × (0.1011) = 35.6%，因此35.6%的空位应展现出 (2I + 1) = 6 条超精细分裂信号（如图5b）。找到两个 ²⁵Mg 离子的概率约为10%，会展现出11条超精细分裂信号，其强度比为1:2:3:4:5:6:5:4:3:2:1，这已得到实验验证。

电子-核相互作用可以扩展到包含与次近邻原子核的间接相互作用，从而在每条超精细信号周围产生超超精细结构。EPR谱学的一个主要缺点是分辨率较低（Δν ≈ 10 MHz），远低于NMR（Δν ≈ 50 kHz），这在分析拥挤或重叠的信号时是个劣势。为了克服这个问题，发展出了**电子核双共振（ENDOR）**技术（图7）。当对引起超超精细结构的原子核施加核磁共振时，EPR信号强度会发生变化。ENDOR不仅提高了常规NMR的灵敏度，还被用于研究EPR探测到的电子云的空间范围。

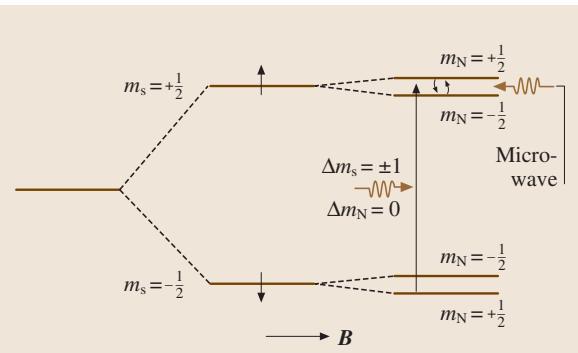图7 I = 1/2原子核的电子核双共振（ENDOR）

在半导体中，只要自由载流子密度低于 10¹⁸ cm^-3，使得微波能良好穿透样品，EPR可以探测到稀疏至 10¹⁴ 到 10¹⁶ cm^-3 的未成对自旋。在金属中，自由电子的存在会因趋肤效应而限制微波的穿透深度。必须强调，只有存在未成对电子时才能探测到EPR信号。

3.2 光探测磁共振 (ODMR)

光探测磁共振（ODMR）是一种双共振技术，适用于研究磁场能够解除自旋简并的电子态。它能实现高灵敏度的EPR测量，并有助于指认与磁共振相关的自旋态。最常见的实验方案是探测响应磁共振而变化的圆偏振光致发光（PL）或磁圆二色吸收（MCDA）。

如图8所示，当施加静磁场时，原本自旋简并的基态和激发态分裂成塞曼能级。根据选择定则，光学跃迁在特定自旋能级间发生，并产生特定偏振光。如果在激发态的塞曼能级间施加共振电磁波，会改变能级布居，进而改变出射光的偏振特性。通过监测这种变化，即可探测到激发态的EPR。这种基于PL探测的磁共振，或称磁圆偏振发射（MCPE），只要PL强度足够高，其灵敏度可以超过普通EPR。

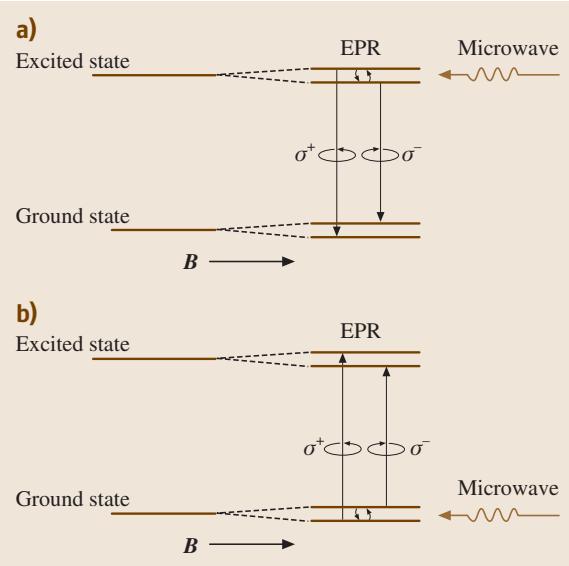图8 (a) 磁圆偏振发射（MCPE）和 (b) 磁圆二色吸收（MCDA）

类似地，基于MCDA的ODMR（图8b）则有助于指认基态的自旋。MCDA的优势在于它适用于不发光的样品。其他用于ODMR的信号还包括自旋翻转拉曼散射光、受缺陷中心自旋态影响的电流共振变化等。特别是电探测磁共振（EDMR）技术，能够选择性地探测位于狭窄电流路径上的极少数顺磁中心。

四、 基于核与粒子探测的谱学方法

这类技术利用特殊的探针粒子（如μ子、正电子）或放射性原子核与材料相互作用，从原子核的视角探测其周围的局域场环境和缺陷状态。这些方法往往需要大型科研设施，但能提供独特的、其他技术难以获得的信息。

4.1 μ子自旋旋转 (μ⁺SR)

μ子是一种介子，由高能粒子加速器产生。它是一种自旋为1/2的费米子，质量约为电子的207倍。带正电的μ⁺子在固体中会被原子核排斥，因此它会沿着间隙位置迁移或被空位等负电性缺陷捕获，其行为像一个轻质的“质子同位素”。μ⁺子在约2μs的平均寿命内会衰变，并沿其自旋方向发射出具有特征角分布的γ射线（图9a）。通过探测这种γ射线信号随时间的振荡，可以测量μ⁺子在局域磁场中的拉莫尔进动频率（图9b）。

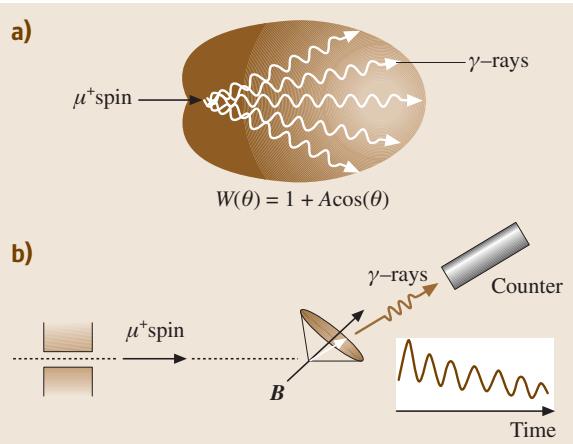图9 (a) 来自μ⁺自旋的γ射线定向发射；(b) μ⁺SR实验装置示意图

在铁磁性固体中，μ⁺子感受到的内磁场对其所处位置（间隙位或空位）高度敏感。通过监测μ⁺SR信号随温度的变化，可以研究高能粒子辐照引入的空位的扩散和回复过程。

4.2 扰动角关联 (PAC)

某些放射性核素（如 ¹¹¹Ag 和 ¹¹¹In）在衰变过程中会相继发射两束γ射线（图10a）。如果中间态的寿命很短（< 数百纳秒），这两束射线之间存在角关联。当存在磁场或电场梯度等外部场扰动时，具有磁矩的中间态原子核自旋会在其寿命期间发生旋转（图10b）。通过符合计数技术测量第二束γ射线相对于第一束的方向变化，可以探测到自旋旋转引起的振荡信号（图10c）。PAC方法与μ⁺SR类似，可用于研究点缺陷的回复过程。

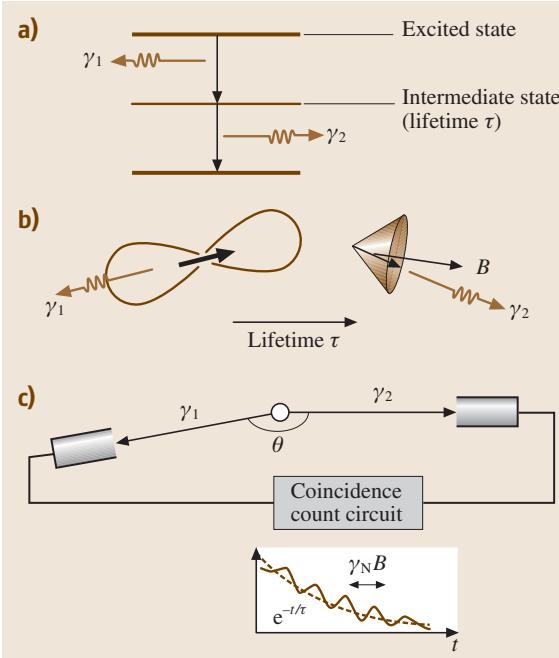图10 (a-c) 在扰动角关联（PAC）实验中，相继发射的两束γ射线的方向(a)指示了中间态核自旋的方向，该自旋可能在内磁场中旋转(b)。自旋旋转通过符合计数电子学探测©。

4.3 固态核磁共振 (Solid-State NMR)

固态NMR的一个著名应用是测量原子的扩散速率。固体中原子核的运动会导致局域磁场的涨落，这种涨落的频率分量若与拉莫尔频率匹配，会引起塞曼能级间的共振跃迁，导致自旋-晶格驰豫时间 T₁ 缩短。当涨落的相关时间 τ 满足 ω_Lτ ≈ 1 时，T₁ 缩短最有效。通过测量 T₁ 随温度的变化，找到 T₁ 达到最小值的温度，结合不同外磁场下的数据，可以绘制阿伦尼乌斯图，从而评估原子跳跃的激活能和指前因子。

4.4 正电子湮没谱 (PAS)

正电子是电子的反粒子，由某些放射性同位素（如 ²²Na）衰变产生（图11）。注入固体后，正电子会迅速热化，并最终与一个电子发生湮没，通常发射出两束能量为0.511 MeV、方向几乎相反的γ射线。

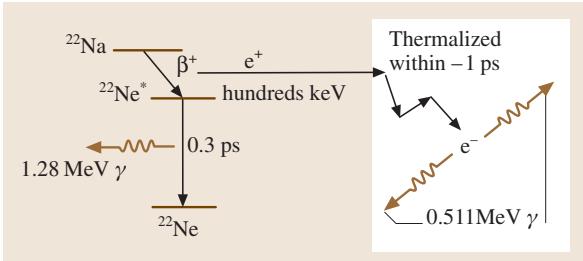图11 正电子的产生及其在固体中与电子的湮没过程

PAS最简单的模式是正电子寿命测量。正电子的寿命反映了其湮没位置的电子密度。由于带正电，正电子极易被空位、微孔洞、位错核心等原子缺失型缺陷捕获。在这些区域，电子密度较低，导致正电子寿命显著延长。图12展示了计算出的不同尺寸空位团簇对应的正电子寿命。通过将实验测得的寿命值与理论预测对比，可以可靠地推断空位的尺寸。PAS对空位的探测极限在金属中可达10^-6量级，比膨胀法高2-3个数量级，并且可以在热平衡下测量，这是其相对于需要淬火的电阻率法的一大优势。

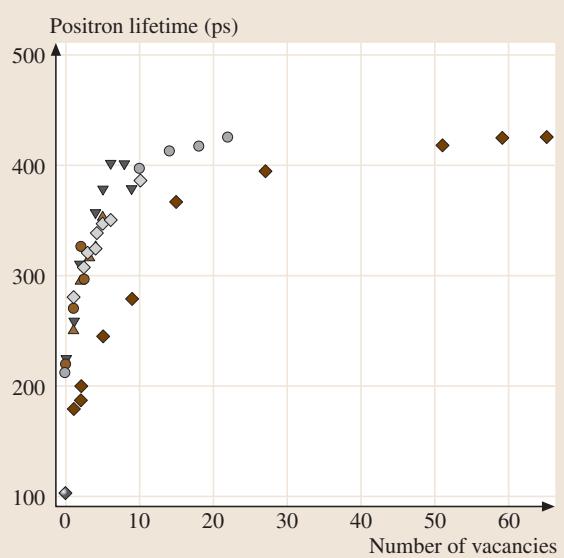图12 计算的不同尺寸空位的正电子寿命。图中包含了Si和Fe的实验与理论数据。（承蒙M. Hasegawa教授惠赠）

γ-γ角关联测量是PAS的另一种形式（图13）。由于湮没前电子具有动量，两束γ射线的发射方向并非完全相反。角关联曲线的形状与湮没处电子的动量分布有关。当正电子被空位型缺陷捕获时，与动量较小的传导电子湮没的比例增加，导致角关联曲线的中心部分变得更尖锐。通过量化曲线形状的变化，可以研究缺陷的演化过程。现代的二维角关联湮没辐射（2D-ACAR）技术，能够研究纳米尺寸的晶相，如贵金属中的G-P区。

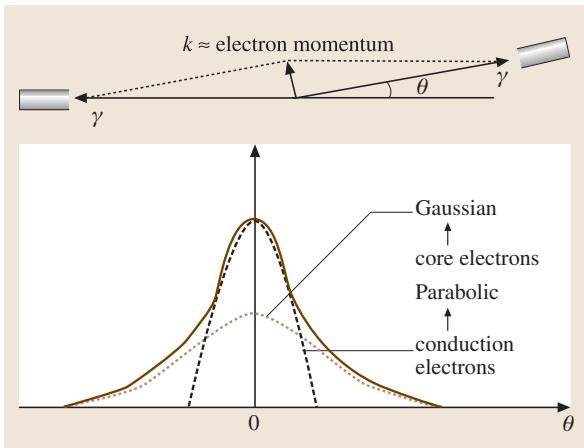图13 γ-γ角关联实验装置及示意性关联谱

利用能量可调的慢正电子束，还可以研究点缺陷的深度分布，这在半导体器件技术中尤为重要。

这些基于粒子探测的先进技术，对于揭示材料深层次的缺陷信息具有不可替代的作用。然而，它们的实施往往依赖于大型、复杂且昂贵的实验设施，对操作人员的专业知识和经验要求极高。这正是专业检测实验室的核心价值所在。 精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），央企，国字头检测机构，专业的权威第三方检测机构，专业检测材料缺陷与微观结构表征，可靠准确。欢迎沟通交流，电话19939716636

4.5 穆斯堡尔谱 (Mössbauer Spectroscopy)

穆斯堡尔谱学基于嵌入固体中的特定原子核（穆斯堡尔核）对γ射线的无反冲共振吸收现象。由于其极窄的自然线宽（约5×10^-9 eV），该技术对原子核所处的局域化学和磁环境极为敏感。实验装置如图14所示，通过多普勒效应精确改变γ射线的能量，扫描样品的吸收光谱。

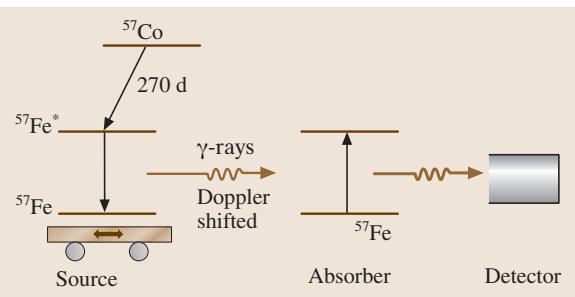图14 穆斯堡尔谱实验装置

穆斯堡尔谱可以测量原子核处的内磁场（通过核塞曼分裂）和电场梯度（通过四极分裂），从而探测铁磁相、晶体场的对称性破缺等。图15展示了淬火钢中铁的穆斯堡尔谱，清晰地分辨出马氏体相和残余的顺磁性奥氏体相。

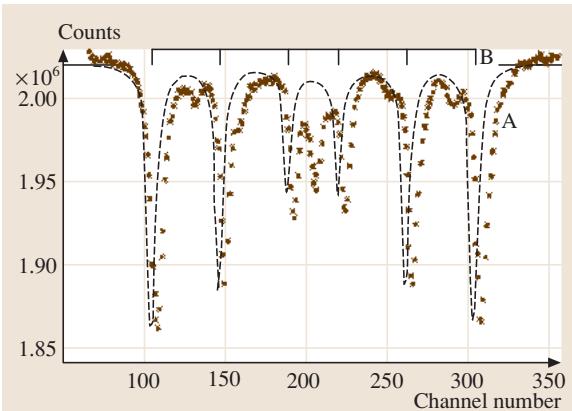图15 铁-4.2%碳马氏体的穆斯堡尔谱(A)与纯α-铁的谱(B)。中心峰来自顺磁性奥氏体相。

五、 深能级瞬态谱 (DLTS)

在半导体领域，点缺陷常在带隙中形成深能级。深能级瞬态谱（DLTS）是一种高灵敏度的电学测量技术，能够定量测量深能级的浓度和能量位置。其原理是：通过电脉冲或光照扰动金属-半导体结耗尽区内深能级的电荷占据状态，然后监测其通过热激发回复到平衡态的过程。这个回复过程通常通过测量结电容的瞬态变化来表征。

回复速率与能级深度和温度直接相关，通过分析电容瞬态信号随温度的变化，可以精确计算出深能级的激活能（即能级深度）和俘获截面。电容变化的总量则对应于缺陷的浓度。DLTS的一个显著优势是，通过电容变化的符号可以明确判断是电子陷阱还是空穴陷阱，从而确定能级深度是相对于导带边还是价带边。在适当掺杂的样品中，DLTS的探测灵敏度可高达约 10¹⁴ cm^-3。