晶面符号（米勒指数）：解码晶体微观世界的通用坐标系

在材料科学与晶体学的领域，我们如何精确描述晶体内部原子排列的特定平面？这并非一个纯粹的几何问题，它直接关系到材料的力学性能、化学活性、光学和电学特性。无论是半导体晶圆的切割，还是催化剂活性位点的研究，亦或是理解金属的滑移系，我们都需要一套统一、无歧义的语言来标记这些晶面。这套语言就是晶面符号，其中，米勒（Miller）指数是当今应用最广泛的体系。

米勒指数的理论基石是“整数定律”（Law of Rational Indices），一个看似简单却极为深刻的观察：任何晶面在晶轴上截取的截距，其系数之比必然是简单的整数比。米勒在1837年巧妙地利用了这一定律，并对其进行了一次数学变换——取截距系数的倒数，从而发展出了一套更为直观和实用的符号系统。

破译米勒指数：从截距到符号

米勒指数的确定过程，本质上是一个“求倒数再整数化”的标准化流程。我们通过一个具体的例子来拆解这个过程。

假设一个晶面在晶格坐标系的 x, y, z 轴上分别截取了 2a, 3b, 6c 的长度，其中 a, b, c 是该晶向上的晶格常数（轴单位）。

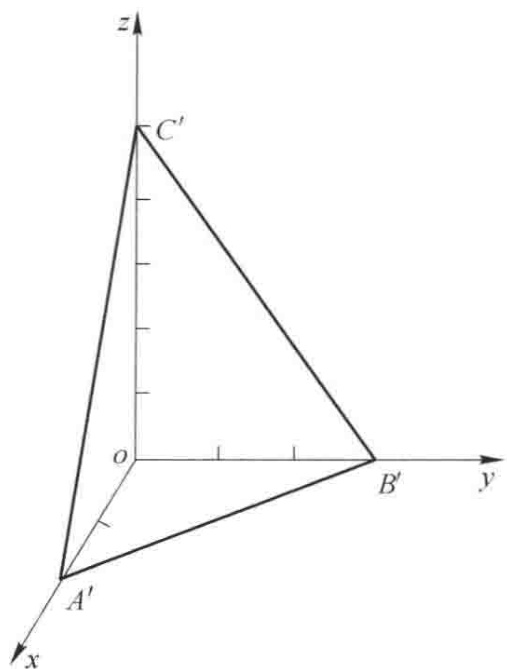
确定该晶面（图1中 A’B’C’）米勒指数的步骤如下：

1. 提取截距系数：晶面在 x, y, z 轴上的截距系数分别为 2, 3, 6。
2. 求取倒数：将这些系数取倒数，得到 1/2 : 1/3 : 1/6。
3. 化为最小整数比：为了消除分数，将各项乘以其最小公倍数 6，得到 3 : 2 : 1。
4. 加括号标记：将这组整数放入小括号中，即得到该晶面的米勒指数 (321)。

括号内的这组数字 (hkl) 称为晶面指数。这里的核心逻辑是：晶面在某个轴上的截距越大，意味着它与该轴的交点离原点越远，其对应的晶面指数就越小。一个极端情况是，如果晶面与某一晶轴平行，可以认为它在该轴上的截距为无穷大 (∞)，其倒数 1/∞ 等于 0。因此，晶面指数中的“0”代表该晶面与对应晶轴平行。

对于不同的晶系，坐标轴的选取有所不同：

• 在立方、四方、正交等大多数晶系中，使用 x, y, z 三轴，晶面指数记为 (hkl)。
• 在三方和六方晶系中，为了更好地体现其对称性，通常引入四个轴 x, y, u, z，其晶面指数记为 (hkil)。其中，i 是一个冗余指数，它与 h 和 k 满足关系 h + k + i = 0。

典型晶体结构的晶面指数

理解了计算方法后，我们来看几个常见晶体形态中各晶面的米勒指数。

等轴晶系：立方体与八面体

等轴晶系（如立方晶系）具有高度的对称性，其晶格常数满足 a = b = c, α = β = γ = 90°。

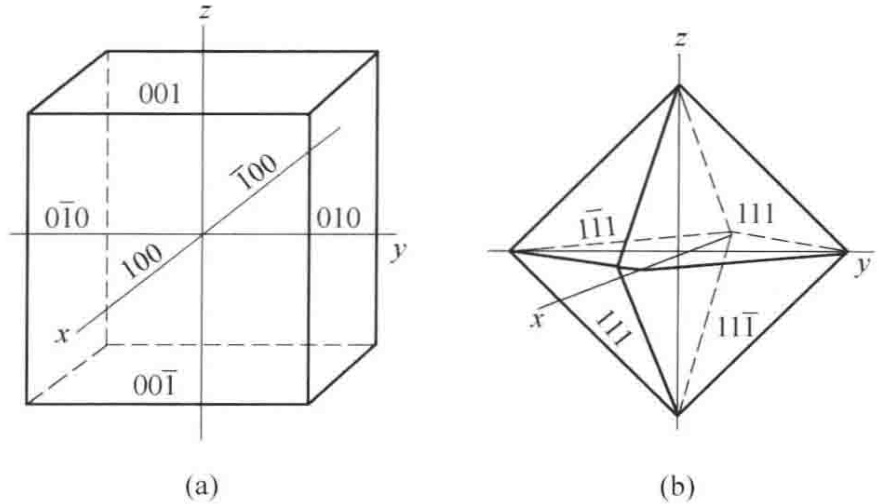
对于一个标准的八面体，其八个面均为 {111} 型晶面。根据其在坐标系中的具体方位，各晶面指数如下表所示。注意，指数上方的横线 ̅ 代表负值。

表1 八面体各晶面符号

准确标定这些晶面指数对于材料的性能分析至关重要。例如，在金刚石或硅这类具有面心立方结构的材料中，(111) 面是其最密排面，也是天然的解理面。精确的晶面取向分析是半导体、光学和精密加工领域质量控制的关键环节。如果您在实际工作中也面临类似的晶体结构分析挑战，我们非常乐意与您一同探讨解决方案。

六方晶系：六方柱

六方晶系的晶格常数特征为 a = b ≠ c, α = β = 90°, γ = 120°。其晶面指数采用四指数的米勒-布拉菲（Miller-Bravais）体系 (hkil)。

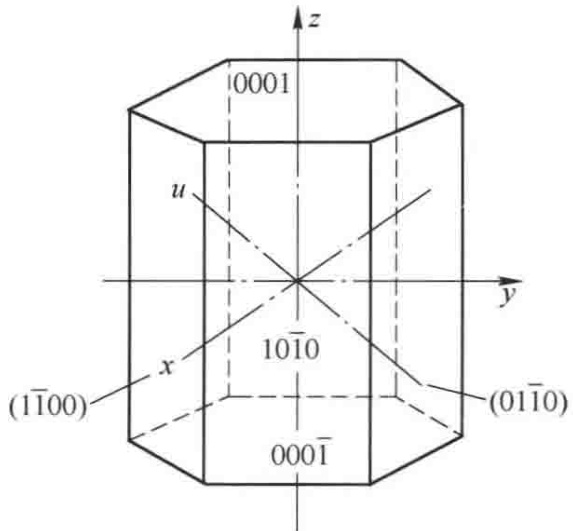
下表列出了一个典型六方柱的主要晶面符号。

表2 六方柱各晶面符号

从理论计算到实际样品表征，确定晶面指数是一个严谨的过程，它要求首先识别晶体的对称性以确定晶系，然后选择符合该晶系规范的晶轴，最后才能进行截距分析。在处理真实材料，尤其是多晶、织构或存在缺陷的样品时，这一过程的复杂性和不确定性大大增加。要获得可靠的晶体取向和结构数据，往往需要借助X射线衍射（XRD）、电子背散射衍射（EBSD）等专业的分析技术。这正是专业检测实验室的核心价值所在。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），专业的权威第三方检测机构，专业检测晶体结构分析央企背景，可靠准确。欢迎沟通交流，电话19939716636