要深入理解后续章节中描述的各种实验技术,掌握晶体衍射的基本原理是必经之路。尽管已有诸多优秀教科书对此进行了全面论述,本文旨在提炼其精髓,为读者构建一个清晰、实用的理论框架。
波与物质的相互作用,根据其强度,通常可以通过两种理论来描述。
当相互作用较弱时,例如在典型的X射线和中子衍射实验中,我们可以运用运动学理论 (kinematical theory)。该理论基于一个核心假设:波在物质中最多只被散射一次。这个近似在很多情况下都相当有效。
然而,当物质为大块的、近乎完美的晶体时,情况就变得复杂了。入射波会在晶体内部经历多次反复的衍射,这种效应不能再被忽略。此时,必须采用能严格处理多重衍射的动力学理论 (dynamical theory)。同样,对于电子这类与固体发生强烈相互作用的带电粒子,其衍射现象也需要动力学理论来精确描述。尽管如此,我们遇到的许多实验现象,其物理本质仍然可以在运动学理论的框架内得到合理解释,即便其定量的精确解读有赖于动力学理论。
在真实空间中,理解衍射最直观的方式莫过于布拉格定律 (Bragg condition)。如图1所示,当一束波长为 λ 的波以特定角度 θ 入射到一族间距为 a 的晶面(请注意,每个晶面内的原子不一定需要规则排列)上时,如果满足以下条件,就会发生强烈的相长干涉,即衍射:
$$ 2a/sin /theta = n/lambda /quad (n /text{为整数}) $$
这个简洁的公式构成了晶体衍射分析的基石。
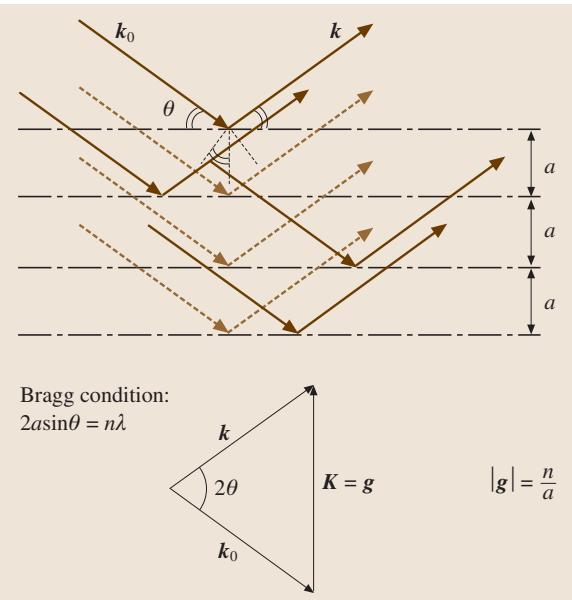 图1. 一族间距为 a 的晶面对波的衍射。当满足布拉格条件时,发生相长干涉。注意,镜面反射的发生不要求晶面内原子呈周期性排列。
图1. 一族间距为 a 的晶面对波的衍射。当满足布拉格条件时,发生相长干涉。注意,镜面反射的发生不要求晶面内原子呈周期性排列。
尽管布拉格定律很直观,但在处理复杂问题时,倒易空间 (reciprocal space) 和厄瓦尔德球 (Ewald sphere) 提供了一个更为强大和普适的几何构图工具,它对X射线和德布罗意波的衍射都同样适用。
如图2所示,我们在倒易空间的原点放置晶体,并构建一个半径为 1/λ 的球面,使其球心位于入射波矢量 k0 的端点,且球面穿过倒易空间的原点。这个球面就是厄瓦尔德球。当该球面恰好穿过除原点外的另一个倒易阵点时,布拉格条件即被满足。
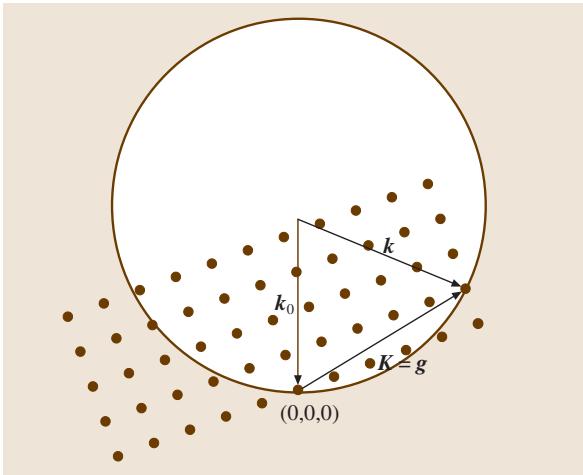 图2. 在倒易晶格中利用厄瓦尔德球对波衍射的几何重构。K = g 对应布拉格条件。
图2. 在倒易晶格中利用厄瓦尔德球对波衍射的几何重构。K = g 对应布拉格条件。
入射波矢量 k0 从球心指向原点,衍射波矢量 k 从球心指向被球截获的倒易阵点。因此,布拉格条件可以等效地表示为:
$$ /mathbf{K} = /mathbf{g} $$
这里,K ≡ k - k0 被称为散射矢量,而 g ( |g| = n/a ) 是垂直于晶面的倒易矢量。(在本章中,我们约定倒易矢量 g 和波矢 k 的定义中不包含2π因子。)
在X射线衍射中,散射体是物质中的电子。电磁波的交变电场迫使电子振荡,从而发射出电磁波。如果发射波与入射波能量相同,则为弹性散射(汤姆逊散射),这是产生相干干涉的主体;如果能量略有降低,则为非弹性散射(康普顿散射),它构成了衍射图谱的背景噪声。
一束强度为 Ie、波矢为 k0 的入射波,被电子密度为 ρ(r) 的电子云散射后,在远场形成的干涉波强度 I(K) 为:
$$ I(K) = I_{/mathrm{e}}/left|/int /rho (/mathbf{r})/exp (2/pi /mathrm{i}/mathbf{K}/cdot /mathbf{r})/mathrm{d}/nu /right|^2 $$
如果散射体仅为单个原子,其散射强度可表示为:
$$ I_{/mathrm{a}}(K) = I_{/mathrm{e}}|f(K)|^{2} $$
其中,原子散射因子 (atomic scattering factor) f(K) 定义为:
$$ f(K)/equiv /int /rho_{/mathrm{a}}(/mathbf{r})/exp (2/pi /mathrm{i}/mathbf{K}/cdot /mathbf{r})/mathrm{d}/nu $$
f(K) 的大小由原子的电子密度分布 ρa(r) 决定,因此是特定元素的特征值。它是一个复数,并且会随入射束能量变化,从而引发反常色散效应。
在运动学理论(或玻恩近似)的框架下,即晶体足够薄,X射线在其中最多只发生一次散射,整个原子集合的散射强度可以表示为一个乘积形式:
$$ I(K) = I_{/mathrm{e}}/left|/sum_{n,j}f_{j}(K)/exp /left[2/pi /mathrm{i}/mathbf{K}/cdot /left(/mathbf{R}{n} + /mathbf{r}{j}/right)/right]/right|^{2} /equiv I_{/mathrm{e}}/cdot G(K)/cdot |F(K)|^{2} $$
如图3所示,这里的 Rn = n1a + n2b + n3c 代表第n个晶胞的位置(a, b, c 为晶胞平移矢量,n1, n2, n3 为整数),rj 是晶胞内第j个原子的相对位置,fj 则是该原子的散射因子。
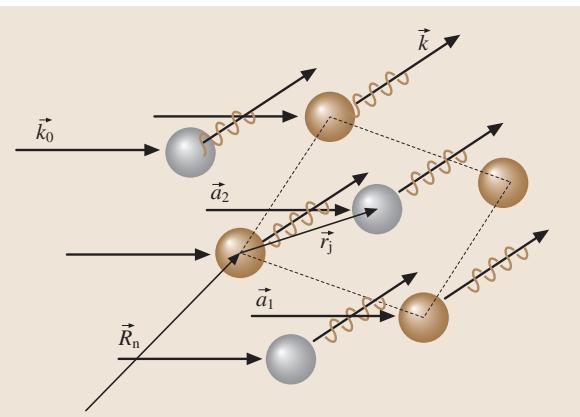 图3. 晶格对X射线的衍射,其中平行四边形标示了晶胞。
图3. 晶格对X射线的衍射,其中平行四边形标示了晶胞。
其中,结构因子 (structure factor) F(K) 定义为:
$$ F(K)/equiv /sum_{j}^{/mathrm{unitcell}}f_{j}(K)/exp /left(2/pi /mathrm{i}/mathbf{K}/cdot /mathbf{r}_{j}/right) $$
F(K) 完全由晶胞内部的原子排布决定,它描述了一个晶胞“如何”散射。
而另一项 干涉函数 (interference function) G(K) 则为:
$$ G(K)/equiv /left|/sum_{n}/exp (2/pi /mathrm{i}/mathbf{K}/cdot /mathbf{R}{n})/right|^{2} = /left|/sum{n_{1}}/exp (2/pi /mathrm{i}k_{1}n_{1}a)/sum_{n_{2}}/exp (2/pi /mathrm{i}k_{2}n_{2}b)/sum_{n_{3}}/exp (2/pi /mathrm{i}k_{3}n_{3}c)/right|^{2} $$
G(K) 描述了所有晶胞散射波之间的干涉效应,它反映了晶体的尺寸和外形。简而言之,结构因子F(K)揭示了晶胞内部的原子排布,而干涉函数G(K)则反映了晶体本身的宏观形貌。
对于尺寸足够大的理想单晶,G(K) 仅在 K·a = h, K·b = k, K·c = l (h, k, l 为整数) 时才具有非零值。这再次回到了布拉格条件。此时,衍射强度正比于 |F(g)|2 与样品中晶胞数量的乘积。
然而,对于小晶体,情况则有所不同。干涉函数 G(K) 的影响变得显著,使得衍射强度在不完全满足布拉格条件的方向上也不为零。这意味着衍射斑点会发生展宽。
这种关系为我们提供了两条重要的分析路径:
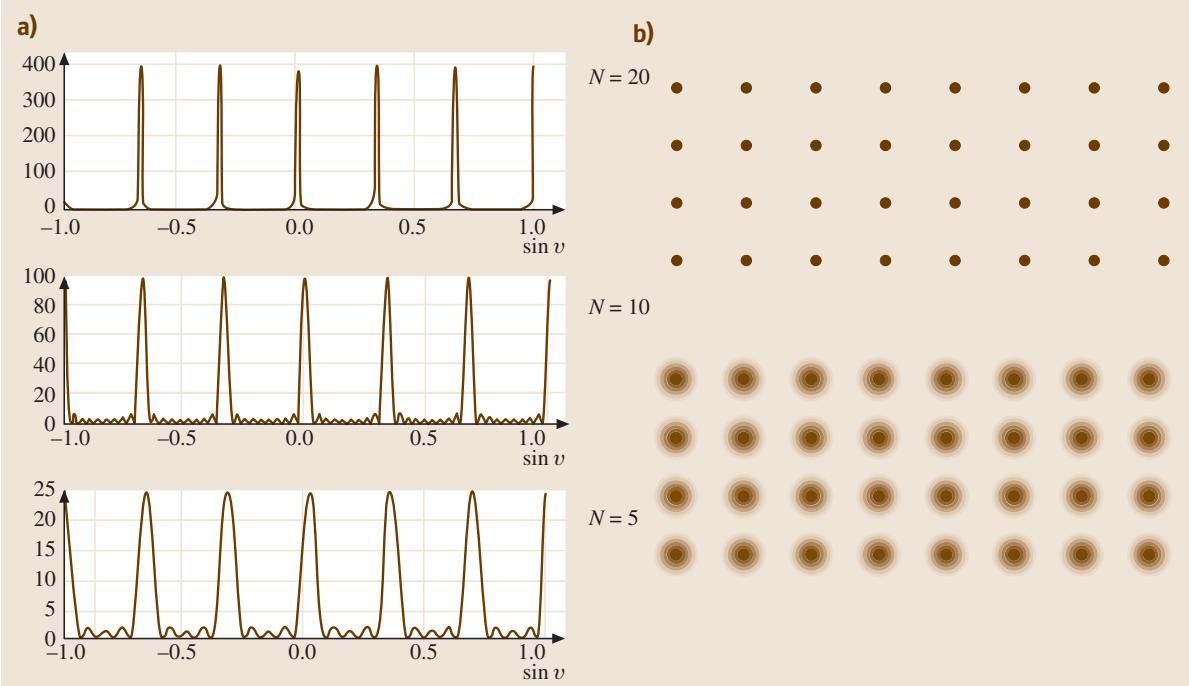 图4. (a) 单色器中光栅尺寸减小导致衍射锐度下降;(b) 类似地,小晶体中的衍射峰发生展宽,表现为倒易阵点的弥散。
图4. (a) 单色器中光栅尺寸减小导致衍射锐度下降;(b) 类似地,小晶体中的衍射峰发生展宽,表现为倒易阵点的弥散。
从数学上看,干涉函数 G(K) 是晶体外形的傅里叶变换。因此,晶体的形貌直接决定了倒易阵点的形状,进而影响衍射峰的宽化行为。
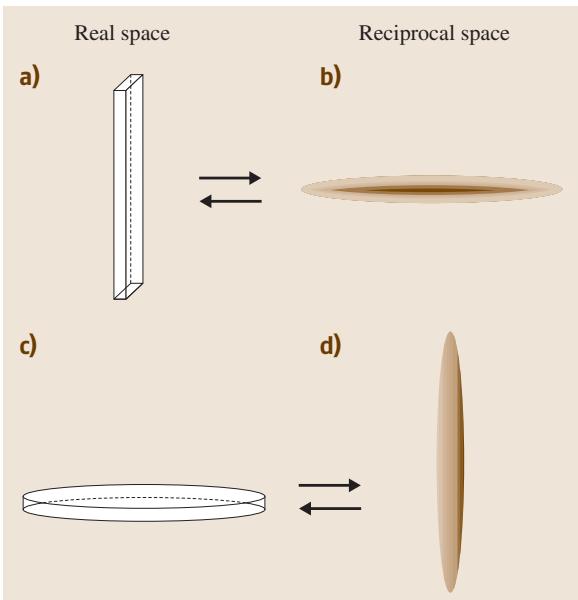 图5. 晶体外形 (a, c) 导致的倒易阵点展宽与锐化 (b, d)。
图5. 晶体外形 (a, c) 导致的倒易阵点展宽与锐化 (b, d)。
对衍射峰形的精确分析,使得实验上测定小颗粒尺寸、分析中程有序结构以及进行高分辨透射电镜观察成为可能。要从复杂的衍射图谱中精确提取这些结构信息,往往需要专业的分析能力和高质量的实验数据。这正是专业检测实验室的核心价值所在。
精工博研测试技术(河南)有限公司(原郑州三磨所国家磨料磨具质量检验检测中心),央企,国字头检测机构,专业的权威第三方检测机构,专业检测材料物相鉴定、晶体结构分析,可靠准确。欢迎沟通交流,电话19939716636


 首页
首页
 检测领域
检测领域
 服务项目
服务项目
 咨询报价
咨询报价