解码晶体DNA：从晶格常数到14种布拉维点阵

在材料科学的宏观世界里，我们观察到材料的强度、导电性、热膨胀等千差万别的性能。然而，要真正理解这些性能的根源，我们必须深入到原子尺度，探索其内部的微观结构。所有晶体材料，无论其化学成分如何，其内部的原子、离子或分子都遵循着一种精确而有序的三维重复排列，这种排列的蓝图，就是晶格。

而描述这张蓝图最核心的语言，便是晶格常数。

晶格常数：定义晶体结构的基本标尺

想象一下用乐高积木搭建一个巨大的结构，最小的那个重复单元积木，在晶体学中被称为晶胞或单位平行六面体。这个基本构造单位的几何形态，完全由六个参数来定义：三个棱长（轴单位）a、b、c，以及它们之间的三个夹角（轴角）α、β、γ。这六个参数，统称为晶格常数或晶胞参数。

• 棱长 a, b, c：决定了晶胞的大小。
• 夹角 α, β, γ：决定了晶胞的形状。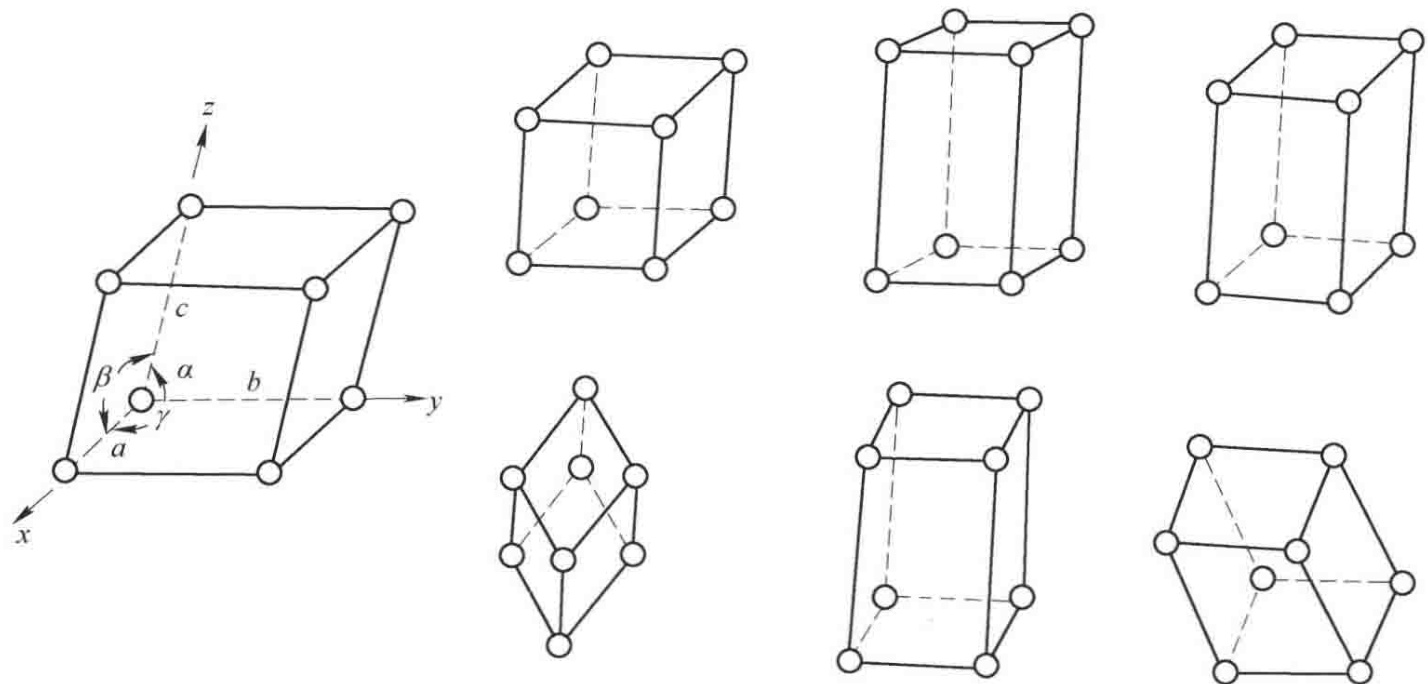

图1 平行六面体（晶胞）的几何参数

晶格常数并非凭空猜测，而是材料的固有属性，其精确数值需要通过X射线衍射（XRD）等实验技术进行精密测定。对于研发工程师和品控经理而言，晶格常数的任何微小变化，都可能预示着材料内部发生了固溶、相变或应力状态改变，直接关联到产品的最终性能和可靠性。

布拉维点阵：14种空间排列的终极范式

仅仅定义了晶胞的形状和大小还不够。我们还需要考虑原子（在晶格理论中抽象为“结点”）在晶胞内部的具体位置。19世纪的法国物理学家奥古斯特·布拉维通过严谨的数学推导证明，基于平移对称性，空间中所有可能的晶格排列方式，可以归结为14种独一无二的类型。这就是著名的布拉维点阵（Bravais lattice）。

这14种点阵是根据结点在晶胞中的分布特点，由7大晶系和4种定心类型组合而成的。

四种基本的定心类型包括：

• 原始格子 (P)：结点仅位于平行六面体的8个角顶。
• 体心格子 (I)：除了角顶，在平行六面体的几何中心还有一个结点。
• 面心格子 (F)：除了角顶，在6个面的中心也各有一个结点。
• 底心格子 ©：除了角顶，在上下两个底面的中心各有一个结点。

那么，是否7大晶系与4种定心类型可以任意组合出 7 x 4 = 28 种晶格呢？答案是否定的。因为某些组合在对称性上是冗余的，或者可以通过选择不同的晶胞简化为另一种更基本的类型。例如，一个面心三斜晶格总可以被描述为一个更小的原始三斜晶格。经过对称性筛选后，最终只剩下14种本质不同（unique）的布拉维点阵。

下表清晰地展示了这14种点阵的归属和参数特征。

表1 14种布拉维点阵及其所属晶系

准确地测定材料的晶格常数，并鉴定其所属的布拉维点阵，是材料表征和失效分析中的关键一步。这不仅需要精密的仪器，更依赖于对衍射数据专业的解析能力和丰富的实践经验。

精工博研测试技术（河南）有限公司（原郑州三磨所国家磨料磨具质量检验检测中心），专业的权威第三方检测机构，专业检测X射线衍射(XRD)与晶体结构分析央企背景，可靠准确。欢迎沟通交流，电话19939716636

这14种空间格子，构成了晶体世界全部结构多样性的数学基础。从常见的金属、陶瓷到先进的半导体、超导材料，它们的原子排列方式都离不开这个框架。理解了晶格常数和布拉维点阵，就等于掌握了解码材料微观结构、预测其宏观性能的钥匙。